圆的对称性（2）

(共16张PPT)
圆的对称性
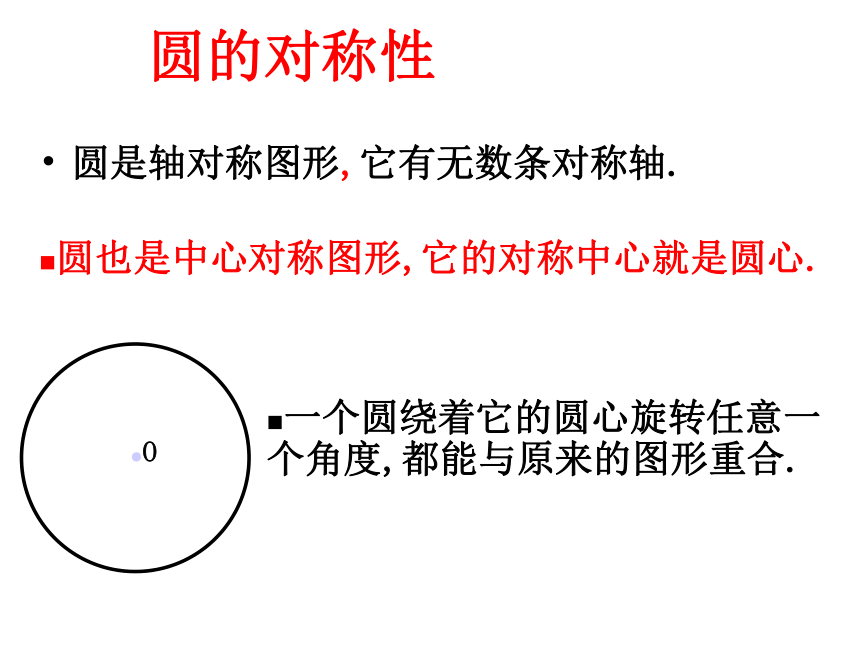
圆是轴对称图形,它有无数条对称轴.
圆也是中心对称图形,它的对称中心就是圆心.
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
●O
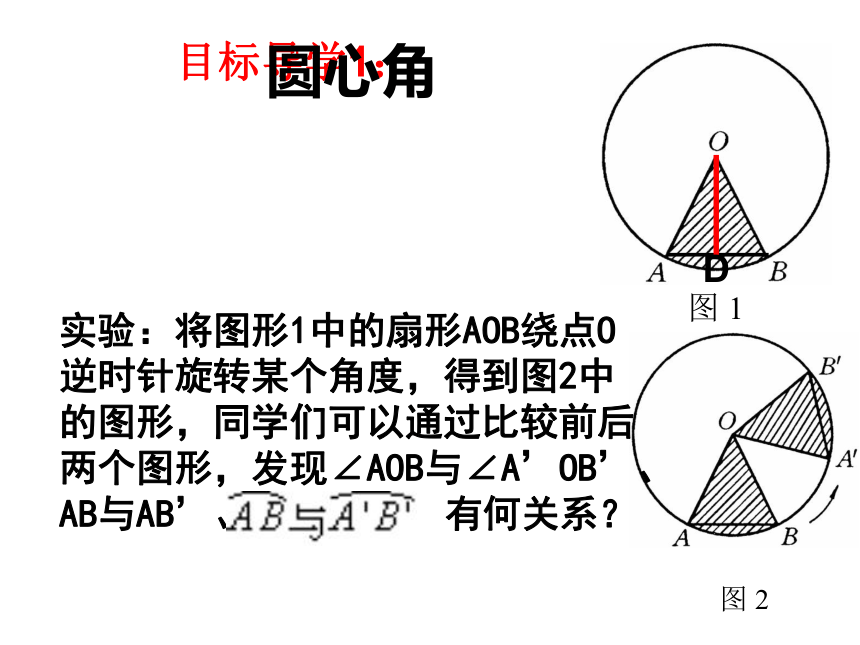
实验：将图形1中的扇形AOB绕点O逆时针旋转某个角度，得到图2中的图形，同学们可以通过比较前后两个图形，发现∠AOB与∠A’OB’、AB与AB’、 有何关系？
目标导学1：
圆心角
D
O
A
B
B
A
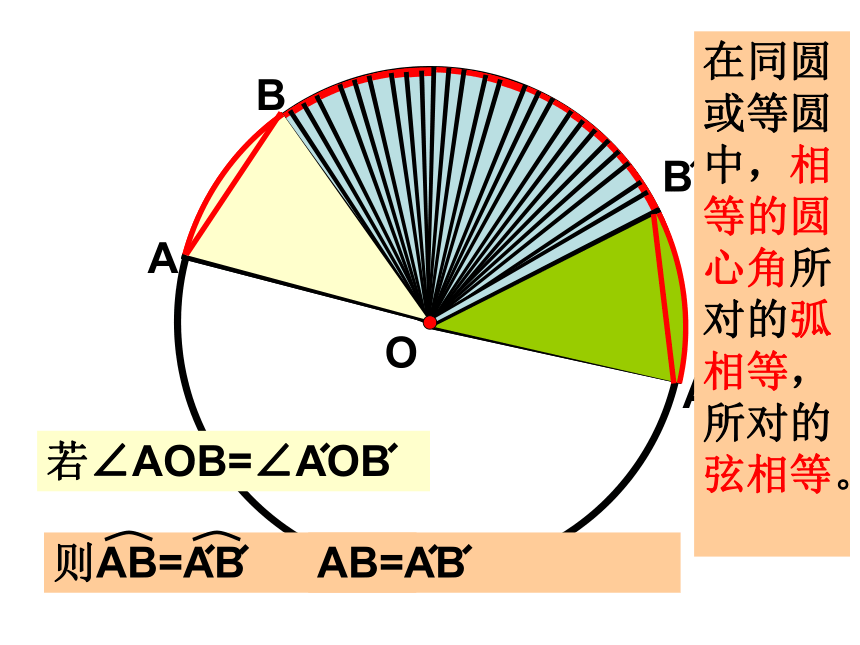
若∠AOB=∠AOB
则AB=AB
AB=AB
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。
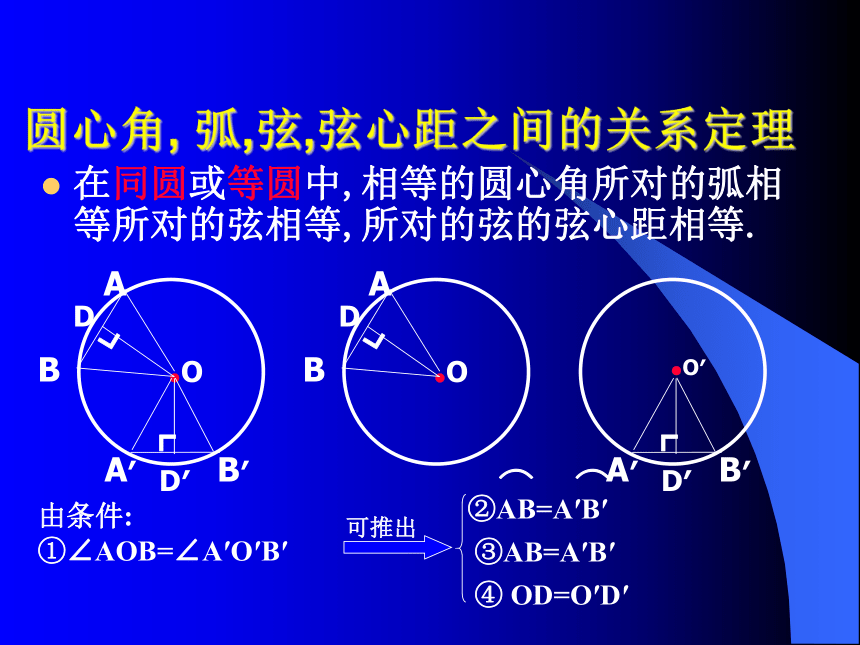
圆心角, 弧,弦,弦心距之间的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
由条件:
①∠AOB=∠A′O′B′
②AB=A′B′
⌒　⌒
③AB=A′B′
④ OD=O′D′
可推出
A
B
O
D
C
E
F
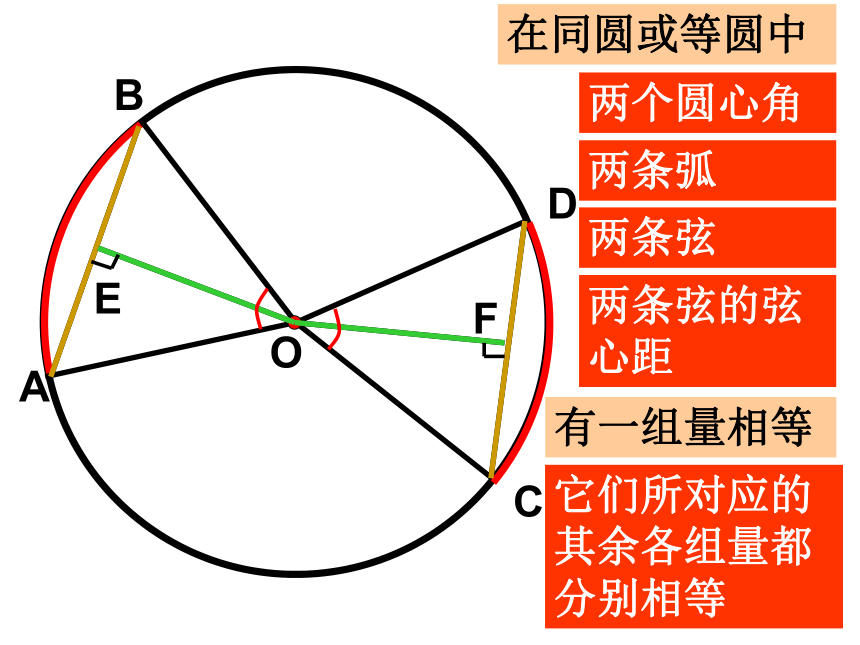
在同圆或等圆中
两个圆心角
两条弧
两条弦
两条弦的弦心距
有一组量相等
它们所对应的其余各组量都分别相等
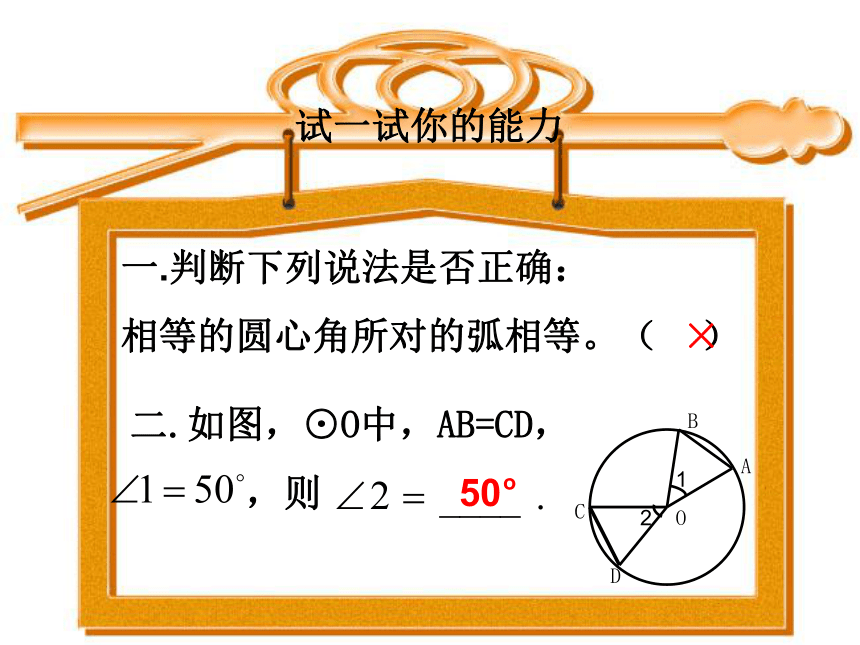
一.判断下列说法是否正确：
相等的圆心角所对的弧相等。（ ）
二.如图，⊙O中，AB=CD，
，则
O
D
C
A
B
1
2
试一试你的能力
×
50
o
1、如图，在⊙O中，弧AB＝弧AC，∠B＝70°.求∠C 度数.
你会做吗？
2、如图，AB是直径，
BC＝CD＝DE，∠BOC＝40°
则∠AOE= 。
1、已知A、B是⊙O上的两点，∠AOB=120°，
C是弧AB的中点，试确定四边形OACB的形
状，并说明理由。
2、在平行四边形ABCD中，以A为圆心，AB长为半径的圆分别交AD、BC于F、G，交BA的延长线于E，求证：EF=FG
O
P
A
B
C
D
例：如图，P是⊙O外一点，射线PAB，PCD分别交⊙O于A、B和C、D，已知AB=CD，
求证：PO平分∠BPD
F
E

3、思考题
已知：在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F，OE、OF的延长线交大圆于AB。
求证：AC＝DB
。O
C
A
E
B
D
F
M
1
2
3
4

3、思考题
已知：在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F，OE、OF的延长线交大圆于AB。
求证：AC＝DB
。O
C
A
E
B
D
F
M
3
4
1
2

3、思考题
已知：在以O点为圆心的两个同心圆中。大圆的弦CD交小圆于E、F，OE、OF的延长线交大圆于AB。
求证：AC＝DB
。O
C
A
E
B
D
F