冀教版九年级数学下册第三十二章投影与视图达标测试卷（word版含答案）
文档属性
| 名称 | 冀教版九年级数学下册第三十二章投影与视图达标测试卷（word版含答案） |
|
|
| 格式 | doc | ||
| 文件大小 | 206.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 00:00:00 | ||
文档简介
第三十二章达标测试卷
一、选择题(1～10题每题3分，11～16题每题2分，共42分)
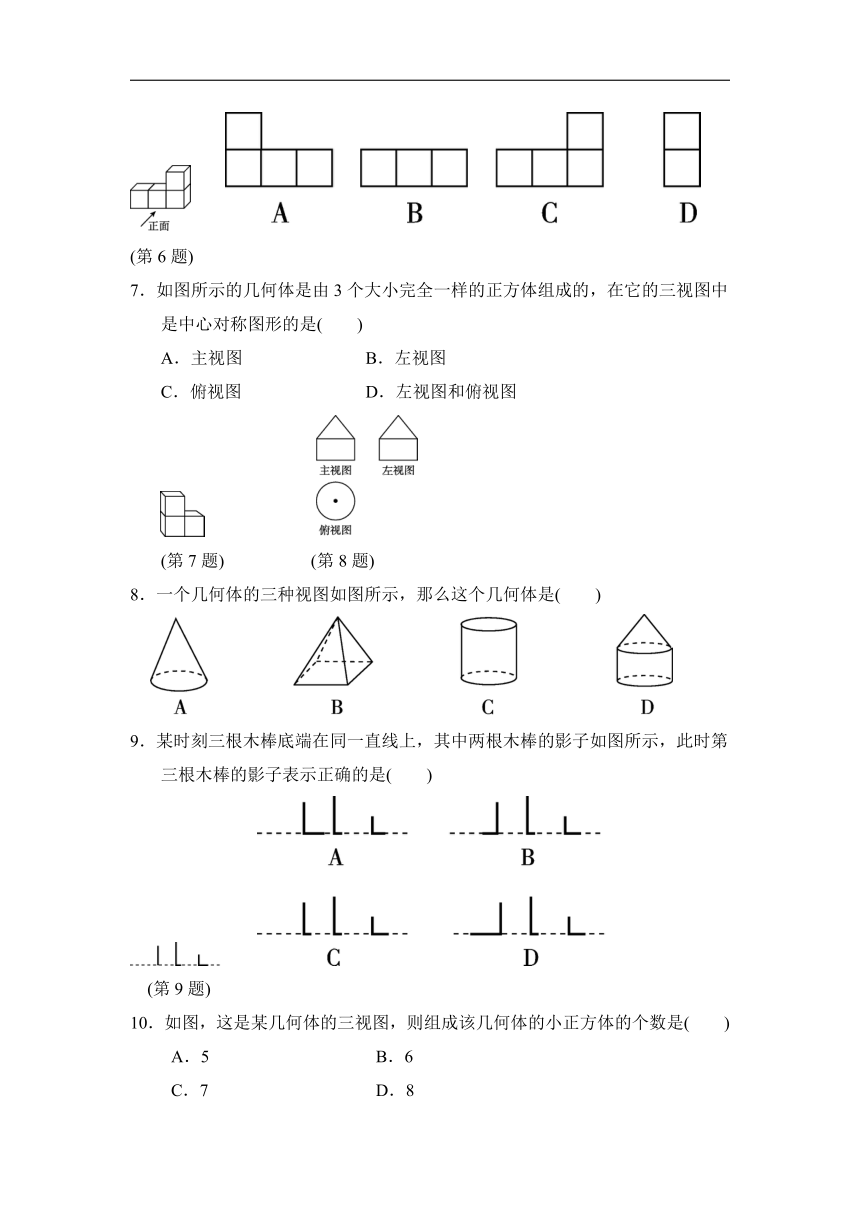
1．下列几何体中，主视图和左视图都为矩形的是( )
2．如图，这是一个长方体包装盒，则它的表面展开图可能是( )
(第2题) (第3题)
3．如图所示的几何体的俯视图是( )
4．把一个六棱柱按如图的方式摆放，光线由上向下照射此六棱柱时的正投影是( )
(第4题)
5．在一个晴朗的上午，小明将一块正方形木板放在阳光下，正方形木板在地面上形成的投影不可能是( )
6．如图所示的几何体的左视图是( )
(第6题)
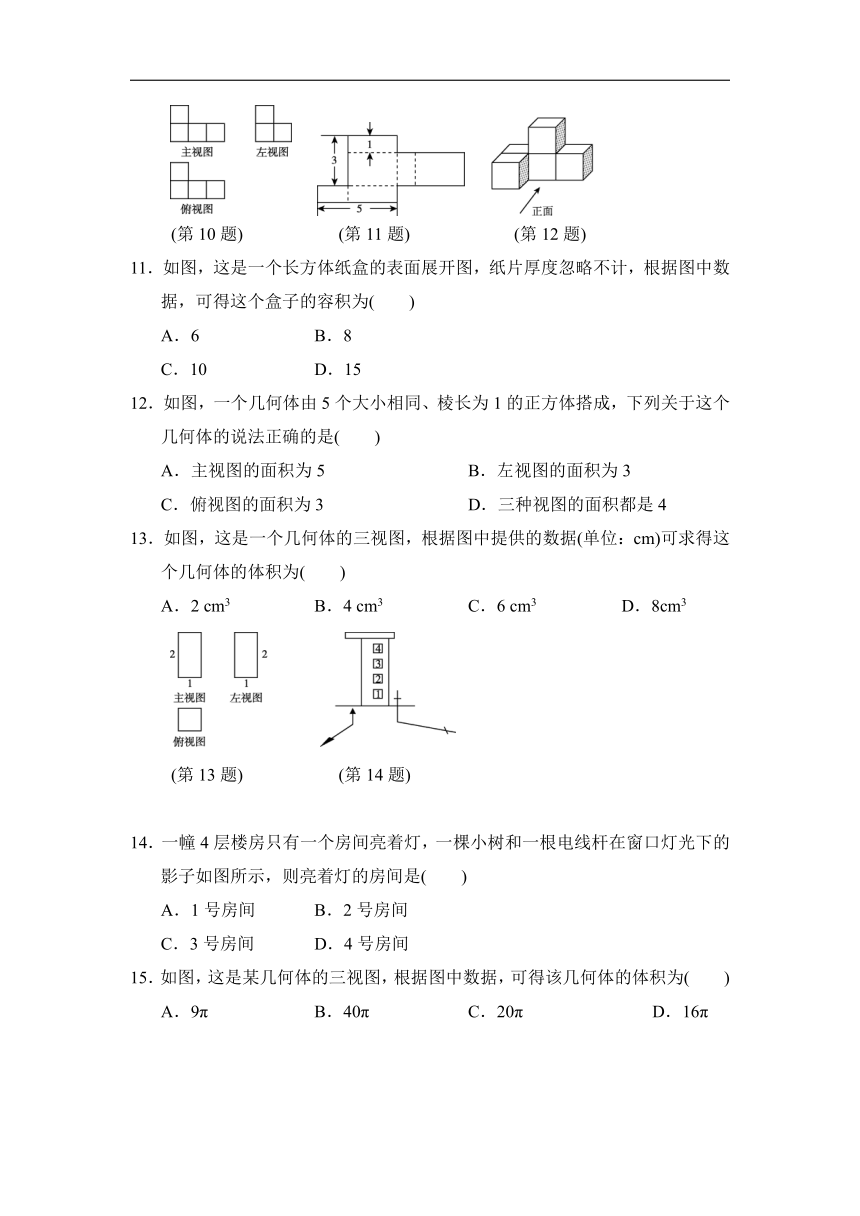
7．如图所示的几何体是由3个大小完全一样的正方体组成的，在它的...
一、选择题(1～10题每题3分，11～16题每题2分，共42分)
1．下列几何体中，主视图和左视图都为矩形的是( )
2．如图，这是一个长方体包装盒，则它的表面展开图可能是( )
(第2题) (第3题)
3．如图所示的几何体的俯视图是( )
4．把一个六棱柱按如图的方式摆放，光线由上向下照射此六棱柱时的正投影是( )
(第4题)
5．在一个晴朗的上午，小明将一块正方形木板放在阳光下，正方形木板在地面上形成的投影不可能是( )
6．如图所示的几何体的左视图是( )
(第6题)
7．如图所示的几何体是由3个大小完全一样的正方体组成的，在它的...
常见问题
这份试卷适用于什么教材版本？
本试卷适用于冀教版相关教学场景，可在21世纪教育网检索同版本配套资源。
适用学段和科目是什么？
适用学段与科目：初中、0、数学。
文件是什么格式，大小多少？
文件格式为 DOC，文件大小约 206.9KB。
文档主要包含哪些内容？
第三十二章达标测试卷一、选择题(1～10题每题3分，11～16题每题2分，共42分)1．下列几何体中，主视图和左视图都为矩形的是( )2．如图，这是一个长方体包装盒，则它的表面展开图可能是( ) (第2题) (第3题)3．如…
如何获取完整文档？
页面提供 5 页预览图片，完整文档可通过21世纪教育网下载页 /t/8218994 获取。