人教版六年级上册数学同步教学课件-圆的面积(第4课时)(47张ppt)
文档属性
| 名称 | 人教版六年级上册数学同步教学课件-圆的面积(第4课时)(47张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 18.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 09:39:56 | ||
图片预览





文档简介
圆的面积(第4课时)
文文
果果
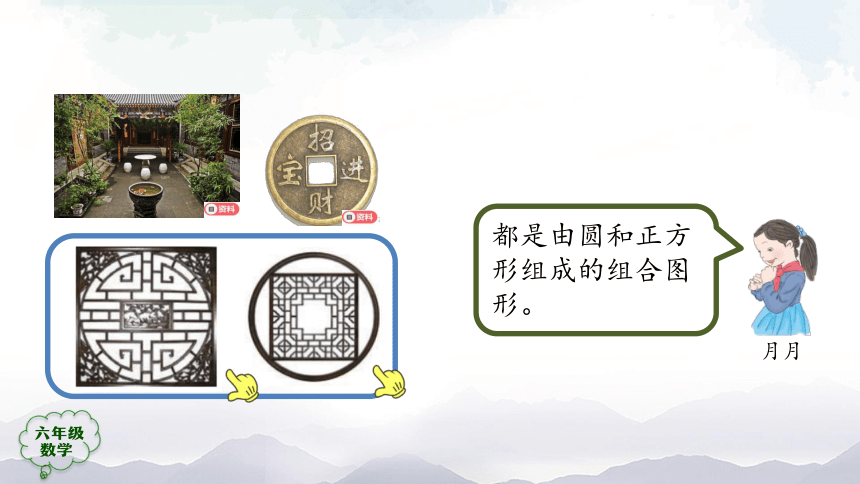
都是由圆和正方形组成的组合图形。
月月
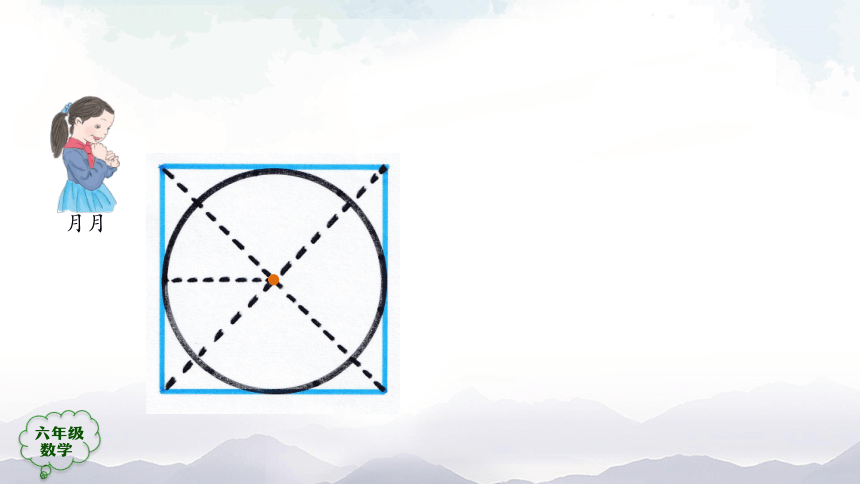
你能尝试着在正方形内画一个最大的圆吗?
老师
月月
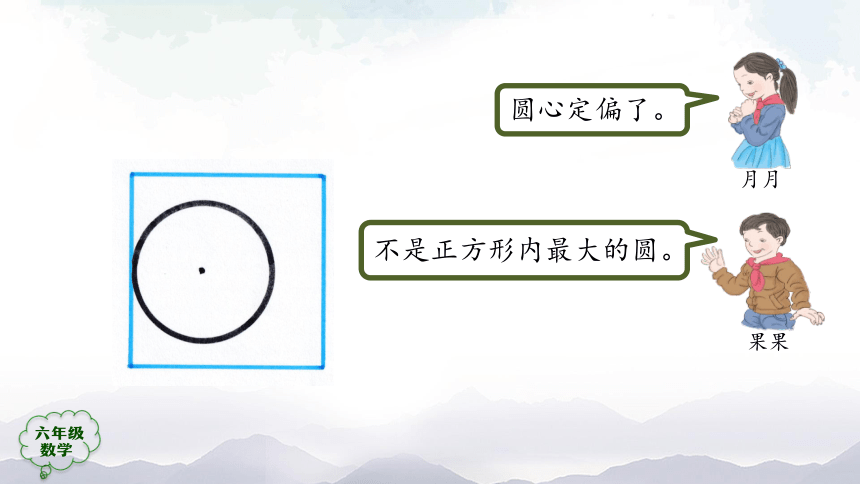
圆心定偏了。
果果
不是正方形内最大的圆。
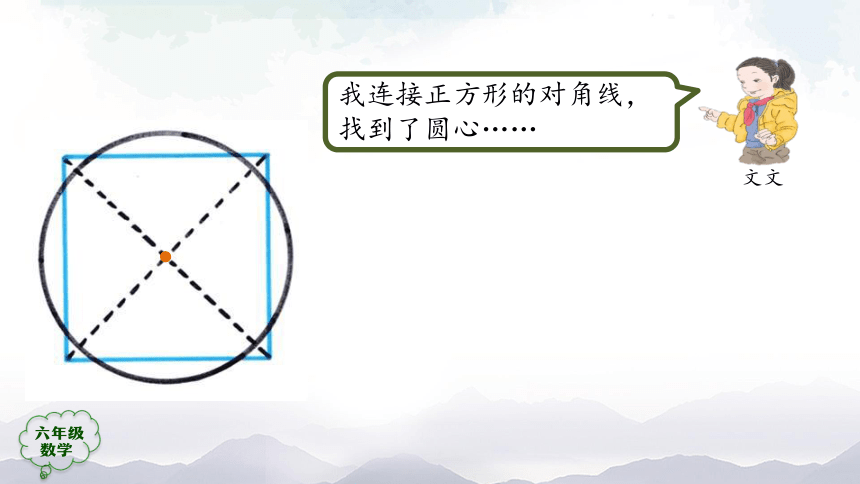
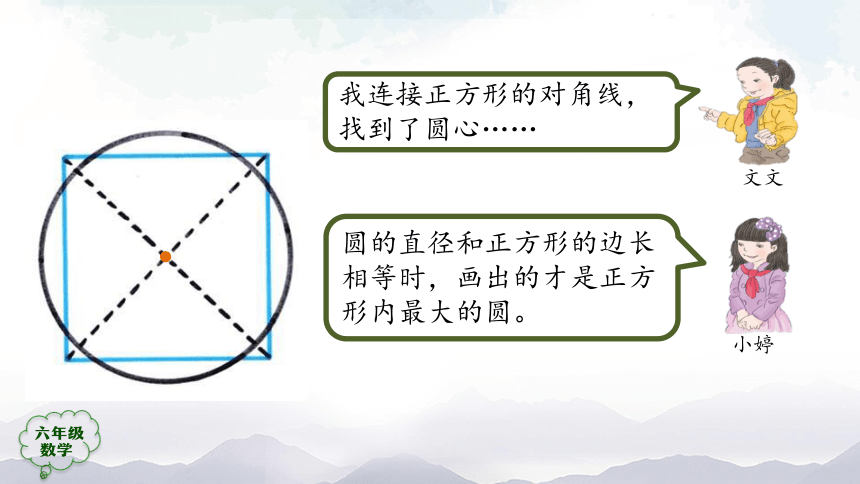
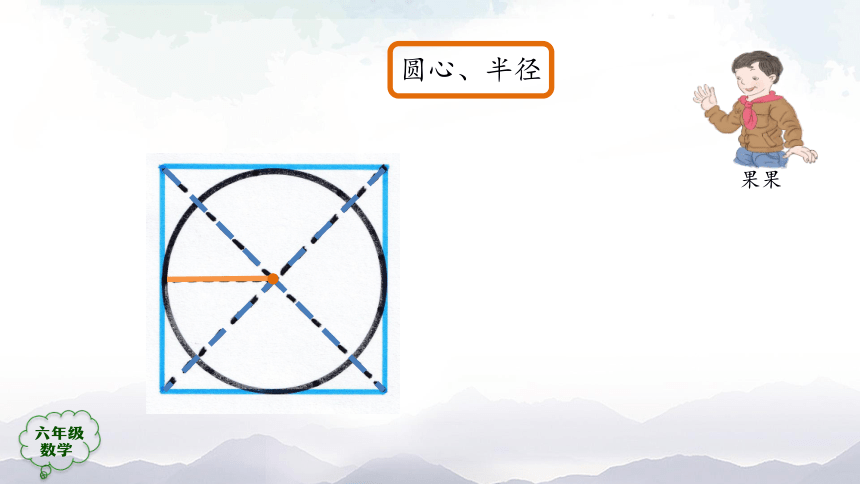
我连接正方形的对角线,找到了圆心……
文文
我连接正方形的对角线,找到了圆心……
文文
圆的直径和正方形的边长相等时,画出的才是正方形内最大的圆。
小婷
月月
圆心、半径
果果
月月
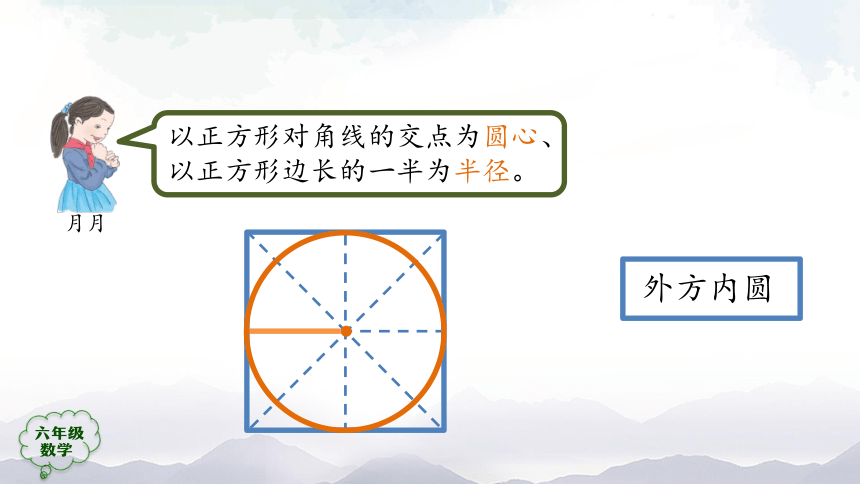
以正方形对角线的交点为圆心、以正方形边长的一半为半径。
外方内圆
如果让正方形的四个顶点都在圆上,使它成为圆内最大的正方形,这个圆又该怎样画呢?
老师
正方形对角线的交点是圆心。正方形对角线的一半是半径。
外圆内方
乐乐
它们有什么联系呢?
老师
果果
正方形的大小与位置都不同。
我觉得这两幅图中圆的大小相同。
月月
果果
正方形的大小与位置都不同。
求圆和正方形之间部分的面积。
乐乐
求圆或者正方形的面积。
果果
阅读与理解
要求圆的面积……
要求正方形的面积……
文文
阅读与理解
用较大的面积减去较小的面积。
阅读与理解
小婷
要求圆的面积……
要求正方形的面积……
文文
图中两个圆的半径都是1 m ,
求出正方形和圆之间的面积。
r=1 m
r=1m
分析与解答
r=1 m
分析与解答
S圆=πr?
分析与解答
乐乐
r=1 m
正方形的边长=圆的直径
分析与解答
小婷
r=1 m
正方形的对角线=圆的直径
乐乐
分析与解答
r=1 m
果果
三角形的底是圆的直径,
高是圆的半径。
r=1 m
分析与解答
不仅发现了图形的特点,还借助了三角形的面积计算方法求出了中间部分的面积。
文文
分析与解答
r=1 m
小三角形的底和高是圆的半径。
文文
分析与解答
r=1 m
r
r
如果两个圆的半径都是r,结果又是怎样的?
回顾与反思
月月
r
文文
回顾与反思
乐乐
正方形等分成2个三角形。
回顾与反思
r
正方形等分成4个小三角形。
回顾与反思
小婷
r
(2 r)?-3.14×r?=0.86 r?
3.14×r?-2 r?=1.14 r?
月月
回顾与反思
3.14×r?-2 r?=1.14 r?
(2 r)?-3.14×r?=0.86 r?
老师
回顾与反思
两个正方形之间的面积是2 r?。
S大正方形=4 r?
r
S圆 =πr?
S小正方形=2 r?
大正方形面积∶圆的面积∶小正方形的面积=4∶π∶2
大正方形面积是小正方形面积的2倍。
右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。外面的圆与内部的正方形之间的面积是多少?
借助三角形的面积,计算正方形的面积,再算面积差。
d=24 cm
小婷
我利用刚刚发现的规律……
d=24 cm
文文
乐乐
认识了两个新的组合图形……
乐乐
认识了两个新的组合图形……
果果
我还知道了……
阅读与理解
分析与解答
回顾与反思
文文
阅读与理解
分析与解答
回顾与反思
我觉得转化思想特别有用!
月月
文文
乐乐
认识了两个新的组合图形……
阅读与理解
分析与解答
回顾与反思
我觉得转化思想特别有用!
月月
(2 r)?-3.14×r?=0.86 r?
3.14×r?-2 r?=1.14 r?
一般
特殊
r =1 m
大正方形面积∶圆面积∶小正方形面积
4 ∶ π ∶ 2
学
习
内
容
数学书第69、70页。
课
后
练
习
完成数学书第72页第9题、第74页第15题。
文文
果果
都是由圆和正方形组成的组合图形。
月月
你能尝试着在正方形内画一个最大的圆吗?
老师
月月
圆心定偏了。
果果
不是正方形内最大的圆。
我连接正方形的对角线,找到了圆心……
文文
我连接正方形的对角线,找到了圆心……
文文
圆的直径和正方形的边长相等时,画出的才是正方形内最大的圆。
小婷
月月
圆心、半径
果果
月月
以正方形对角线的交点为圆心、以正方形边长的一半为半径。
外方内圆
如果让正方形的四个顶点都在圆上,使它成为圆内最大的正方形,这个圆又该怎样画呢?
老师
正方形对角线的交点是圆心。正方形对角线的一半是半径。
外圆内方
乐乐
它们有什么联系呢?
老师
果果
正方形的大小与位置都不同。
我觉得这两幅图中圆的大小相同。
月月
果果
正方形的大小与位置都不同。
求圆和正方形之间部分的面积。
乐乐
求圆或者正方形的面积。
果果
阅读与理解
要求圆的面积……
要求正方形的面积……
文文
阅读与理解
用较大的面积减去较小的面积。
阅读与理解
小婷
要求圆的面积……
要求正方形的面积……
文文
图中两个圆的半径都是1 m ,
求出正方形和圆之间的面积。
r=1 m
r=1m
分析与解答
r=1 m
分析与解答
S圆=πr?
分析与解答
乐乐
r=1 m
正方形的边长=圆的直径
分析与解答
小婷
r=1 m
正方形的对角线=圆的直径
乐乐
分析与解答
r=1 m
果果
三角形的底是圆的直径,
高是圆的半径。
r=1 m
分析与解答
不仅发现了图形的特点,还借助了三角形的面积计算方法求出了中间部分的面积。
文文
分析与解答
r=1 m
小三角形的底和高是圆的半径。
文文
分析与解答
r=1 m
r
r
如果两个圆的半径都是r,结果又是怎样的?
回顾与反思
月月
r
文文
回顾与反思
乐乐
正方形等分成2个三角形。
回顾与反思
r
正方形等分成4个小三角形。
回顾与反思
小婷
r
(2 r)?-3.14×r?=0.86 r?
3.14×r?-2 r?=1.14 r?
月月
回顾与反思
3.14×r?-2 r?=1.14 r?
(2 r)?-3.14×r?=0.86 r?
老师
回顾与反思
两个正方形之间的面积是2 r?。
S大正方形=4 r?
r
S圆 =πr?
S小正方形=2 r?
大正方形面积∶圆的面积∶小正方形的面积=4∶π∶2
大正方形面积是小正方形面积的2倍。
右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。外面的圆与内部的正方形之间的面积是多少?
借助三角形的面积,计算正方形的面积,再算面积差。
d=24 cm
小婷
我利用刚刚发现的规律……
d=24 cm
文文
乐乐
认识了两个新的组合图形……
乐乐
认识了两个新的组合图形……
果果
我还知道了……
阅读与理解
分析与解答
回顾与反思
文文
阅读与理解
分析与解答
回顾与反思
我觉得转化思想特别有用!
月月
文文
乐乐
认识了两个新的组合图形……
阅读与理解
分析与解答
回顾与反思
我觉得转化思想特别有用!
月月
(2 r)?-3.14×r?=0.86 r?
3.14×r?-2 r?=1.14 r?
一般
特殊
r =1 m
大正方形面积∶圆面积∶小正方形面积
4 ∶ π ∶ 2
学
习
内
容
数学书第69、70页。
课
后
练
习
完成数学书第72页第9题、第74页第15题。
