4.2确定圆的条件课件

(共23张PPT)
一位考古学家在长沙马王堆汉墓挖掘时，发现一圆形瓷器碎片，你能帮助这位考古学家画出这个碎片所在的整圆，以便于进行深入的研究吗？
要确定一个圆必须满足几个条件
1、过一点可以作几条直线？
2、过几点可确定一条直线？
过几点可以确定一个圆呢？
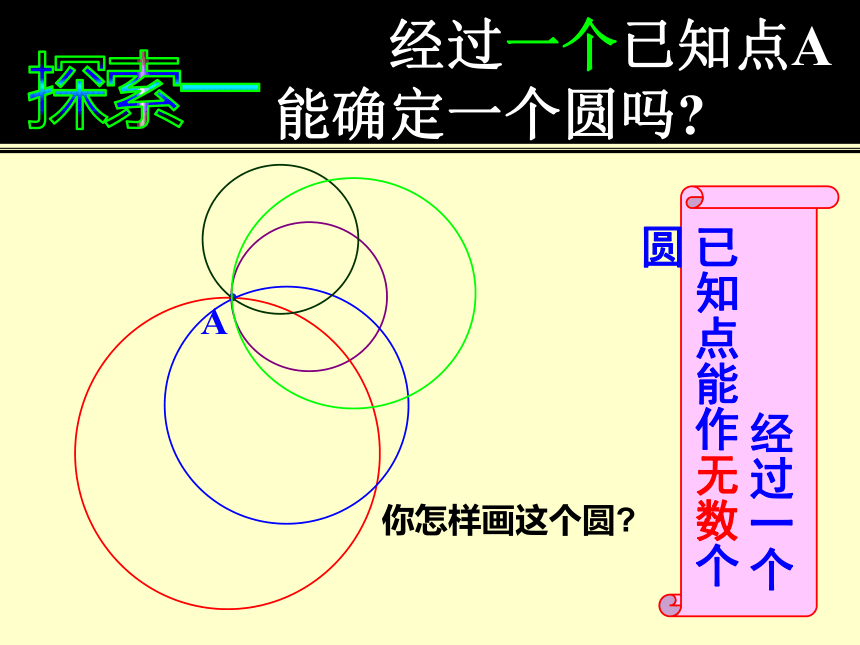
经过一个已知点A能确定一个圆吗
A
经过一个已知点能作无数个圆
你怎样画这个圆
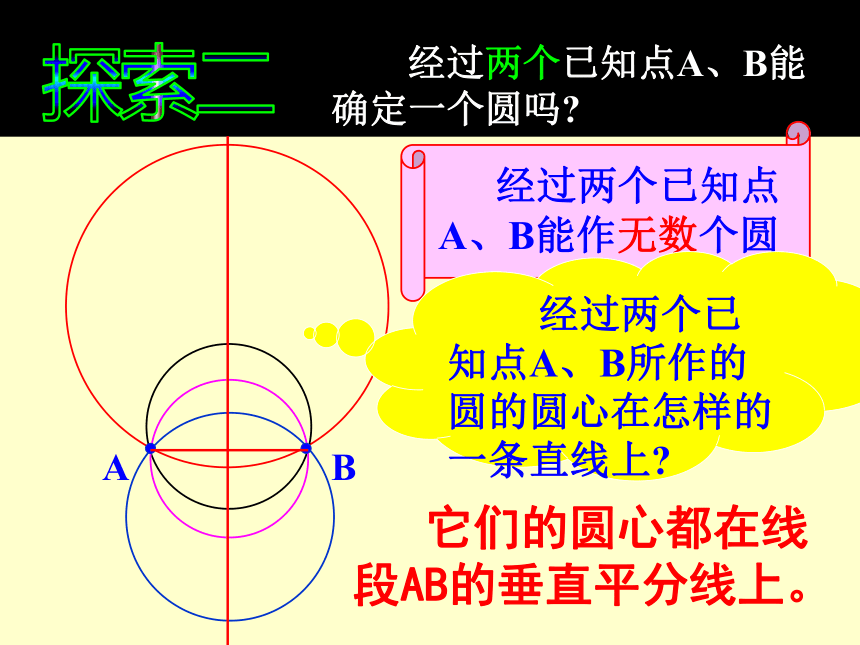
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的垂直平分线上。
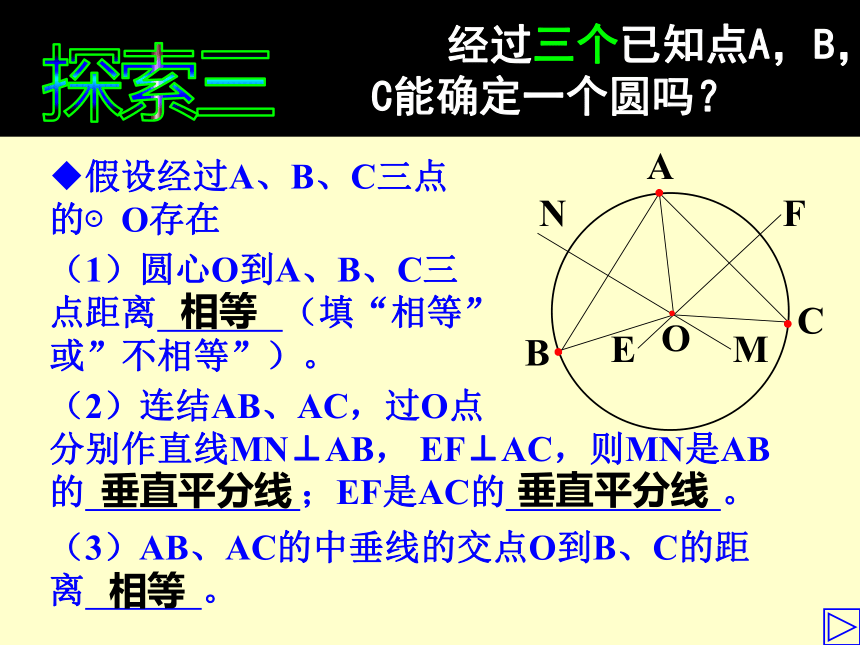
经过三个已知点A，B，C能确定一个圆吗？
假设经过A、B、C三点的⊙O存在
（1）圆心O到A、B、C三点距离 （填“相等”或”不相等”）。
（2）连结AB、AC，过O点 分别作直线MN⊥AB， EF⊥AC，则MN是AB的 ；EF是AC的 。
（3）AB、AC的中垂线的交点O到B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
A
B
C
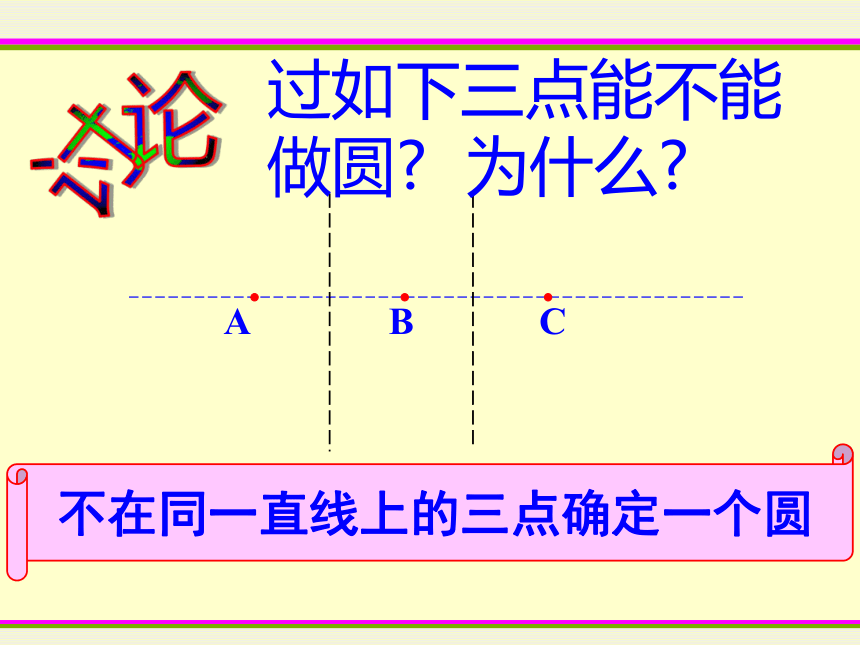
过如下三点能不能做圆 为什么
不在同一直线上的三点确定一个圆
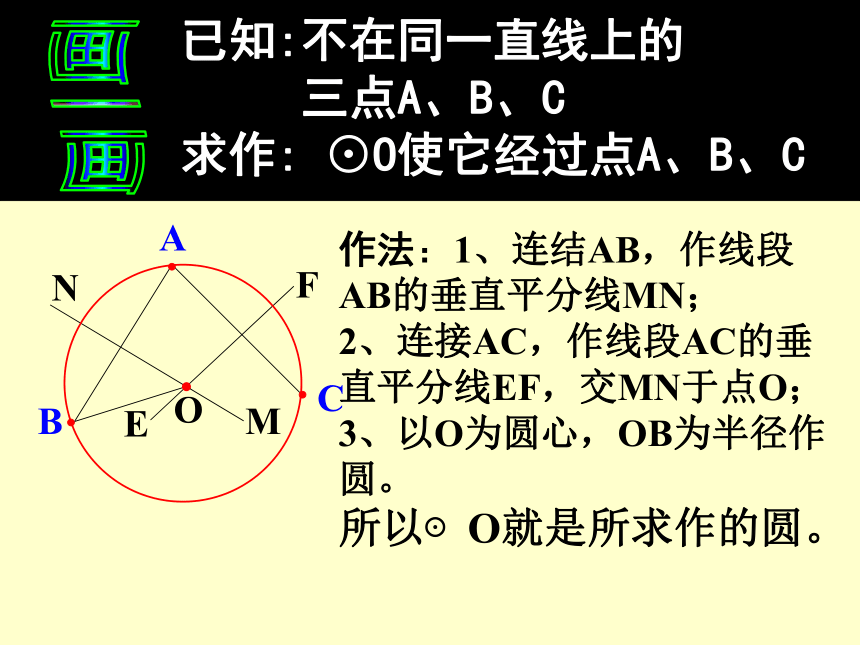
已知:不在同一直线上的
三点A、B、C
求作: ⊙O使它经过点A、B、C
作法：1、连结AB，作线段AB的垂直平分线MN；
2、连接AC，作线段AC的垂直平分线EF，交MN于点O；
3、以O为圆心，OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
现在你知道了怎样将一个如图所示的破损的圆盘复原了吗？
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心，OC长为半径作圆。
⊙O即为所求。
A
B
C
O
已知△ABC，用直尺和圆规作出过点A、B、C的圆
A
B
C
O
经过三角形各个顶点的圆 叫做三角形的外接圆，外接圆 的圆心叫做三角形的外心， 这个三角形叫做圆的内接三角形。
如图：⊙O是△ABC的外接圆， △ABC是⊙O的内接三角形，点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点，它到三角形的三个顶点的距离相等。
C
A
B
O
如图，请找出图中圆的圆心，并写出你找圆心的方法
A
B
C
O
画出以下三角形的外接圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、比较这三个三角形外心的位置，你有何发现？
（图一）
（图二）
（图三）
2、图二中，若AB=3，BC=4，则它的外接圆半径是多少？
某市要建一个圆形公园，要求公园刚好把动物园A，植物园B和人工湖C包括在内，又要使这个圆形的面积最小，请你给出这个公园的施工图。（A、B、C不在同一直线上）
植物园
动物园
人工湖
图中工具的CD边所在直线恰好垂直平分AB边，怎样用这个工具找出一个圆的圆心。
C
A
B
D
· 圆心
练一练
1.下列命题不正确的是
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能画圆.
2.三角形的外心具有的性质是
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
⊙
书P125 练习
判断：
1、经过三点一定可以作圆。（ ）
2、三角形的外心就是这个三角形两边垂直平分线的交点。（ ）
3、三角形的外心到三边的距离相等。（ ）
4、等腰三角形的外心一定在这个三角形内。（ ）
×
√
×
×
（1）只有确定了圆心和圆的半径，这个圆的位置和大小才唯一确定。
（2）经过一个已知点能作无数个圆！
（3）经过两个已知点A、B能作无数个圆！这些圆的圆心在线段AB的垂直平分线上。
（4）不在同一直线上的三个点确定一个圆。
（5）外接圆，外心的概念。
驶向胜利的彼岸
四边形与圆的位置关系
我们可以证明圆内接四边的两个重要性质:
●O
A
B
C
D
1.圆内接四边形对角互补.
2.圆内接四边形对的一个外角等于它的内对角.
C
O
D
B
A
如图：圆内接四边形ABCD中，
∵ ∠BAD度数=弧BCD度数的一半,∠BCD度数=弧BAD度数的一半.
弧BCD度数+弧BAD度=360°，
∴∠BAD＋∠BCD＝
180°.
同理∠ABC＋∠ADC＝180°.
圆内接四边形的对角互补.
四边形与圆的位置关系
驶向胜利的彼岸
如果延长BC到E，那么
∠DCE＋∠BCD ＝
180°.
∴∠A＝∠DCE.
又 ∵∠A ＋∠BCD＝ 180°，
C
O
D
B
A
E
驶向胜利的彼岸
四边形与圆的位置关系
因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.
圆内接四边形的一个外角等于它的内对角.