一元二次方程复习课件
图片预览











文档简介
(共48张PPT)
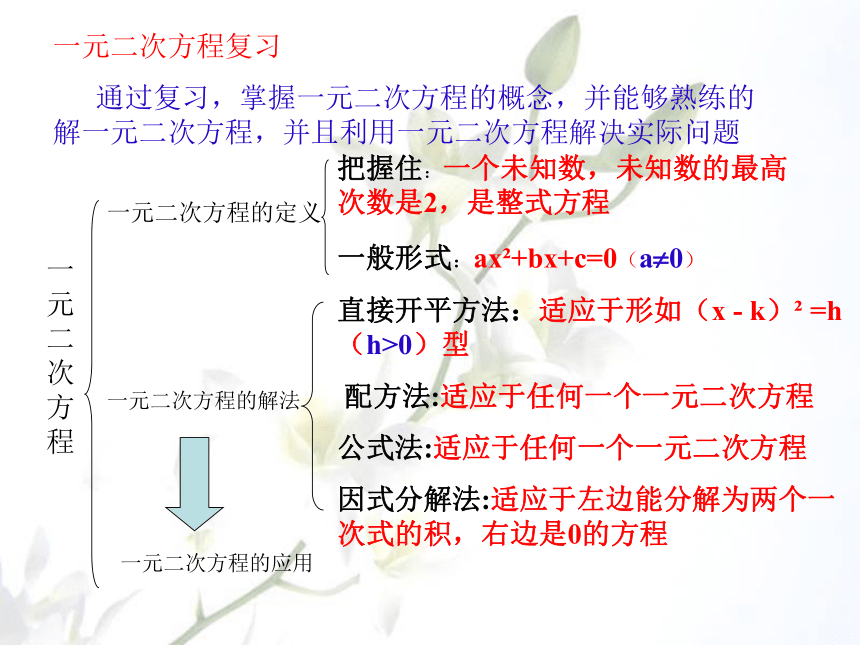
一元二次方程复习
一元二次方程复习
通过复习,掌握一元二次方程的概念,并能够熟练的解一元二次方程,并且利用一元二次方程解决实际问题
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
把握住:一个未知数,未知数的最高次数是2,是整式方程
一般形式:ax +bx+c=0(a 0)
直接开平方法:适应于形如(x - k) =h(h>0)型
配方法:适应于任何一个一元二次方程
公式法:适应于任何一个一元二次方程
因式分解法:适应于左边能分解为两个一次式的积,右边是0的方程
一、一元二次方程的概念
引例:判断下列方程是不是一元二次方程
(1)4x - x + 3 =0 (2)3x - y -1=0
(3)ax +bx+c=0 (4)x + =0
问题1、方程xy +y =2是一元二次方程吗?是关于x的一元二次方程吗?是关于y的一元二次方程吗?
注意:一元二次方程的三个要素及一个条件
2、已知关于x的方程(m -1)x +(m-1)x-2m+1=0,当m= 时是一元二次方程,当m= 时是一元一次方程,当m= 时,x=0。
3、若(m+2)x2 +(m-2)x-2=0是关于x的一元二次方程则m= 。
一元二次方程(关于x) 一般形式 二次项系数 一次项系数 常数项
3x -1=0
3x(x-2)=2(x-2)
1、
巩固提高:
二、一元二次方程的解法
你还记得吗?请你选择最恰当的方法解下列一元二次方程
1、3x -1=0 2、x(2x +3)=5(2x +3)
3、x -4x-20=0 4、2 x -5x+1=0
点评:1、形如(x-k) =h的方程可以用直接开平方法求解2、千万记住:方程的两边有相同的含有未知数的因式的时候不能两边都除以这个因式,因为这样能把方程的一个根丢失了。要利用因式分解法求解
3、当常数项很大时可以用配方法求解,
当我们不能利用上边的方法求解的时候就就可以用公式法求解,公式法是万能的。
跳跳,看看你能跳多高?
用配方法证明:关于x的方程(m -12m +37)x +3mx+1=0,无论m取何值,此方程都是一元二次方程
练习1、用最好的方法求解下列方程
1、(3x -2) - 49=0 2、(3x -4) =(4x -3)
3、 4y = 1 - y
解1、移项,得:(3x-2) =49
两边开平方,得:3x -2=±7
所以:x=
所以x1=3,x2=-
解2、
法一:两边开平方,得:3x-4=±(4x-3)
3x -4=4x-3或3x-4=-4x+3
-x=1或 7x=7
x=-1,x=1
法二、(3x-4) -(4x-3) =0
(3x-4+4x-3)(3x-4x+3)=0
(7x-7)(-x-1)=0
7x-7=0或-x-1=0
所以:x=1,x=-1
解3、方程整理为:
3y +8y -2=0
这里a=3,b=8,c=-2
b - 4ac=64 -4 3 (-2)=88
X=
检查你的复习效果:
1、用配方法解方程2x +4x +1 =0,配方后得到的方程是 。
2、一元二次方程ax +bx +c =0,若x=1是它的一个根,则a+b+c= ,若a -b+c=0,则方程必有一根为 。
3、
。
4、方程2 x -mx-m =0有一个根为 - 1,则m=
,另一个根为 。
2(x+1) =1
-1
5或-1
2或-1
2或1/2
0
1、阅读材料,解答问题
为了解方程(y -1) -3(y -1)+2=0,我们将y -1视为一个整体,设 ,则(y -1) =a ,原方程可以化为:(1)a - 3a+2=0,解得a1=1,a2=2。当a=1时,y -1=1,y =± ,当a=2时,y -1=2,y=±
所以原方程的解为:y1= ,y2 =- y 3=
y4= -
y -1=a
解答问题:1、在由原方程得到方程(1)的过程中,利用了
法达到了降次的目的,体现了 的数学思想。
2、用上述方法解下列方程:
一 快速抢答
1. 判断下列方程哪些是一元二次方程 并说明理由.
X
2
(4) z(3z-1)=3z2+1( )
(1) 2x=y2-1( )
(2) y2-2y-3=0( )
(3) x2---3=0( )
(4)y2=9( )
(5)y2-2y3+1=0( )
不是
是
不是
不是
是
不是
三个条件:(1)是整式方程. (2)只含有一个未知数. (3)未知数的最高次数是2
2.方程(m-2)xImI+3mx+1=0是关于X的一元二次方程,则m=( )
_2
3.关于X的方程(K2-1)X2+2(K-1)X+44=0 当K______时,为一元二次方程,当K=__ 时为一元一次方程.
≠±1
-1
4.一元二次方程的一般形式是_____ ________________.
ax2+bx+c=0 (a≠0)
5.方程(2X-1)(X+5)=6X的二次项系数是( )一次项系数是( )常数项是( )
2
3
-5
二. 做一做
1.选用适当的方法解下列方程: (1)2x2-5=0 (2)3x2=4x (3)4x2=0 (4)y2-10y-10=0 (5)16(x-1)2=9(2x+1)2
缺少一次项常用直接开平方法,缺少常数项常用因式分解法,当一边为零另一边易因式分解时也常用________________.公式法和配方法适用于任何一个一元二次方程(b2-4ac≥0)
因式分解法
一、一元二次方程的根的判断式
【例1】不解方程,判断下列方程实根的个数.
解 (1)
∴ 原方程有两个不相等的实数根.
∴ 原方程有两个相等的实数根.
(2) 原方程可化为:
例1
一、一元二次方程的根的判断式
【例1】不解方程,判断下列方程实根的个数.
方法提炼:△与0的大小关系决定方程实根的情况;另外,在求判断式时,务必先把方程变形为一元二次方程的一般形式.
解 (3)
∴ 原方程没有实数根.
原方程可化为:
例1
一、一元二次方程的根的判断式
【例2】解一元二次方程 .
解 法一(因式分解)
移项,得
①方程化为一般形式
解题步骤
②因式分解成A.B=0 的形式
③A=0或B=0
④写出方程的两个根
方程左边因式分解,得
例2解法一
两边同时除以3,得
配方,得
开平方,得
①二次项系数化1.
②配方,并写成(x+m)2 =k(k≥0) 的形式.
③开平方,写出方程的两个解.
一、一元二次方程的根的判断式
【例2】解一元二次方程 .
解 法二(配方法)
解题步骤
例2解法二
一、一元二次方程的根的判断式
【例2】解一元二次方程 .
解 法三(公式法)
解题步骤
移项,得
①将方程化成一般式,并确定出a,b,c的值.
②求出b2-4ac的值
(特别注意b2-4ac<0)
③代入求根公式.
④写出方程的两个根.
故
例2解法三
二、一元二次方程的根与系数的关系
一元二次方程 的两个根为:
说明:一元二次方程根与系数的关系由十六世纪的法国数学家韦达发现,所以通常把此定理称为韦达定理.
知识点二:韦达定理
韦达定理成立的前提是 .
方程 可化为:
二、一元二次方程的根与系数的关系
例3(1)(2)
二、一元二次方程的根与系数的关系
例3(3)(4)
二、一元二次方程的根与系数的关系
方法提炼:
利用根与系数的关系求值,要熟练掌握以下等式变形:
韦达定理体现了整体代换思想.
例3方法提炼
二、一元二次方程的根与系数的关系
例4解法一
二、一元二次方程的根与系数的关系
例4解法二
-3
-2
-1
0
1
2
3
-1
-2
-3
1
2
3
x
y
问题:
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
如果直接设每盆植x株,怎样表示问题中相关的量
解:设每盆花苗增加的株数为x株,则每盆花苗有______株,平均单株盈利为__________元.
相等关系:
平均单株盈利×株数=10元
由题意,得
(x+3)(3-0.5x)=10
解这个方程,得:x1=1, x2=2
(x+3)
(3-0.5x)
如果设每盆花苗增加的株数为x株呢?
思考:这个问题设什么为x 有几种设法
化简,整理,得 x2-3x+2=0
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
问题探究
[问题]一商店一月份的利润是2500元,三月份的利润达到3000元,这二个月的平均月增长的百分率是多少?
思考:若设这二个月的平均月增长的百分率是x,则二月份的利润是:_____________元;
三月份的利润为:___________元.
可列出方程:
2500(1+x)
1、增长率问题的有关公式 :
增长数=基数╳增长率
实际数=基数+增长数
原始量╳(1+增加的百分数)增长次数 =后来的量
原始量╳(1-减少的百分数)降低次数 =后来的量
2、解这类问题的方程,用直接开平方法做简便。
[问题]截止到2000年12月31日,我国的上网计算机总数为892万台;截止到2002年12月31日,我国的上网计算机总数以达2083万台.
(1)求2000年12月31日至2002年12月31日我国的上网计算机台数的年平均增长率(精确到0.1%).
思考:(1)若设年平均增长率为x,你能用x的代数式表示2002年的台数吗
(2)已知2002年的台数是多少
(3)据此,你能列出方程吗
892(1+x)2=2083
.
.
.
.
.
年份
上网计算 机总台数
(万台)
3200
2400
1600
800
0
2000年
1月1日
2000年
12月31日
2001年
12月31日
2002年
12月31日
2003年
12月31日
350
892
1254
2083
3089
[问题] (2)上网计算机总数2001年12月31日至2003年12月31日的年平均增长率与2000年12月31日至2002年12月31日的年平均增长率相比,哪段时间年平均增长率较大?
.
.
.
.
.
年份
上网计算 机总台数
(万台)
3200
2400
1600
800
0
2000年
1月1日
2000年
12月31日
2001年
12月31日
2002年
12月31日
2003年
12月31日
350
892
1254
2083
3089
(1)已知哪段时间的年平均增长率
(2)需要求哪个时间段的年平均增长率
想一想:
试一试(1):
1、某农场粮食产量是:2003年1200万千克,2004年为1452万千克。如果平均每年的增长率为x,则可得方程 ----------------------------------------( )
A. 1200(1+x) =1452 B. 1200(1+2x)=1452
C. 1200(1+x%)2=1452 D. 1200(1+x%)=1452
2、某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均月增长率为x,则由题意得方程为-------------------------( )
200(1+x)2=1000 B. 200+200×2×x=1000
C. 200+200×3×x=1000 D. 200+200(1+x)+ 200(1+x)2=1000
A
D
3、某商场二月份的销售额为100万元,三月份的销售额下降了20%,商场从四月份起改进经营措施,销售额稳步增长,五月份销售额达到135.2万元,求四、五两个月的平均增长率。
解:设四、五两个月的平均增长率为x,
根据题意,得:
整理得
某商厦今年一月份销售额为60万元,二月份由于某种原因,销售额下降了10%,以后改进管理,大大激发了全体员工的积极性,月销售额大幅上升,到四月份销售额猛增到96万元,求三、四月份平均每月增长的百分率是多少?(精确到0.1%)
解:设三、四月份平均每月增长率为x,依题意,得:
60(1-10%)(1+x)2=96
解得:
由于增长率不能为负数,故 不合题意,舍去。
所以 答(略)
暸望中考:
我国人口数量逐年增加,人均资源不足的矛盾日益突出。为实施可持续发展战略,我国把实行计划生育作为一项基本国策,如图是我国人口数量增长图,试根据图中的信息,回答下列问题:
(1)1950年到1990年我国人口增加了_______亿;2000年我国人口数量为_______亿。
(2)实行计划生育政策前,我国人口每5年增长10%,由于实行计划生育,我国从1990年到2000年这十年间就少出生了_____亿人。
(3)1990年到2000年这十年中,我国人口平均每5年的增长率是多少?
(参考数据:1.12=1.21 , 1.0872=1.182 )
5.6
13
0.31
X=0.087 ( x= -2.087<0 不合题意,舍去。)
拓展提高:
市场经济不仅使我们走上了富裕之路,而且让我们学会了科学的经营方法。个体户张某原计划按600元/套销售一批西装,但上市后销售不佳,为使资金正常运转,减少库存积压,张某将这批西装连续两次降价打折处理,调整价格到了384元/套,如果两次降价折扣相同,求每次降价率为多少?两次打折标示多少折?
解:设平均每次降价率为x,根据题意,得:
600(1-x)2=384.
解得 : 不合题意,舍去。
所以 ,即每次降价为20%.
第一次打折后价格为原价的1-x=80%,即打八折 。
第二次打折后价格为原价的(1-x)2=64%,即打六四折。答(略)
列出下列问题中关于未知数x的方程:
(1)、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程
x
x
x
3
X2+3x=4
合 作 交 流
合 作 交 流
(2)据国家统计局公布的数据,浙江省2001年全省实现生产总值6700亿元,2003年生产总值达9200亿元,求浙江省这两年实现 生产总值的平均增长率。
设年平均增长率为x,可列出方程
2500
5000
7500
10000
2001
2002
2003
年份
生产总值(亿元)
9200
7670
6700
6700(1+x)2=9200
1:判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5y ( ) ⑧3y2+4=5y ( )
1
x2
-
2
x
=0
√
√
√
×
×
×
√
×
趁 热 打 铁
下列方程中是一元二次方程的为( )
(A)、x2+3x=
(B)、2(X-1)+3x=2
(C)、x2=2+3x
(D)、x2+x3-4=0
2
x2
C
2:判断括号内未知数的值是不是方程的根:
代入法!
一般地,任何一个关于x的一元二次方程都 可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2 , bx , c分别为二次项、一次项和常数项,a,b分别称为二次项系数和一次项系数。
考
考
你
为什么 a≠0
1、当a=0,b≠0时,bx+c=0是一元一次方程。
b,c可以为零吗?
2、当a≠0 ,b=0时, 是一元二次方程。
3、当a≠0 ,c=0时, 是一元二次方程。
探究新知
例1:把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.
二次项系数
一次项系数
常数项
-5
9
4
3
1
4
-5
-3
0
2
5
练习1:填空
方程 一般式 二次项系数 一次项系数 常数项
2X2-x=4
√2y-4y2=0
(2x)2=(x+1)2
0.5x2=√5
2X2-x-4=0
2
-1
-4
0.5
0
0.5x2-√5 =0
-4y2 +√2y =0
-4
0
√2
3x2-2x-1=0
3
-2
-1
- √5
练习2:
把一元二次方程(x-√5 )(x+√5 )+(2x-1)2 =0
化为一般形式,正确的是( )
A、5x2-4x-4=0
B、x2-5=0
C、5x2-2x+1=0
D、5x2-4x+6=0
A
练习1:已知关于x的方程:(m- 4)x2+4x+6=0
1:当方程的一个根是3时,求m的值?
2:当m为何值时,方程是一元一次方程?
3:当m为何值时,方程是一元二次方程?
引伸拓展
(2)、秦新大世界有一种线衣从原来的每件40元,经两次调价后,调至每件32.4元,若两次调价的降价率均为x,则第一次调价后降至 元,第二次调价后降至 元。
可列方程为:
。
40(1-x)
40(1-x)2
40(1-x)2=32.4
某农场的产量两年内从50万kg增加到60.5万kg,问:平均每年增产百分之几?
分析:如果把每年的增长率看作是x(注意百分号已包含在x之中)则第一年的产量为50(1+x)万kg;而第二年是在第一年基础上增长的,增长率还是x,因此,第二年的产量为50(1+x)(1+x) ,即50(1+x)2万kg。
解:设平均每年的增长率为x,根据题意,得 50(1+x)2=60.5
∴(1+x)2=1.21
解之得x1=0.1=10%,
x2=-2.1(不合题意,舍去)
答:平均每年增产10%。
5. 商店里某种商品在两个月里降价两次,现在该商品每件的价格比两个月前下降了36%,问平均每月降价百分之几?
解:设平均每月降价的百分数为 ,
又设两个月前的价格为 元,则现在的价格为 元,
根据题意,得 ,
不合题意舍去.
.
答:平均每月降价 .
练习:
1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为 .
B
例1、 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,商场决定采取适当的降价措施。经 调查发现,在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件。如果商场通过销售这批衬衫每天要盈利1200元,衬衫的单价应降多少元?
每天的销售量 每件利润 总利润
降价前
降价后
如果设每件衬衫的单价降了x元.
20
40
20×40=800
40-x
20+2x
1200
分析:
相等关系:
销售总量×每件利润=总利润(降价后)
例2、 某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
每天的销售量 每件利润 总利润
提价前
提价后
如果将每件售价定为x元
200
200 - ×10
x -8
10-8=2
640
200×2=400
思考:如果设涨价了x元,如何列方程
分析
总销售量×每件利润 =总利润(提价后)
相等关系:
x -10
0.5
END
江苏省镇江第一中学欢迎您
一元二次方程复习
一元二次方程复习
通过复习,掌握一元二次方程的概念,并能够熟练的解一元二次方程,并且利用一元二次方程解决实际问题
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
把握住:一个未知数,未知数的最高次数是2,是整式方程
一般形式:ax +bx+c=0(a 0)
直接开平方法:适应于形如(x - k) =h(h>0)型
配方法:适应于任何一个一元二次方程
公式法:适应于任何一个一元二次方程
因式分解法:适应于左边能分解为两个一次式的积,右边是0的方程
一、一元二次方程的概念
引例:判断下列方程是不是一元二次方程
(1)4x - x + 3 =0 (2)3x - y -1=0
(3)ax +bx+c=0 (4)x + =0
问题1、方程xy +y =2是一元二次方程吗?是关于x的一元二次方程吗?是关于y的一元二次方程吗?
注意:一元二次方程的三个要素及一个条件
2、已知关于x的方程(m -1)x +(m-1)x-2m+1=0,当m= 时是一元二次方程,当m= 时是一元一次方程,当m= 时,x=0。
3、若(m+2)x2 +(m-2)x-2=0是关于x的一元二次方程则m= 。
一元二次方程(关于x) 一般形式 二次项系数 一次项系数 常数项
3x -1=0
3x(x-2)=2(x-2)
1、
巩固提高:
二、一元二次方程的解法
你还记得吗?请你选择最恰当的方法解下列一元二次方程
1、3x -1=0 2、x(2x +3)=5(2x +3)
3、x -4x-20=0 4、2 x -5x+1=0
点评:1、形如(x-k) =h的方程可以用直接开平方法求解2、千万记住:方程的两边有相同的含有未知数的因式的时候不能两边都除以这个因式,因为这样能把方程的一个根丢失了。要利用因式分解法求解
3、当常数项很大时可以用配方法求解,
当我们不能利用上边的方法求解的时候就就可以用公式法求解,公式法是万能的。
跳跳,看看你能跳多高?
用配方法证明:关于x的方程(m -12m +37)x +3mx+1=0,无论m取何值,此方程都是一元二次方程
练习1、用最好的方法求解下列方程
1、(3x -2) - 49=0 2、(3x -4) =(4x -3)
3、 4y = 1 - y
解1、移项,得:(3x-2) =49
两边开平方,得:3x -2=±7
所以:x=
所以x1=3,x2=-
解2、
法一:两边开平方,得:3x-4=±(4x-3)
3x -4=4x-3或3x-4=-4x+3
-x=1或 7x=7
x=-1,x=1
法二、(3x-4) -(4x-3) =0
(3x-4+4x-3)(3x-4x+3)=0
(7x-7)(-x-1)=0
7x-7=0或-x-1=0
所以:x=1,x=-1
解3、方程整理为:
3y +8y -2=0
这里a=3,b=8,c=-2
b - 4ac=64 -4 3 (-2)=88
X=
检查你的复习效果:
1、用配方法解方程2x +4x +1 =0,配方后得到的方程是 。
2、一元二次方程ax +bx +c =0,若x=1是它的一个根,则a+b+c= ,若a -b+c=0,则方程必有一根为 。
3、
。
4、方程2 x -mx-m =0有一个根为 - 1,则m=
,另一个根为 。
2(x+1) =1
-1
5或-1
2或-1
2或1/2
0
1、阅读材料,解答问题
为了解方程(y -1) -3(y -1)+2=0,我们将y -1视为一个整体,设 ,则(y -1) =a ,原方程可以化为:(1)a - 3a+2=0,解得a1=1,a2=2。当a=1时,y -1=1,y =± ,当a=2时,y -1=2,y=±
所以原方程的解为:y1= ,y2 =- y 3=
y4= -
y -1=a
解答问题:1、在由原方程得到方程(1)的过程中,利用了
法达到了降次的目的,体现了 的数学思想。
2、用上述方法解下列方程:
一 快速抢答
1. 判断下列方程哪些是一元二次方程 并说明理由.
X
2
(4) z(3z-1)=3z2+1( )
(1) 2x=y2-1( )
(2) y2-2y-3=0( )
(3) x2---3=0( )
(4)y2=9( )
(5)y2-2y3+1=0( )
不是
是
不是
不是
是
不是
三个条件:(1)是整式方程. (2)只含有一个未知数. (3)未知数的最高次数是2
2.方程(m-2)xImI+3mx+1=0是关于X的一元二次方程,则m=( )
_2
3.关于X的方程(K2-1)X2+2(K-1)X+44=0 当K______时,为一元二次方程,当K=__ 时为一元一次方程.
≠±1
-1
4.一元二次方程的一般形式是_____ ________________.
ax2+bx+c=0 (a≠0)
5.方程(2X-1)(X+5)=6X的二次项系数是( )一次项系数是( )常数项是( )
2
3
-5
二. 做一做
1.选用适当的方法解下列方程: (1)2x2-5=0 (2)3x2=4x (3)4x2=0 (4)y2-10y-10=0 (5)16(x-1)2=9(2x+1)2
缺少一次项常用直接开平方法,缺少常数项常用因式分解法,当一边为零另一边易因式分解时也常用________________.公式法和配方法适用于任何一个一元二次方程(b2-4ac≥0)
因式分解法
一、一元二次方程的根的判断式
【例1】不解方程,判断下列方程实根的个数.
解 (1)
∴ 原方程有两个不相等的实数根.
∴ 原方程有两个相等的实数根.
(2) 原方程可化为:
例1
一、一元二次方程的根的判断式
【例1】不解方程,判断下列方程实根的个数.
方法提炼:△与0的大小关系决定方程实根的情况;另外,在求判断式时,务必先把方程变形为一元二次方程的一般形式.
解 (3)
∴ 原方程没有实数根.
原方程可化为:
例1
一、一元二次方程的根的判断式
【例2】解一元二次方程 .
解 法一(因式分解)
移项,得
①方程化为一般形式
解题步骤
②因式分解成A.B=0 的形式
③A=0或B=0
④写出方程的两个根
方程左边因式分解,得
例2解法一
两边同时除以3,得
配方,得
开平方,得
①二次项系数化1.
②配方,并写成(x+m)2 =k(k≥0) 的形式.
③开平方,写出方程的两个解.
一、一元二次方程的根的判断式
【例2】解一元二次方程 .
解 法二(配方法)
解题步骤
例2解法二
一、一元二次方程的根的判断式
【例2】解一元二次方程 .
解 法三(公式法)
解题步骤
移项,得
①将方程化成一般式,并确定出a,b,c的值.
②求出b2-4ac的值
(特别注意b2-4ac<0)
③代入求根公式.
④写出方程的两个根.
故
例2解法三
二、一元二次方程的根与系数的关系
一元二次方程 的两个根为:
说明:一元二次方程根与系数的关系由十六世纪的法国数学家韦达发现,所以通常把此定理称为韦达定理.
知识点二:韦达定理
韦达定理成立的前提是 .
方程 可化为:
二、一元二次方程的根与系数的关系
例3(1)(2)
二、一元二次方程的根与系数的关系
例3(3)(4)
二、一元二次方程的根与系数的关系
方法提炼:
利用根与系数的关系求值,要熟练掌握以下等式变形:
韦达定理体现了整体代换思想.
例3方法提炼
二、一元二次方程的根与系数的关系
例4解法一
二、一元二次方程的根与系数的关系
例4解法二
-3
-2
-1
0
1
2
3
-1
-2
-3
1
2
3
x
y
问题:
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
如果直接设每盆植x株,怎样表示问题中相关的量
解:设每盆花苗增加的株数为x株,则每盆花苗有______株,平均单株盈利为__________元.
相等关系:
平均单株盈利×株数=10元
由题意,得
(x+3)(3-0.5x)=10
解这个方程,得:x1=1, x2=2
(x+3)
(3-0.5x)
如果设每盆花苗增加的株数为x株呢?
思考:这个问题设什么为x 有几种设法
化简,整理,得 x2-3x+2=0
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
问题探究
[问题]一商店一月份的利润是2500元,三月份的利润达到3000元,这二个月的平均月增长的百分率是多少?
思考:若设这二个月的平均月增长的百分率是x,则二月份的利润是:_____________元;
三月份的利润为:___________元.
可列出方程:
2500(1+x)
1、增长率问题的有关公式 :
增长数=基数╳增长率
实际数=基数+增长数
原始量╳(1+增加的百分数)增长次数 =后来的量
原始量╳(1-减少的百分数)降低次数 =后来的量
2、解这类问题的方程,用直接开平方法做简便。
[问题]截止到2000年12月31日,我国的上网计算机总数为892万台;截止到2002年12月31日,我国的上网计算机总数以达2083万台.
(1)求2000年12月31日至2002年12月31日我国的上网计算机台数的年平均增长率(精确到0.1%).
思考:(1)若设年平均增长率为x,你能用x的代数式表示2002年的台数吗
(2)已知2002年的台数是多少
(3)据此,你能列出方程吗
892(1+x)2=2083
.
.
.
.
.
年份
上网计算 机总台数
(万台)
3200
2400
1600
800
0
2000年
1月1日
2000年
12月31日
2001年
12月31日
2002年
12月31日
2003年
12月31日
350
892
1254
2083
3089
[问题] (2)上网计算机总数2001年12月31日至2003年12月31日的年平均增长率与2000年12月31日至2002年12月31日的年平均增长率相比,哪段时间年平均增长率较大?
.
.
.
.
.
年份
上网计算 机总台数
(万台)
3200
2400
1600
800
0
2000年
1月1日
2000年
12月31日
2001年
12月31日
2002年
12月31日
2003年
12月31日
350
892
1254
2083
3089
(1)已知哪段时间的年平均增长率
(2)需要求哪个时间段的年平均增长率
想一想:
试一试(1):
1、某农场粮食产量是:2003年1200万千克,2004年为1452万千克。如果平均每年的增长率为x,则可得方程 ----------------------------------------( )
A. 1200(1+x) =1452 B. 1200(1+2x)=1452
C. 1200(1+x%)2=1452 D. 1200(1+x%)=1452
2、某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均月增长率为x,则由题意得方程为-------------------------( )
200(1+x)2=1000 B. 200+200×2×x=1000
C. 200+200×3×x=1000 D. 200+200(1+x)+ 200(1+x)2=1000
A
D
3、某商场二月份的销售额为100万元,三月份的销售额下降了20%,商场从四月份起改进经营措施,销售额稳步增长,五月份销售额达到135.2万元,求四、五两个月的平均增长率。
解:设四、五两个月的平均增长率为x,
根据题意,得:
整理得
某商厦今年一月份销售额为60万元,二月份由于某种原因,销售额下降了10%,以后改进管理,大大激发了全体员工的积极性,月销售额大幅上升,到四月份销售额猛增到96万元,求三、四月份平均每月增长的百分率是多少?(精确到0.1%)
解:设三、四月份平均每月增长率为x,依题意,得:
60(1-10%)(1+x)2=96
解得:
由于增长率不能为负数,故 不合题意,舍去。
所以 答(略)
暸望中考:
我国人口数量逐年增加,人均资源不足的矛盾日益突出。为实施可持续发展战略,我国把实行计划生育作为一项基本国策,如图是我国人口数量增长图,试根据图中的信息,回答下列问题:
(1)1950年到1990年我国人口增加了_______亿;2000年我国人口数量为_______亿。
(2)实行计划生育政策前,我国人口每5年增长10%,由于实行计划生育,我国从1990年到2000年这十年间就少出生了_____亿人。
(3)1990年到2000年这十年中,我国人口平均每5年的增长率是多少?
(参考数据:1.12=1.21 , 1.0872=1.182 )
5.6
13
0.31
X=0.087 ( x= -2.087<0 不合题意,舍去。)
拓展提高:
市场经济不仅使我们走上了富裕之路,而且让我们学会了科学的经营方法。个体户张某原计划按600元/套销售一批西装,但上市后销售不佳,为使资金正常运转,减少库存积压,张某将这批西装连续两次降价打折处理,调整价格到了384元/套,如果两次降价折扣相同,求每次降价率为多少?两次打折标示多少折?
解:设平均每次降价率为x,根据题意,得:
600(1-x)2=384.
解得 : 不合题意,舍去。
所以 ,即每次降价为20%.
第一次打折后价格为原价的1-x=80%,即打八折 。
第二次打折后价格为原价的(1-x)2=64%,即打六四折。答(略)
列出下列问题中关于未知数x的方程:
(1)、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程
x
x
x
3
X2+3x=4
合 作 交 流
合 作 交 流
(2)据国家统计局公布的数据,浙江省2001年全省实现生产总值6700亿元,2003年生产总值达9200亿元,求浙江省这两年实现 生产总值的平均增长率。
设年平均增长率为x,可列出方程
2500
5000
7500
10000
2001
2002
2003
年份
生产总值(亿元)
9200
7670
6700
6700(1+x)2=9200
1:判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5y ( ) ⑧3y2+4=5y ( )
1
x2
-
2
x
=0
√
√
√
×
×
×
√
×
趁 热 打 铁
下列方程中是一元二次方程的为( )
(A)、x2+3x=
(B)、2(X-1)+3x=2
(C)、x2=2+3x
(D)、x2+x3-4=0
2
x2
C
2:判断括号内未知数的值是不是方程的根:
代入法!
一般地,任何一个关于x的一元二次方程都 可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2 , bx , c分别为二次项、一次项和常数项,a,b分别称为二次项系数和一次项系数。
考
考
你
为什么 a≠0
1、当a=0,b≠0时,bx+c=0是一元一次方程。
b,c可以为零吗?
2、当a≠0 ,b=0时, 是一元二次方程。
3、当a≠0 ,c=0时, 是一元二次方程。
探究新知
例1:把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.
二次项系数
一次项系数
常数项
-5
9
4
3
1
4
-5
-3
0
2
5
练习1:填空
方程 一般式 二次项系数 一次项系数 常数项
2X2-x=4
√2y-4y2=0
(2x)2=(x+1)2
0.5x2=√5
2X2-x-4=0
2
-1
-4
0.5
0
0.5x2-√5 =0
-4y2 +√2y =0
-4
0
√2
3x2-2x-1=0
3
-2
-1
- √5
练习2:
把一元二次方程(x-√5 )(x+√5 )+(2x-1)2 =0
化为一般形式,正确的是( )
A、5x2-4x-4=0
B、x2-5=0
C、5x2-2x+1=0
D、5x2-4x+6=0
A
练习1:已知关于x的方程:(m- 4)x2+4x+6=0
1:当方程的一个根是3时,求m的值?
2:当m为何值时,方程是一元一次方程?
3:当m为何值时,方程是一元二次方程?
引伸拓展
(2)、秦新大世界有一种线衣从原来的每件40元,经两次调价后,调至每件32.4元,若两次调价的降价率均为x,则第一次调价后降至 元,第二次调价后降至 元。
可列方程为:
。
40(1-x)
40(1-x)2
40(1-x)2=32.4
某农场的产量两年内从50万kg增加到60.5万kg,问:平均每年增产百分之几?
分析:如果把每年的增长率看作是x(注意百分号已包含在x之中)则第一年的产量为50(1+x)万kg;而第二年是在第一年基础上增长的,增长率还是x,因此,第二年的产量为50(1+x)(1+x) ,即50(1+x)2万kg。
解:设平均每年的增长率为x,根据题意,得 50(1+x)2=60.5
∴(1+x)2=1.21
解之得x1=0.1=10%,
x2=-2.1(不合题意,舍去)
答:平均每年增产10%。
5. 商店里某种商品在两个月里降价两次,现在该商品每件的价格比两个月前下降了36%,问平均每月降价百分之几?
解:设平均每月降价的百分数为 ,
又设两个月前的价格为 元,则现在的价格为 元,
根据题意,得 ,
不合题意舍去.
.
答:平均每月降价 .
练习:
1.某厂今年一月的总产量为500吨,三月的总产量为720吨,平均每月增长率是x,列方程( )
A.500(1+2x)=720 B.500(1+x)2=720 C.500(1+x2)=720 D.720(1+x)2=500
2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程
为 .
B
例1、 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,商场决定采取适当的降价措施。经 调查发现,在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件。如果商场通过销售这批衬衫每天要盈利1200元,衬衫的单价应降多少元?
每天的销售量 每件利润 总利润
降价前
降价后
如果设每件衬衫的单价降了x元.
20
40
20×40=800
40-x
20+2x
1200
分析:
相等关系:
销售总量×每件利润=总利润(降价后)
例2、 某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
每天的销售量 每件利润 总利润
提价前
提价后
如果将每件售价定为x元
200
200 - ×10
x -8
10-8=2
640
200×2=400
思考:如果设涨价了x元,如何列方程
分析
总销售量×每件利润 =总利润(提价后)
相等关系:
x -10
0.5
END
江苏省镇江第一中学欢迎您
