苏科版七年级数学上册 第三章 代数式 单元检测试题(Word版 有答案)
文档属性
| 名称 | 苏科版七年级数学上册 第三章 代数式 单元检测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 45.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 21:56:26 | ||
图片预览




文档简介
1049020010693400123190000第三章 代数式 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列各式中是代数式的是( )
A.a2-b2=0 B.4>3 C.a D.5x-2≠0
?
2. 下列说法正确的有( )个
①-25πxy2的系数为-25;②1是单项式;③2x-5是多项式;④单项式(-2)2x2y3的次数为7.
A.3 B.4 C.2 D.1
?
3. 用代数式表示“a、b两数的平方和减去它们乘积的2倍”,正确的是( )
A.a2+b2-2ab B.(a+b)2-2ab C.a2b2-2ab D.2(a2+b2-ab)
?
4. 下面的说法正确的是( )
A.单项式2πa2b的次数是4次 B.多项式a2b+bc+3的次数是2
C.3ab5的系数是3 D.x+1x+4不是多项式
?5. 在式子2ab,mn2+2m3,x,y+zx,0,5π,-2πpq3中单项式有( )
A.6个 B.5个 C.4个 D.3个
?
6. 下列式子中:12,3ab,m+2n,2x+3=1,st,整式的个数为( )
A.2个 B.3个 C.4个 D.5个
?
7. 下列式子中:13,1x+2,x3-y,π(x2-y2),16a2,7x-1,y2+8x,9a2+1a-2,单项式和多项式的个数分别为( )
A.2个,5个 B.2个,4个 C.3个,4个 D.2个,6个
?
8. 下列运算中,正确的是( )
A.3a+2b=5ab B.2a3+3a2=5a5 C.5a2-4a2=1 D.3a2b-3ba2=0
?
9. 下列说法正确的是( )
A.-33a2bc2的系数为-3,次数为27
B.xπ+y2+z23不是单项式,但是整式
C.1x+1是多项式
D.mx2+1一定是关于x的二次二项式
?
10. 如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第8层中含有正三角形个数是( )
A.54个 B.90个 C.102个 D.114个
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 如果a-b-2=0,那么代数式1-2a+2b的值是________.
?
12. 化简:3+[3a-2(a-1)]=________.
?
13. 若3xm-2yn+3与-5x5y2是同类项,则m+n=________.
?
14. 观察下列各式1×3=3=22-1,3×5=15=42-1,5×7=35=62-1,11×13=143=122-1…把你猜想到的规律用只含一个字母的等式表示出来________.
?15. 某班有女生a人,男生比女生的2倍少5人,则男生有________人.
?
16. 若x2-2x-2的值为0,则3x2-6x的值是________.
?
17. 若单项式12x2ym与-2xny3是同类项,则m=________,n=________.
?
18. 代数式-πa2b22的系数是________,次数是________.
?
19. 已知5x3ym与6xny2可以合并为一项,则mn的值是________.
?
20. 多项式12x|m|-(m+2)x+7是关于x的二次三项式,则m=________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 化简或求值:
①4x-(-3y+52x);?????????????????②5(3a2b-ab2)-4(-ab2+3a2b);
③(9a2-1.5ab+5b2)-(7a2-13ab+7b2),其中a=-12,b=1.
?
22. 关于x,y的多项式6mx2+4nxy+2x+2xy-x2+y+4不含二次项,求多项式2m2n+10m-4n+2-2m2n-4m+2n的值.
?
23. 把下列各式填在相应的大括号里:
x-7,13x,4ab,23a,5-3x,y,st,x+13,x7+y7,x2+x2+1,m-1m+1,8a3x,-1
单项式集合{?...};
多项式集合{?...};
整式集合{?...}.
?
24. 自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天生产5000个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋x个.
成本(元/个)
售价(元/个)
A
2
2.3
B
3
3.5
(1)用含x的式子表示每天的生产成本和每天获得的利润;
(2)当x=2000时,求每天的生产成本和每天获得的利润.
?
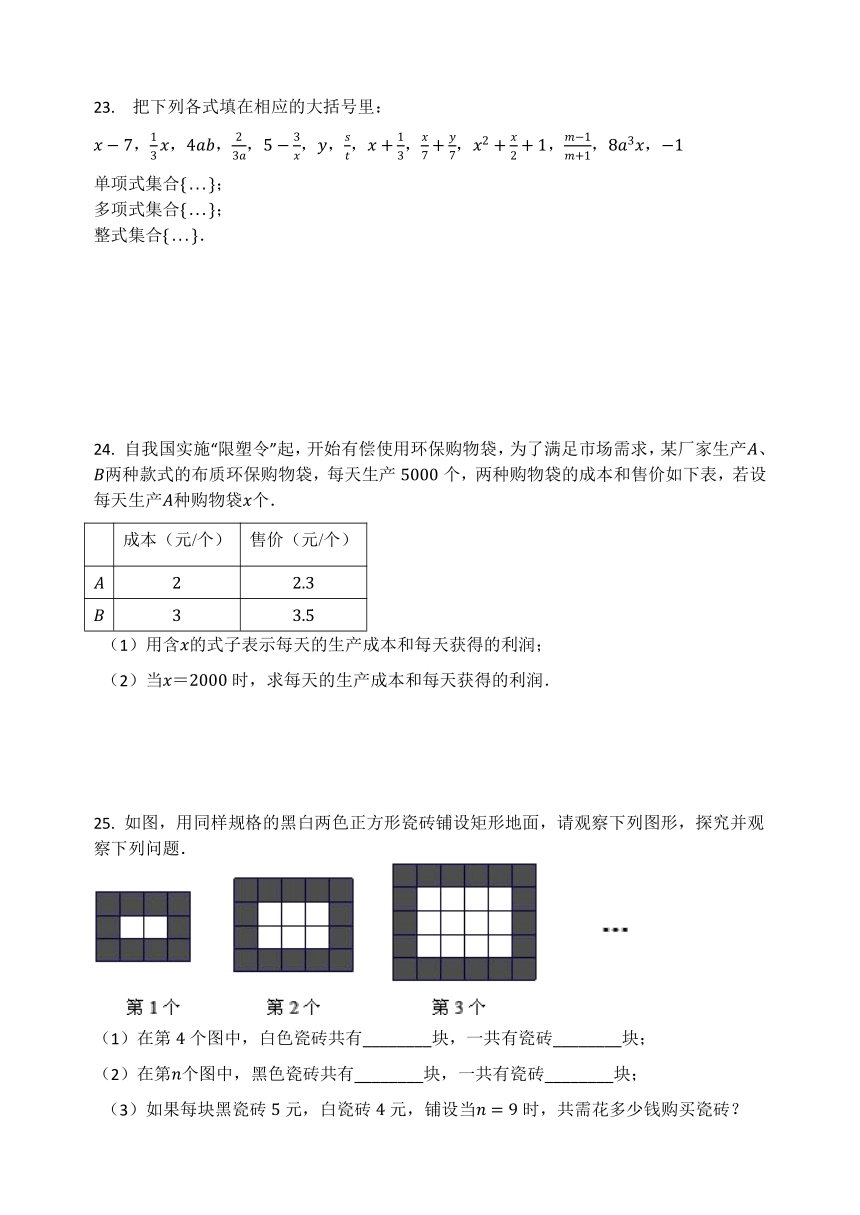
25. 如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题.
(1)在第4个图中,白色瓷砖共有________块,一共有瓷砖________块;
(2)在第n个图中,黑色瓷砖共有________块,一共有瓷砖________块;
(3)如果每块黑瓷砖5元,白瓷砖4元,铺设当n=9时,共需花多少钱购买瓷砖?
?26. 李师傅下岗后,做起来小生意,第一次进货,他以每件a元的价格购进了30件甲种小商品,以每件b元的价格购进了40件乙种小商品,且a(1)若李师傅将甲种商品提价40%,乙种商品提价30%全部出售,他获利多少元?(用含有a,b的式子表示结果)
(2)若李师傅将两种商品都以a+b2元的价格全部出售,他这次买卖是赚钱还是亏本,请说明理由?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:A:a2-b2=0为等式,不为代数式,故本项错误.
B:4>3为不等式,故本项错误.
C;a为代数式,故本项正确.
D:5x-2≠0为不等式,故本项错误.
故选:C.
2.
【答案】
D
【解答】
解:①-25πxy2的系数为-25π,故①错误;
②1是单项式,故②正确;
③2x不是单项式,所以2x-5不是多项式,故③错误;
④单项式(-2)2x2y3的次数为5,故④错误;
故选(D)
3.
【答案】
A
【解答】
解:a、b两数的平方和是a2+b2,
它们乘积的2倍是2ab,
则a、b两数的平方和减去它们乘积的2倍是:a2+b2-2ab;
故选A.
4.
【答案】
D
【解答】
解:A、单项式2πa2b的次数是3次,故选项错误;
B、多项式a2b+bc+3的次数是3,故选项错误;
C、3ab5的系数是35,故选项错误;
D、x+1x+4不是多项式是正确的.
故选D.
5.
【答案】
B
【解答】
解:2ab是单项式;
mn2+2m3含有加减运算是多项式;
x单独一个字母是一个单项式;
y+zx分母含有字母既不是单项式,也不是多项式;
0、5π都数字是一个单项式;
-2πpq3是单项式.
共有5个单项式.
故选:B.
6.
【答案】
B
【解答】
解:由整式的概念可得,12,3ab,m+2n是整式,
2x+3=1是等式不是整式,
st是分式不是整式.
故选B.
7.
【答案】
B
【解答】
解:所给式子中单项式有13,16a2一共2个;
多项式有:1x+2,x3-y,π(x2-y2),7x-1,y2+8x,一共4个.
故选B.
8.
【答案】
D
【解答】
解:A、不是同类项不能合并,故A错误;
B、合并同类项系数相加字母及指数不变,故B错误;
C、合并同类项系数相加字母及指数不变,故C错误;
D、合并同类项系数相加字母及指数不变,故D正确;
故选:D.
9.
【答案】
B
【解答】
解:A、-33a2bc2的系数为-33,次数为2+1+2=5,所以此选项不正确;
B、xπ+y2+z23不是单项式,是多项式,是整式,所以此选项正确;
C、1x+1不是多项式,是分式,所以此选项不正确;
D、因为m不确定,当m=0时,mx2+1=1,是单项式,当m≠0时,一定是关于x的二次二项式,所以此选项不正确.
故选B.
10.
【答案】
B
【解答】
根据题意分析可得:从里向外的第1层包括6个正三角形.第2层包括18个正三角形.此后,每层都比前一层多12个.依此递推,第8层中含有正三角形个数是6+12×7=90个.
故选:B.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
-3
【解答】
∵ a-b-2=0,
∴ a-b=2,
则原式=1-2(a-b)
=1-2×2
=1-4
=-3,
12.
【答案】
a+5
【解答】
解:原式=3+3a-2a+2=a+5,
故答案为:a+5
13.
【答案】
6
【解答】
解:∵ 3xm-2yn+3与-5x5y2是同类项,
∴ m-2=5n+3=2,
解得:m=7n=-1,
则m+n=7+(-1)=6.
故答案为:6.
14.
【答案】
(n-1)(n+1)=n2-1
【解答】
解:∵ 1×3=3=22-1,3×5=15=42-1,5×7=35=62-1,11×13=143=122-1…,
∴ 规律为:(n-1)(n+1)=n2-1.
故答案为:(n-1)(n+1)=n2-1.
15.
【答案】
(2a-5)
【解答】
解:依题意得:(2a-5).
16.
【答案】
6
【解答】
解:由x2-2x-2=0,
得到x2-2x=2,
则原式=3(x2-2x)=6.
故答案为:6.
17.
【答案】
3,2
【解答】
解:∵ 单项式12x2ym与-2xny3是同类项,
∴ n=2,m=3,
故答案为:3、2.
18.
【答案】
-12π,4
【解答】
解:代数式-πa2b22的系数是-12π,次数是4.
故答案为:-12π,4.
19.
【答案】
【解答】
此题暂无解答
20.
【答案】
2
【解答】
∵ 多项式是关于x的二次三项式,
∴ |m|=2,
∴ m=±2,
但-(m+2)≠0,
即m≠-2,
综上所述,m=2,故填空答案:2.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:①原式=4x+3y-52x=32x+3y;
②原式=15a2b-5ab2+4ab2-12a2b=3a2b-ab2;
③原式=9a2-1.5ab+5b2-7a2+13ab-7b2=2a2-76ab-2b2,
当a=-12,b=1时,原式=-1112.
【解答】
解:①原式=4x+3y-52x=32x+3y;
②原式=15a2b-5ab2+4ab2-12a2b=3a2b-ab2;
③原式=9a2-1.5ab+5b2-7a2+13ab-7b2=2a2-76ab-2b2,
当a=-12,b=1时,原式=-1112.
22.
【答案】
解:6mx2+4nxy+2x+2xy-x2+y+4
=(6m-1)x2+(4n+2)xy+2x+y+4,
由结果中不含二次项,
得到6m-1=0,4n+2=0,即m=16,n=-12,
则多项式2m2n+10m-4n+2-2m2n-4m+2n
=6m-2n+2=1+1+2=4.
【解答】
解:6mx2+4nxy+2x+2xy-x2+y+4
=(6m-1)x2+(4n+2)xy+2x+y+4,
由结果中不含二次项,
得到6m-1=0,4n+2=0,即m=16,n=-12,
则多项式2m2n+10m-4n+2-2m2n-4m+2n
=6m-2n+2=1+1+2=4.
23.
【答案】
13x,4ab,y,8a3x,-1;x-7,x+13,x7+y7,x2+x2+1;13x,4ab,y,8a3x,-1,x-7,x+13,x7+y7,x2+x2+1
【解答】
单项式有:13x,4ab,y,8a3x,-1;
多项式有:x-7,x+13,x7+y7,x2+x2+1;
整式有:13x,4ab,y,8a3x,-1,x-7,x+13,x7+y7,x2+x2+1.
24.
【答案】
由题意得
2x+3(5000-x)=-x+15000,
即每天的生产成本为:(-x+15000)元;
(2.3-2)x+(3.5-3)(5000-x)=-0.2x+2500,
即每天获得的利润为:(-0.2x+2500)元;
当x=2000时,-x+15000=-2000+15000=13000(元),
-0.2x+2500=-0.2×2000+2500=2100(元).
答:当x=2000时,每天的生产成本为13000元,每天获得的利润为2100元.
【解答】
由题意得
2x+3(5000-x)=-x+15000,
即每天的生产成本为:(-x+15000)元;
(2.3-2)x+(3.5-3)(5000-x)=-0.2x+2500,
即每天获得的利润为:(-0.2x+2500)元;
当x=2000时,-x+15000=-2000+15000=13000(元),
-0.2x+2500=-0.2×2000+2500=2100(元).
答:当x=2000时,每天的生产成本为13000元,每天获得的利润为2100元.
25.
【答案】
20,42
n(n+1),(n+2)(n+3)
(3)当n=9时,共有白色瓷砖90块,黑色瓷砖42块,
共需90×4+42×5=570元.
【解答】
解:图形发现:
第1个图形中有白色瓷砖1×2块,共有瓷砖3×4块;
第2个图形中有白色瓷砖2×3块,共有瓷砖4×5块;
第3个图形中有白色瓷砖3×4块,共有瓷砖5×6块;
…(1)第4个图形中有白色瓷砖4×5=20块,共有瓷砖6×7=42块;
(2)第n个图形中有白色瓷砖n(n+1)块,共有瓷砖(n+2)(n+3)块;
(3)当n=9时,共有白色瓷砖90块,黑色瓷砖42块,
共需90×4+42×5=570元.
26.
【答案】
解:(1)由题意可得:30×40%a+40×30%b=(12a+12b)元;
(2)他这次买卖亏本;
理由:270×a+b2-(30a+40b)=5(a-b)
∵ a∴ 5(a-b)<0,
∴ 他这次买卖是亏本.
【解答】
解:(1)由题意可得:30×40%a+40×30%b=(12a+12b)元;
(2)他这次买卖亏本;
理由:270×a+b2-(30a+40b)=5(a-b)
∵ a∴ 5(a-b)<0,
∴ 他这次买卖是亏本.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列各式中是代数式的是( )
A.a2-b2=0 B.4>3 C.a D.5x-2≠0
?
2. 下列说法正确的有( )个
①-25πxy2的系数为-25;②1是单项式;③2x-5是多项式;④单项式(-2)2x2y3的次数为7.
A.3 B.4 C.2 D.1
?
3. 用代数式表示“a、b两数的平方和减去它们乘积的2倍”,正确的是( )
A.a2+b2-2ab B.(a+b)2-2ab C.a2b2-2ab D.2(a2+b2-ab)
?
4. 下面的说法正确的是( )
A.单项式2πa2b的次数是4次 B.多项式a2b+bc+3的次数是2
C.3ab5的系数是3 D.x+1x+4不是多项式
?5. 在式子2ab,mn2+2m3,x,y+zx,0,5π,-2πpq3中单项式有( )
A.6个 B.5个 C.4个 D.3个
?
6. 下列式子中:12,3ab,m+2n,2x+3=1,st,整式的个数为( )
A.2个 B.3个 C.4个 D.5个
?
7. 下列式子中:13,1x+2,x3-y,π(x2-y2),16a2,7x-1,y2+8x,9a2+1a-2,单项式和多项式的个数分别为( )
A.2个,5个 B.2个,4个 C.3个,4个 D.2个,6个
?
8. 下列运算中,正确的是( )
A.3a+2b=5ab B.2a3+3a2=5a5 C.5a2-4a2=1 D.3a2b-3ba2=0
?
9. 下列说法正确的是( )
A.-33a2bc2的系数为-3,次数为27
B.xπ+y2+z23不是单项式,但是整式
C.1x+1是多项式
D.mx2+1一定是关于x的二次二项式
?
10. 如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第8层中含有正三角形个数是( )
A.54个 B.90个 C.102个 D.114个
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 如果a-b-2=0,那么代数式1-2a+2b的值是________.
?
12. 化简:3+[3a-2(a-1)]=________.
?
13. 若3xm-2yn+3与-5x5y2是同类项,则m+n=________.
?
14. 观察下列各式1×3=3=22-1,3×5=15=42-1,5×7=35=62-1,11×13=143=122-1…把你猜想到的规律用只含一个字母的等式表示出来________.
?15. 某班有女生a人,男生比女生的2倍少5人,则男生有________人.
?
16. 若x2-2x-2的值为0,则3x2-6x的值是________.
?
17. 若单项式12x2ym与-2xny3是同类项,则m=________,n=________.
?
18. 代数式-πa2b22的系数是________,次数是________.
?
19. 已知5x3ym与6xny2可以合并为一项,则mn的值是________.
?
20. 多项式12x|m|-(m+2)x+7是关于x的二次三项式,则m=________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 化简或求值:
①4x-(-3y+52x);?????????????????②5(3a2b-ab2)-4(-ab2+3a2b);
③(9a2-1.5ab+5b2)-(7a2-13ab+7b2),其中a=-12,b=1.
?
22. 关于x,y的多项式6mx2+4nxy+2x+2xy-x2+y+4不含二次项,求多项式2m2n+10m-4n+2-2m2n-4m+2n的值.
?
23. 把下列各式填在相应的大括号里:
x-7,13x,4ab,23a,5-3x,y,st,x+13,x7+y7,x2+x2+1,m-1m+1,8a3x,-1
单项式集合{?...};
多项式集合{?...};
整式集合{?...}.
?
24. 自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天生产5000个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋x个.
成本(元/个)
售价(元/个)
A
2
2.3
B
3
3.5
(1)用含x的式子表示每天的生产成本和每天获得的利润;
(2)当x=2000时,求每天的生产成本和每天获得的利润.
?
25. 如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题.
(1)在第4个图中,白色瓷砖共有________块,一共有瓷砖________块;
(2)在第n个图中,黑色瓷砖共有________块,一共有瓷砖________块;
(3)如果每块黑瓷砖5元,白瓷砖4元,铺设当n=9时,共需花多少钱购买瓷砖?
?26. 李师傅下岗后,做起来小生意,第一次进货,他以每件a元的价格购进了30件甲种小商品,以每件b元的价格购进了40件乙种小商品,且a
(2)若李师傅将两种商品都以a+b2元的价格全部出售,他这次买卖是赚钱还是亏本,请说明理由?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:A:a2-b2=0为等式,不为代数式,故本项错误.
B:4>3为不等式,故本项错误.
C;a为代数式,故本项正确.
D:5x-2≠0为不等式,故本项错误.
故选:C.
2.
【答案】
D
【解答】
解:①-25πxy2的系数为-25π,故①错误;
②1是单项式,故②正确;
③2x不是单项式,所以2x-5不是多项式,故③错误;
④单项式(-2)2x2y3的次数为5,故④错误;
故选(D)
3.
【答案】
A
【解答】
解:a、b两数的平方和是a2+b2,
它们乘积的2倍是2ab,
则a、b两数的平方和减去它们乘积的2倍是:a2+b2-2ab;
故选A.
4.
【答案】
D
【解答】
解:A、单项式2πa2b的次数是3次,故选项错误;
B、多项式a2b+bc+3的次数是3,故选项错误;
C、3ab5的系数是35,故选项错误;
D、x+1x+4不是多项式是正确的.
故选D.
5.
【答案】
B
【解答】
解:2ab是单项式;
mn2+2m3含有加减运算是多项式;
x单独一个字母是一个单项式;
y+zx分母含有字母既不是单项式,也不是多项式;
0、5π都数字是一个单项式;
-2πpq3是单项式.
共有5个单项式.
故选:B.
6.
【答案】
B
【解答】
解:由整式的概念可得,12,3ab,m+2n是整式,
2x+3=1是等式不是整式,
st是分式不是整式.
故选B.
7.
【答案】
B
【解答】
解:所给式子中单项式有13,16a2一共2个;
多项式有:1x+2,x3-y,π(x2-y2),7x-1,y2+8x,一共4个.
故选B.
8.
【答案】
D
【解答】
解:A、不是同类项不能合并,故A错误;
B、合并同类项系数相加字母及指数不变,故B错误;
C、合并同类项系数相加字母及指数不变,故C错误;
D、合并同类项系数相加字母及指数不变,故D正确;
故选:D.
9.
【答案】
B
【解答】
解:A、-33a2bc2的系数为-33,次数为2+1+2=5,所以此选项不正确;
B、xπ+y2+z23不是单项式,是多项式,是整式,所以此选项正确;
C、1x+1不是多项式,是分式,所以此选项不正确;
D、因为m不确定,当m=0时,mx2+1=1,是单项式,当m≠0时,一定是关于x的二次二项式,所以此选项不正确.
故选B.
10.
【答案】
B
【解答】
根据题意分析可得:从里向外的第1层包括6个正三角形.第2层包括18个正三角形.此后,每层都比前一层多12个.依此递推,第8层中含有正三角形个数是6+12×7=90个.
故选:B.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
-3
【解答】
∵ a-b-2=0,
∴ a-b=2,
则原式=1-2(a-b)
=1-2×2
=1-4
=-3,
12.
【答案】
a+5
【解答】
解:原式=3+3a-2a+2=a+5,
故答案为:a+5
13.
【答案】
6
【解答】
解:∵ 3xm-2yn+3与-5x5y2是同类项,
∴ m-2=5n+3=2,
解得:m=7n=-1,
则m+n=7+(-1)=6.
故答案为:6.
14.
【答案】
(n-1)(n+1)=n2-1
【解答】
解:∵ 1×3=3=22-1,3×5=15=42-1,5×7=35=62-1,11×13=143=122-1…,
∴ 规律为:(n-1)(n+1)=n2-1.
故答案为:(n-1)(n+1)=n2-1.
15.
【答案】
(2a-5)
【解答】
解:依题意得:(2a-5).
16.
【答案】
6
【解答】
解:由x2-2x-2=0,
得到x2-2x=2,
则原式=3(x2-2x)=6.
故答案为:6.
17.
【答案】
3,2
【解答】
解:∵ 单项式12x2ym与-2xny3是同类项,
∴ n=2,m=3,
故答案为:3、2.
18.
【答案】
-12π,4
【解答】
解:代数式-πa2b22的系数是-12π,次数是4.
故答案为:-12π,4.
19.
【答案】
【解答】
此题暂无解答
20.
【答案】
2
【解答】
∵ 多项式是关于x的二次三项式,
∴ |m|=2,
∴ m=±2,
但-(m+2)≠0,
即m≠-2,
综上所述,m=2,故填空答案:2.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:①原式=4x+3y-52x=32x+3y;
②原式=15a2b-5ab2+4ab2-12a2b=3a2b-ab2;
③原式=9a2-1.5ab+5b2-7a2+13ab-7b2=2a2-76ab-2b2,
当a=-12,b=1时,原式=-1112.
【解答】
解:①原式=4x+3y-52x=32x+3y;
②原式=15a2b-5ab2+4ab2-12a2b=3a2b-ab2;
③原式=9a2-1.5ab+5b2-7a2+13ab-7b2=2a2-76ab-2b2,
当a=-12,b=1时,原式=-1112.
22.
【答案】
解:6mx2+4nxy+2x+2xy-x2+y+4
=(6m-1)x2+(4n+2)xy+2x+y+4,
由结果中不含二次项,
得到6m-1=0,4n+2=0,即m=16,n=-12,
则多项式2m2n+10m-4n+2-2m2n-4m+2n
=6m-2n+2=1+1+2=4.
【解答】
解:6mx2+4nxy+2x+2xy-x2+y+4
=(6m-1)x2+(4n+2)xy+2x+y+4,
由结果中不含二次项,
得到6m-1=0,4n+2=0,即m=16,n=-12,
则多项式2m2n+10m-4n+2-2m2n-4m+2n
=6m-2n+2=1+1+2=4.
23.
【答案】
13x,4ab,y,8a3x,-1;x-7,x+13,x7+y7,x2+x2+1;13x,4ab,y,8a3x,-1,x-7,x+13,x7+y7,x2+x2+1
【解答】
单项式有:13x,4ab,y,8a3x,-1;
多项式有:x-7,x+13,x7+y7,x2+x2+1;
整式有:13x,4ab,y,8a3x,-1,x-7,x+13,x7+y7,x2+x2+1.
24.
【答案】
由题意得
2x+3(5000-x)=-x+15000,
即每天的生产成本为:(-x+15000)元;
(2.3-2)x+(3.5-3)(5000-x)=-0.2x+2500,
即每天获得的利润为:(-0.2x+2500)元;
当x=2000时,-x+15000=-2000+15000=13000(元),
-0.2x+2500=-0.2×2000+2500=2100(元).
答:当x=2000时,每天的生产成本为13000元,每天获得的利润为2100元.
【解答】
由题意得
2x+3(5000-x)=-x+15000,
即每天的生产成本为:(-x+15000)元;
(2.3-2)x+(3.5-3)(5000-x)=-0.2x+2500,
即每天获得的利润为:(-0.2x+2500)元;
当x=2000时,-x+15000=-2000+15000=13000(元),
-0.2x+2500=-0.2×2000+2500=2100(元).
答:当x=2000时,每天的生产成本为13000元,每天获得的利润为2100元.
25.
【答案】
20,42
n(n+1),(n+2)(n+3)
(3)当n=9时,共有白色瓷砖90块,黑色瓷砖42块,
共需90×4+42×5=570元.
【解答】
解:图形发现:
第1个图形中有白色瓷砖1×2块,共有瓷砖3×4块;
第2个图形中有白色瓷砖2×3块,共有瓷砖4×5块;
第3个图形中有白色瓷砖3×4块,共有瓷砖5×6块;
…(1)第4个图形中有白色瓷砖4×5=20块,共有瓷砖6×7=42块;
(2)第n个图形中有白色瓷砖n(n+1)块,共有瓷砖(n+2)(n+3)块;
(3)当n=9时,共有白色瓷砖90块,黑色瓷砖42块,
共需90×4+42×5=570元.
26.
【答案】
解:(1)由题意可得:30×40%a+40×30%b=(12a+12b)元;
(2)他这次买卖亏本;
理由:270×a+b2-(30a+40b)=5(a-b)
∵ a
∴ 他这次买卖是亏本.
【解答】
解:(1)由题意可得:30×40%a+40×30%b=(12a+12b)元;
(2)他这次买卖亏本;
理由:270×a+b2-(30a+40b)=5(a-b)
∵ a
∴ 他这次买卖是亏本.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
