3.2.2 代数式(2)(共21张PPT)
文档属性
| 名称 | 3.2.2 代数式(2)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 13:35:18 | ||
图片预览







文档简介
3.2.2 代数式(2)
第三章 整式及其加减
2020-2021北师大版七年级数学上册
1.会求代数式的值并解释代数式值的实际意义.(重点)
2.利用代数式求值推断代数式所反应的规律.
(难点)
学习目标
据报纸记载,一位医生研究得出由父母身高预测子女成年后身高的公式:儿子身高是由父母身高的和的一半,再乘以1.08;女儿的身高是父亲身高的0.923倍加上母亲身高的和再除以2.
新课导入
(1)已知父亲身高是a米,母亲身高是b米,试用代数式表示儿子和女儿的身高;
(2)五年级女生小红的父亲身高是1.75米,母亲的身高是1.62米;六年级男生小明的父亲的身高是1.70,母亲的身高是1.62,试预测成年以后小明与小红谁个子高?
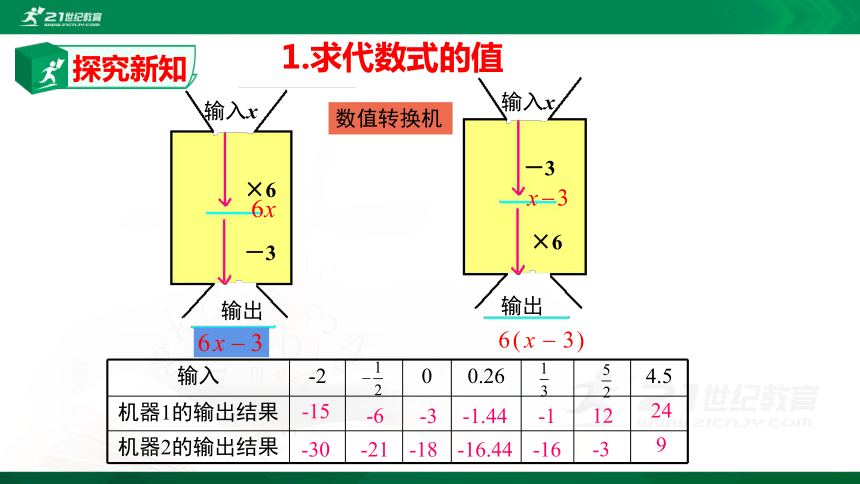
1.求代数式的值
数值转换机
输入
-2
0
0.26
4.5
机器1的输出结果
机器2的输出结果
输入x
输入x
输出
输出
×6
-3
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
×6
-3
探究新知
n
1
2
3
4
5
6
7
8
5n+6
n2
11
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
逐渐增大
n2 先超过100
填写下表,并观察下列两个代数式的值的变化情况.
典例讲解
【总结】 代数式的值是由其所含的字母的取值所确定的,并随字母取值的变化而变化,字母取不同的值时,代数式的值可能不同,也可能相同.
例2.当x=2,y=-3时,求代数式 x(x-y) 的值
解:当x=2,y=-3时
x(x-y) = 2×[2-(-3)]
=2 ×5
=10
省略的“×”号
要恢复“×”号
字母用负数来替代时,负数要添上括号。并且注意改变原来的括号。
典例讲解
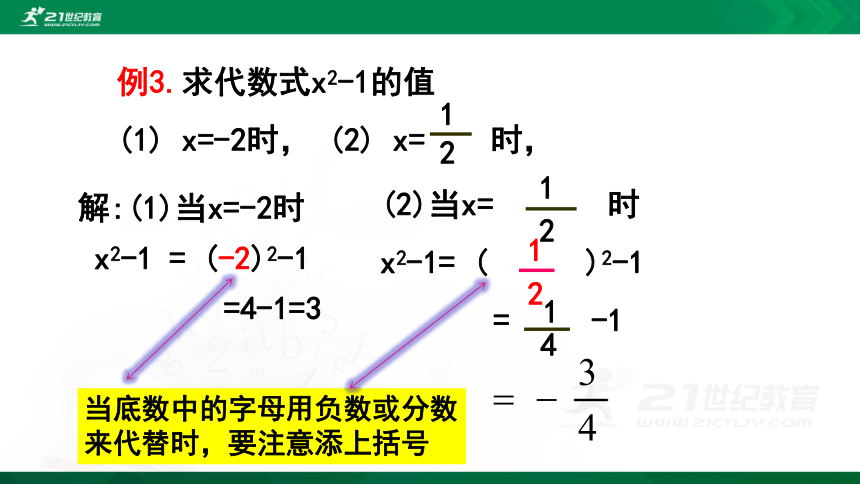
解:(1)当x=-2时
x2-1 = (-2)2-1
=4-1=3
1
2
(2)当x= 时
x2-1= ( )2-1
= -1
1
2
1
2
1
4
当底数中的字母用负数或分数来代替时,要注意添上括号
例3.求代数式x2-1的值
(1) x=-2时, (2) x= 时,
一、求代数式的值的步骤:
(1)代入,将字母所取的值代入代数式中;
(2)计算,按照代数式指明的运算进行,计算出结果
二、注意的几个问题:
(1)由于代数式的值是由代数式中的字母所取的值确定的,所以代入数值前应先指明字母的取值,把“当……时”写出来。
(2)如果字母的值是负数、分数,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号。
求代数式的值方法归纳:
归纳小结
2.整体代入求值
探究新知
例5.若 的值为7,求代数式 的值。
解:由 , 得
=3 +4
(逆用乘法分配律)
1.已知 则 的值是多少?
解:
由
可得
将
代入上式:
2.当x=1时,代数式 ,当x=-1时,该代数式的值是多少?
解:将x=1代入代数式,得a+b=2017,当x=-1时,
及时训练
3.辅助未知数法求值
1.已知 ,求 的值.
2.已知 ,求 的值.
已知几个字母的比值时,设每份为k
探究新知
2.如果2a+3b=5,那么4a+6b-7=__.
3
3.已知a+b=5,ab=6 ,则ab-(a+b)=___.
1
4.如图所示是一数值转换机,若输入的x为-5,则输出的结果为_______.
49
课堂练习
1.已知a,b 互为相反数,c,d 互为倒数,则2(a+b)-3cd的值为________.
-3
5.当x=-3,y=2时,求下列代数式的值:
解:
当x=-3,y=2时
6.已知 b=2,求代数式 的值.
解:当 b=2时,
7.物体自由下落的高度 h( m)和下落时间 t( s)的关系,在地球上大约是:h = 4.9 t2,在月球上大约是:h = 0.8 t2.
(1)填写下表:
{7DF18680-E054-41AD-8BC1-D1AEF772440D}t
0
2
4
6
8
10
h = 4.9 t2
h = 0.8 t2
0
0
19.6
3.2
78.4
12.8
176.4
28.8
313.6
51.2
490
80
(2)物体在哪儿下落得快?
(3) 当 h = 20 m 时,比较物体在地球上和在月球上自由下落所需的时间.
(2)物体在地球上下落得快;
(3) 把 h = 20 m 分别代入h=4.9t2和h=0.8t2,得t(地球)≈2(s),t(月球)=5(s).
用具体数值代替代数式里的字母,按照代数式指明的运算计算出的结果叫代数式的值.
课堂小结
谢谢聆听
第三章 整式及其加减
2020-2021北师大版七年级数学上册
1.会求代数式的值并解释代数式值的实际意义.(重点)
2.利用代数式求值推断代数式所反应的规律.
(难点)
学习目标
据报纸记载,一位医生研究得出由父母身高预测子女成年后身高的公式:儿子身高是由父母身高的和的一半,再乘以1.08;女儿的身高是父亲身高的0.923倍加上母亲身高的和再除以2.
新课导入
(1)已知父亲身高是a米,母亲身高是b米,试用代数式表示儿子和女儿的身高;
(2)五年级女生小红的父亲身高是1.75米,母亲的身高是1.62米;六年级男生小明的父亲的身高是1.70,母亲的身高是1.62,试预测成年以后小明与小红谁个子高?
1.求代数式的值
数值转换机
输入
-2
0
0.26
4.5
机器1的输出结果
机器2的输出结果
输入x
输入x
输出
输出
×6
-3
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
×6
-3
探究新知
n
1
2
3
4
5
6
7
8
5n+6
n2
11
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
逐渐增大
n2 先超过100
填写下表,并观察下列两个代数式的值的变化情况.
典例讲解
【总结】 代数式的值是由其所含的字母的取值所确定的,并随字母取值的变化而变化,字母取不同的值时,代数式的值可能不同,也可能相同.
例2.当x=2,y=-3时,求代数式 x(x-y) 的值
解:当x=2,y=-3时
x(x-y) = 2×[2-(-3)]
=2 ×5
=10
省略的“×”号
要恢复“×”号
字母用负数来替代时,负数要添上括号。并且注意改变原来的括号。
典例讲解
解:(1)当x=-2时
x2-1 = (-2)2-1
=4-1=3
1
2
(2)当x= 时
x2-1= ( )2-1
= -1
1
2
1
2
1
4
当底数中的字母用负数或分数来代替时,要注意添上括号
例3.求代数式x2-1的值
(1) x=-2时, (2) x= 时,
一、求代数式的值的步骤:
(1)代入,将字母所取的值代入代数式中;
(2)计算,按照代数式指明的运算进行,计算出结果
二、注意的几个问题:
(1)由于代数式的值是由代数式中的字母所取的值确定的,所以代入数值前应先指明字母的取值,把“当……时”写出来。
(2)如果字母的值是负数、分数,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号。
求代数式的值方法归纳:
归纳小结
2.整体代入求值
探究新知
例5.若 的值为7,求代数式 的值。
解:由 , 得
=3 +4
(逆用乘法分配律)
1.已知 则 的值是多少?
解:
由
可得
将
代入上式:
2.当x=1时,代数式 ,当x=-1时,该代数式的值是多少?
解:将x=1代入代数式,得a+b=2017,当x=-1时,
及时训练
3.辅助未知数法求值
1.已知 ,求 的值.
2.已知 ,求 的值.
已知几个字母的比值时,设每份为k
探究新知
2.如果2a+3b=5,那么4a+6b-7=__.
3
3.已知a+b=5,ab=6 ,则ab-(a+b)=___.
1
4.如图所示是一数值转换机,若输入的x为-5,则输出的结果为_______.
49
课堂练习
1.已知a,b 互为相反数,c,d 互为倒数,则2(a+b)-3cd的值为________.
-3
5.当x=-3,y=2时,求下列代数式的值:
解:
当x=-3,y=2时
6.已知 b=2,求代数式 的值.
解:当 b=2时,
7.物体自由下落的高度 h( m)和下落时间 t( s)的关系,在地球上大约是:h = 4.9 t2,在月球上大约是:h = 0.8 t2.
(1)填写下表:
{7DF18680-E054-41AD-8BC1-D1AEF772440D}t
0
2
4
6
8
10
h = 4.9 t2
h = 0.8 t2
0
0
19.6
3.2
78.4
12.8
176.4
28.8
313.6
51.2
490
80
(2)物体在哪儿下落得快?
(3) 当 h = 20 m 时,比较物体在地球上和在月球上自由下落所需的时间.
(2)物体在地球上下落得快;
(3) 把 h = 20 m 分别代入h=4.9t2和h=0.8t2,得t(地球)≈2(s),t(月球)=5(s).
用具体数值代替代数式里的字母,按照代数式指明的运算计算出的结果叫代数式的值.
课堂小结
谢谢聆听
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
