2020-2021学年沪科新版八年级上册数学《第15章 轴对称图形与等腰三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年沪科新版八年级上册数学《第15章 轴对称图形与等腰三角形》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 343.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 21:39:29 | ||
图片预览

文档简介
2020-2021学年沪科新版八年级上册数学《第15章
轴对称图形与等腰三角形》单元测试卷
一.选择题
1.现实世界中,对称现象无处不在.下列标志中,不是轴对称图形的是( )
A.
B.
C.
D.
2.如图,有A、B、C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.∠A、∠B两内角的平分线的交点处
B.AC、AB两边高线的交点处
C.AC、AB两边中线的交点处
D.AC、AB两边垂直平分线的交点处
3.已知△ABC的三边a,b,c满足(a﹣4)2++|c﹣4|=0,那么△ABC是( )
A.不等边三角形
B.等边三角形
C.等腰三角形
D.不能判断
4.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角(如:∠1=∠2,∠3=∠4).当小球第1次碰到长方形的边时的点为Q,第2次碰到长方形的边时的点为M…,第2019次碰到长方形的边时的点为图中的( )
A.N点
B.Q点
C.M点
D.P点
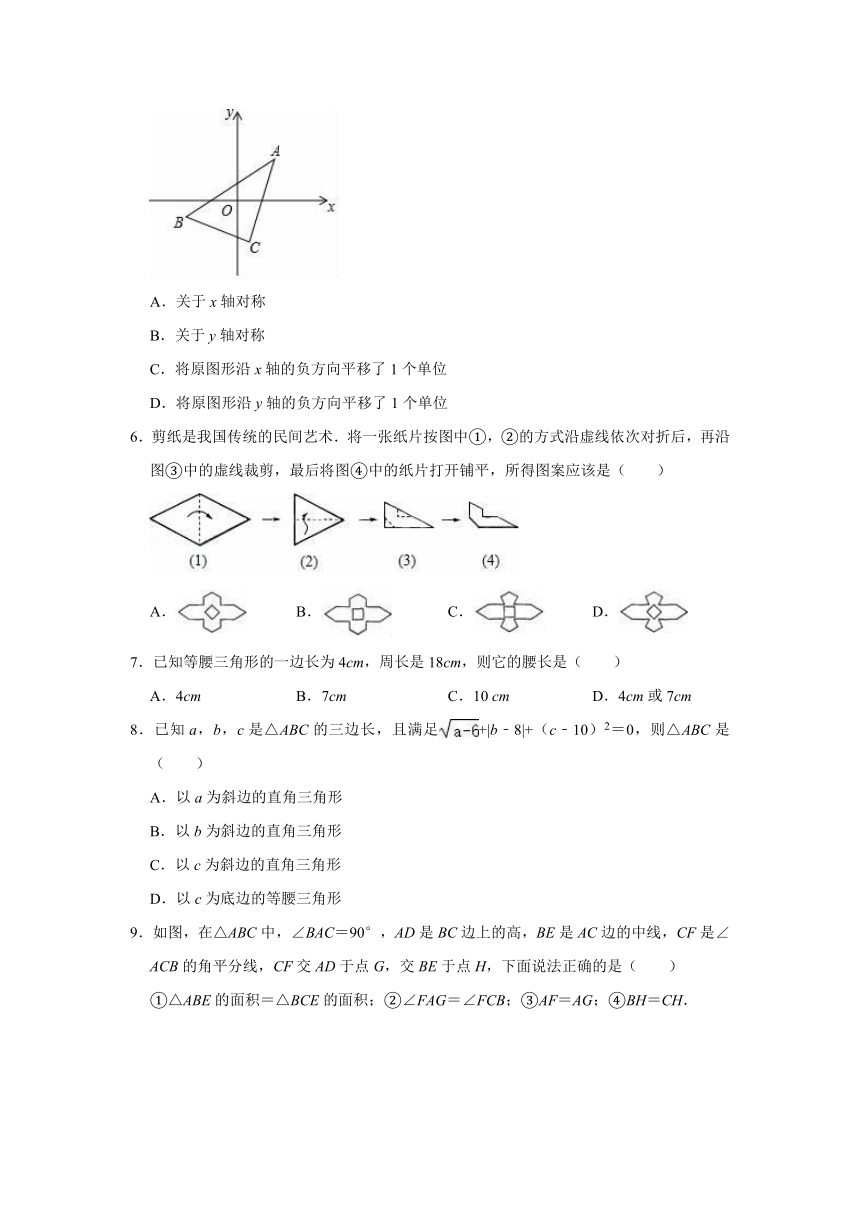
5.如图,保持△ABC的三个顶点的横坐标不变,纵坐标都乘﹣1,画出坐标变化后的三角形,则所得三角形与原三角形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.将原图形沿x轴的负方向平移了1个单位
D.将原图形沿y轴的负方向平移了1个单位
6.剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A.
B.
C.
D.
7.已知等腰三角形的一边长为4cm,周长是18cm,则它的腰长是( )
A.4cm
B.7cm
C.10
cm
D.4cm或7cm
8.已知a,b,c是△ABC的三边长,且满足+|b﹣8|+(c﹣10)2=0,则△ABC是( )
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.以c为底边的等腰三角形
9.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
A.①②③④
B.①②③
C.②④
D.①③
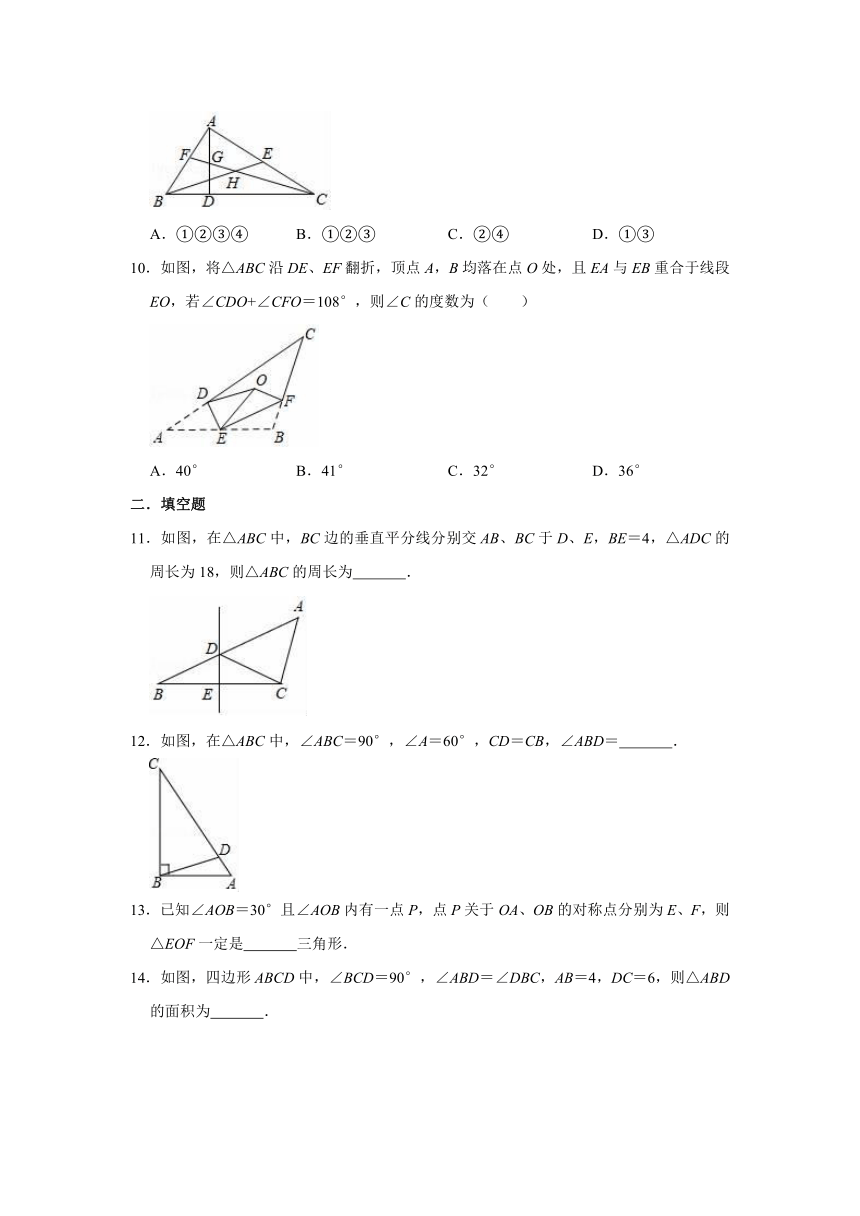
10.如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=108°,则∠C的度数为( )
A.40°
B.41°
C.32°
D.36°
二.填空题
11.如图,在△ABC中,BC边的垂直平分线分别交AB、BC于D、E,BE=4,△ADC的周长为18,则△ABC的周长为
.
12.如图,在△ABC中,∠ABC=90°,∠A=60°,CD=CB,∠ABD=
.
13.已知∠AOB=30°且∠AOB内有一点P,点P关于OA、OB的对称点分别为E、F,则△EOF一定是
三角形.
14.如图,四边形ABCD中,∠BCD=90°,∠ABD=∠DBC,AB=4,DC=6,则△ABD的面积为
.
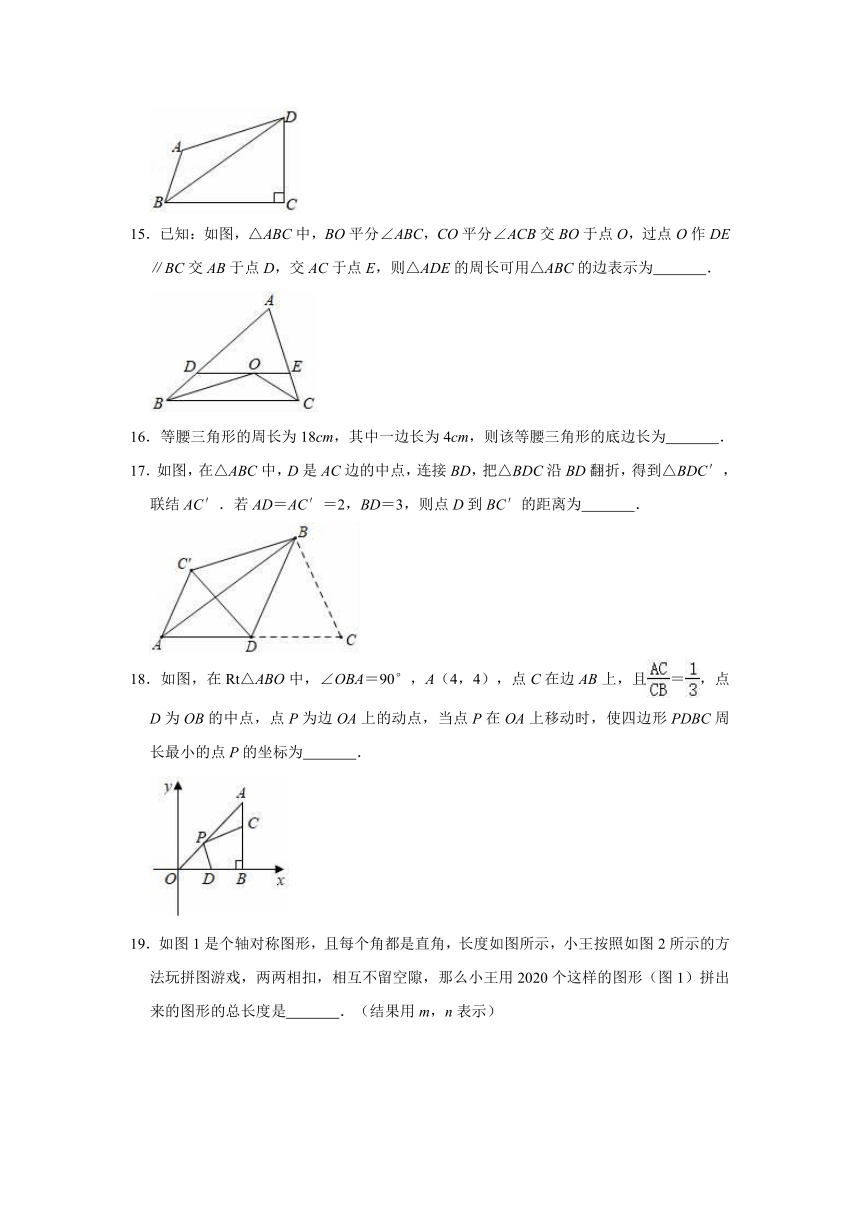
15.已知:如图,△ABC中,BO平分∠ABC,CO平分∠ACB交BO于点O,过点O作DE∥BC交AB于点D,交AC于点E,则△ADE的周长可用△ABC的边表示为
.
16.等腰三角形的周长为18cm,其中一边长为4cm,则该等腰三角形的底边长为
.
17.如图,在△ABC中,D是AC边的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,联结AC′.若AD=AC′=2,BD=3,则点D到BC′的距离为
.
18.如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且=,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为
.
19.如图1是个轴对称图形,且每个角都是直角,长度如图所示,小王按照如图2所示的方法玩拼图游戏,两两相扣,相互不留空隙,那么小王用2020个这样的图形(图1)拼出来的图形的总长度是
.(结果用m,n表示)
20.雨后,地上的积水犹如一块澄澈的平面镜,某路段监控摄像头在雨后拍摄,由于位置偏离,拍摄中心聚集在了水面上,摄像头侦测到一小轿车超速行驶,积水中倒映的车牌为“”,那么该小轿车的真实车牌号为
.
三.解答题
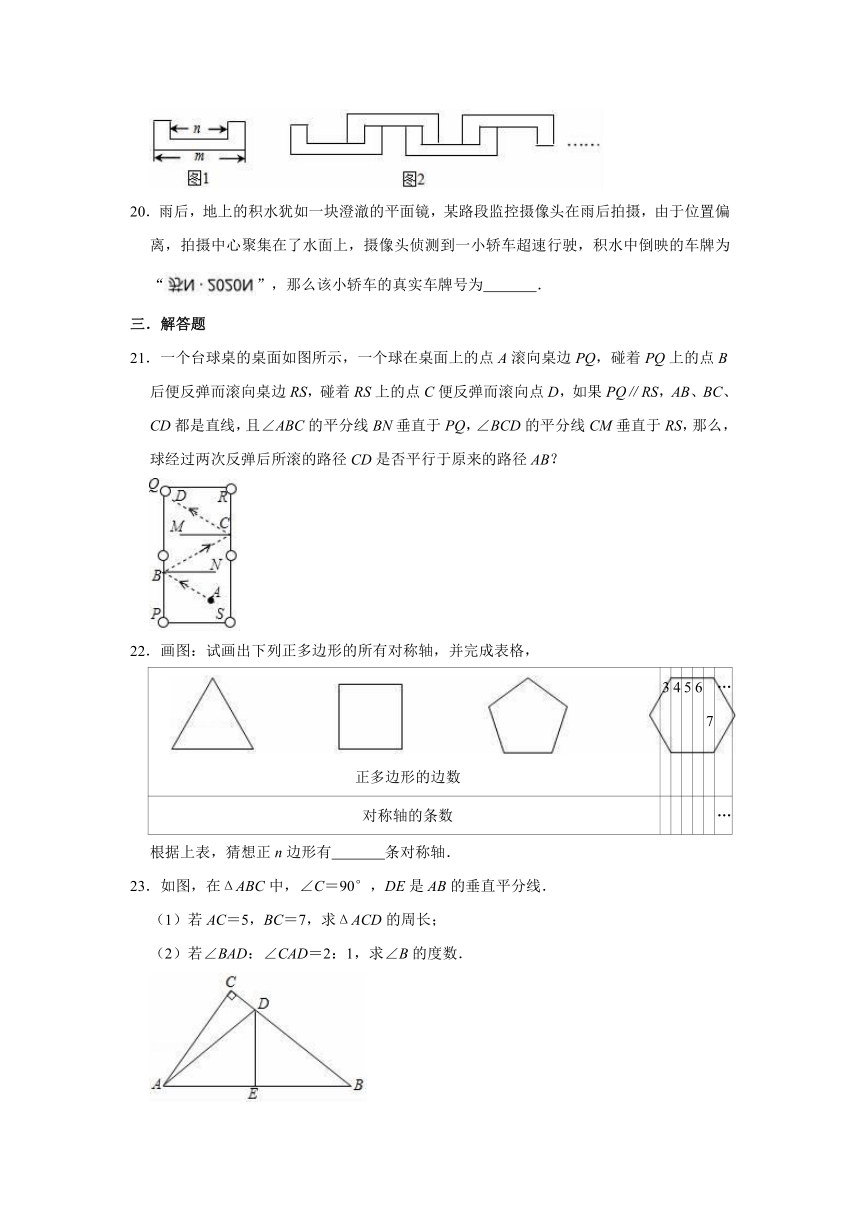
21.一个台球桌的桌面如图所示,一个球在桌面上的点A滚向桌边PQ,碰着PQ上的点B后便反弹而滚向桌边RS,碰着RS上的点C便反弹而滚向点D,如果PQ∥RS,AB、BC、CD都是直线,且∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,那么,球经过两次反弹后所滚的路径CD是否平行于原来的路径AB?
22.画图:试画出下列正多边形的所有对称轴,并完成表格,
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有
条对称轴.
23.如图,在ΔABC中,∠C=90°,DE是AB的垂直平分线.
(1)若AC=5,BC=7,求ΔACD的周长;
(2)若∠BAD:∠CAD=2:1,求∠B的度数.
24.如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG=
;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=x°,过点C作CF∥OA交AB于点F,求∠BGO﹣∠ACF的度数.(用含x的代数式表示)
25.如图,在已知的平面直角坐标系中,AABC的顶点都在正方形网格的格点上,若点A、B、C的坐标分别是A(﹣2,1),B(﹣3,3),C(﹣1,4).
(1)画出△ABC关于x轴对称的图形△A1B1C1,并写出此时B1的坐标是:
.
(2)画出△ABC沿x轴正方向平移3个单位,再沿y轴负方向平移2个单位的图形△A2B2C2.
(3)△ABC的面积.
26.已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.求证:△OCD是等边三角形.
27.已知,如图,AB=AC,BO、CO分别是∠ABC和∠ACB的平分线,联结AO并延长交BC于点D,求证:AD⊥BC.
参考答案与试题解析
一.选择题
1.解:A、是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项符合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不合题意;
故选:B.
2.解:根据线段垂直平分线上的点到线段两个端点的距离相等,超市应建在AC、AB两边垂直平分线的交点处,
故选:D.
3.解:∵(a﹣4)2++|c﹣4|=0,
∴a﹣4=0,b﹣4=0,c﹣4=0,
∴a=b=c=4,
∴△ABC的形状是等边三角形,
故选:B.
4.解:如图所示,经过6次反弹后动点回到出发点P,
∵2019÷6=336…3,
∴当点P第2019次碰到矩形的边时为第337个循环组的第3次反弹,
∴第2019次碰到矩形的边时的点为图中的点N,
故选:A.
5.解:∵纵坐标乘以﹣1,
∴变化前后纵坐标互为相反数,
又∵横坐标不变,
∴所得三角形与原三角形关于x轴对称.
故选:A.
6.解:按照图中的顺序,向右对折,向上对折,从斜边处剪去一个直角三角形,从直角顶点处剪去一个等腰直角三角形,展开后实际是从原菱形的四边处各剪去一个直角三角形,从菱形的中心剪去一个正方形,可得:
.
故选:A.
7.解:分情况考虑:当4是腰时,则底边长是18﹣8=10,此时4,4,10不能组成三角形,应舍去;
当4是底边时,腰长是(18﹣4)×=7,
4,7,7能够组成三角形.此时腰长是7.
故选:B.
8.解:由题意得,a﹣6=0,b﹣8=0,c﹣10=0,
解得a=6,b=8,c=10,
∵62+82=100=102,
∴a2+b2=c2,
∴∠ACB=90°,
故选:C.
9.解:∵BE是AC边的中线,
∴AE=CE,
∵△ABE的面积=,△BCE的面积=AB,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=180°﹣∠BAC﹣∠ACF,∠AGF=∠DGC=180°﹣∠ADC﹣∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故④错误;
即正确的为①③,
故选:D.
10.解:如图所示,连接CO并延长,
设∠ACB=α,则∠A+∠B=180°﹣α,
由折叠可得,∠DOE=∠A,∠FOE=∠B,
∴∠DOF=∠A+∠B=180°﹣α,
∵∠DOG是△COD的外角,
∴∠DOG=∠DCO+∠CDO,
同理可得,∠FOG=∠FCO+∠CFO,
∴∠DOF=ACB+∠CDO+∠CFO,
即180°﹣α=α+108°,
解得α=36°,
∴∠ACB=36°,
故选:D.
二.填空题
11.解:∵DE是线段BC的垂直平分线,BE=4,
∴DB=DC,BC=2BE=8,
∵△ADC的周长为18,
∴AC+AD+DC=18,
∴AC+AD+DB=AC+AB=18,
∴△ABC的周长=AC+AB+BC=26,
故答案为:26.
12.解:∵∠ABC=90°,∠A=60°,
∴∠C=90°﹣∠A=90°﹣60°=30°,
∵CD=CB,
∴∠CBD=(180°﹣∠C)=(180°﹣30°)=75°,
∴∠ABD=∠ABC﹣∠CBD
=90°﹣75°
=15°.
故答案为:15°.
13.解:如图.连接OP,OE,OF.
∵点P关于OA的对称点为E,
∴OA是PE的垂直平分线,
∴OP=OE;
同理OF=OP,
∴OE=OF.
∴△EOF是等腰三角形.
∵∠AOB=30°,
∴∠EOF=60°,
∴等腰△EOF是等边三角形.
14.解:过D作DE⊥BA,交BA的延长线于E,
∵∠BCD=90°,∠ABD=∠DBC,
∴DE=DC,
∵DC=6,
∴DE=6,
∵AB=4,
∴△ABD的面积是==12,
故答案为:12.
15.解:∵BO平分∠ABC,CO平分∠ACB,
∴∠DBO=∠OBC,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠OBC,∠COE=∠OCB,
∴∠DOB=∠DBO,∠EOC=∠OCE,
∴BD=DO,OE=CE,
∴△ADE的周长=AD+DO+OE+AE=AD+DB+AE+EC=AB+AC
故答案为:AB+AC.
16.解:当4cm为底边长时,腰长为(18﹣4)÷2=7(cm),
当4cm为腰长时,底边长为18﹣4×2=10(cm),
∵4+4<10,
∴当4cm为腰长时,不能组成三角形,
∴该等腰三角形的底边长为4cm,
故答案为4cm.
17.解:如图,连接CC',交BD于点M,过点D作DH⊥BC'于点H,
∵AD=AC′=2,D是AC边上的中点,
∴DC=AD=2,
由翻折知,△BDC≌△BDC',BD垂直平分CC',
∴DC=DC'=2,BC=BC',CM=C'M,
∴AD=AC′=DC'=2,
∴△ADC'为等边三角形,
∴∠ADC'=∠AC'D=∠C'AC=60°,
∵DC=DC',
∴∠DCC'=∠DC'C=×60°=30°,
在Rt△C'DM中,
∠DC'C=30°,DC'=2,
∴DM=1,C'M=DM=,
∴BM=BD﹣DM=3﹣1=2,
在Rt△BMC'中,
BC'===,
∵S△BDC'=BC'?DH=BD?CM,
∴DH=3×,
∴DH=,
∵∠DCB=∠DBC',
∴点D到BC的距离为.
故答案为:.
18.解:∵在Rt△ABO中,∠OBA=90°,A(4,4),
∴AB=OB=4,∠AOB=45°,
∵=,点D为OB的中点,
∴BC=3,OD=BD=2,
∴D(2,0),C(4,3),
作D关于直线OA的对称点E,连接EC交OA于P,
则此时,四边形PDBC周长最小,E(0,2),
∵直线OA
的解析式为y=x,
设直线EC的解析式为y=kx+b,
∴,
解得:,
∴直线EC的解析式为y=x+2,
解得,,
∴P(,),
故答案为:(,).
19.解:由图可得,2个这样的图形(图1)拼出来的图形中,重叠部分的长度为m﹣n,
∴用2020个这样的图形(图1)拼出来的图形的总长度=2020m﹣2019(m﹣n)=m+2019n,
故答案为:m+2019n.
20.解:利用轴对称的性质得出:
该汽车牌照号码为:苏N?2020N.
故答案为:苏N?2020N.
三.解答题
21.解:球经过两次反弹后所滚的路径CD平行于原来的路径AB.理由如下:
∵PQ∥RS,∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,
∴BN∥CM,
∴∠CBN=∠BCM,
又∵∠ABC=2∠CBN,∠BCD=2∠BCM,
∴∠ABC=∠BCD,
∴CD∥AB.
22.解:如图,
故填3,4,5,6,7,n.
23.解:(1)∵DE是AB的垂直平分线,
∴DA=DB,
∴ΔACD的周长=AC+CD+DA=AC+CD+DB+AC+CB=5+7=12;
(2)∵DA=DB,
∴∠BAD=∠B,
设∠CAD=x,则∠BAD=∠B=2x,
∵∠C=90°,
∴∠CAB+∠B=90°,即x+2x+2x=90°,
解得,x=18°,
∴∠B=2x=36°.
24.解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°﹣n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°﹣n°,
∴∠ACG=∠CBA+∠CAB=90°﹣n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO﹣∠ACF=∠BGO﹣∠CAG=∠ACG=90°﹣x°.
25.解:(1)如图所示,△A1B1C1即为所求,此时B1的坐标是(﹣3,﹣3),
故答案为:(﹣3,﹣3).
(2)如图所示,△A2B2C2即为所求,
(3)△ABC的面积为2×3﹣×1×3﹣×1×2﹣1×2=2.5.
26.证明:∵△ABO是等边三角形,
∴∠A=∠B=∠AOB=60°,
∵AB∥CD,
∴∠C=∠A=60°,∠D=∠B=60°,
∴∠COD=∠AOB=60°,
∴△OCD是等边三角形.
27.证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BO、CO分别是∠ABC和∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=ACB,
∴∠OBC=∠OCB,
∴OB=OC,
∴点O在线段BC的垂直平分线上,
∵AB=AC,
∴点A在线段BC的垂直平分线上,
∴直线AD是线段BC的垂直平分线,
即AD⊥BC.
轴对称图形与等腰三角形》单元测试卷
一.选择题
1.现实世界中,对称现象无处不在.下列标志中,不是轴对称图形的是( )
A.
B.
C.
D.
2.如图,有A、B、C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.∠A、∠B两内角的平分线的交点处
B.AC、AB两边高线的交点处
C.AC、AB两边中线的交点处
D.AC、AB两边垂直平分线的交点处
3.已知△ABC的三边a,b,c满足(a﹣4)2++|c﹣4|=0,那么△ABC是( )
A.不等边三角形
B.等边三角形
C.等腰三角形
D.不能判断
4.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到长方形的边时反弹,反弹时反射角等于入射角(如:∠1=∠2,∠3=∠4).当小球第1次碰到长方形的边时的点为Q,第2次碰到长方形的边时的点为M…,第2019次碰到长方形的边时的点为图中的( )
A.N点
B.Q点
C.M点
D.P点
5.如图,保持△ABC的三个顶点的横坐标不变,纵坐标都乘﹣1,画出坐标变化后的三角形,则所得三角形与原三角形的关系是( )
A.关于x轴对称
B.关于y轴对称
C.将原图形沿x轴的负方向平移了1个单位
D.将原图形沿y轴的负方向平移了1个单位
6.剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A.
B.
C.
D.
7.已知等腰三角形的一边长为4cm,周长是18cm,则它的腰长是( )
A.4cm
B.7cm
C.10
cm
D.4cm或7cm
8.已知a,b,c是△ABC的三边长,且满足+|b﹣8|+(c﹣10)2=0,则△ABC是( )
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.以c为底边的等腰三角形
9.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
A.①②③④
B.①②③
C.②④
D.①③
10.如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=108°,则∠C的度数为( )
A.40°
B.41°
C.32°
D.36°
二.填空题
11.如图,在△ABC中,BC边的垂直平分线分别交AB、BC于D、E,BE=4,△ADC的周长为18,则△ABC的周长为
.
12.如图,在△ABC中,∠ABC=90°,∠A=60°,CD=CB,∠ABD=
.
13.已知∠AOB=30°且∠AOB内有一点P,点P关于OA、OB的对称点分别为E、F,则△EOF一定是
三角形.
14.如图,四边形ABCD中,∠BCD=90°,∠ABD=∠DBC,AB=4,DC=6,则△ABD的面积为
.
15.已知:如图,△ABC中,BO平分∠ABC,CO平分∠ACB交BO于点O,过点O作DE∥BC交AB于点D,交AC于点E,则△ADE的周长可用△ABC的边表示为
.
16.等腰三角形的周长为18cm,其中一边长为4cm,则该等腰三角形的底边长为
.
17.如图,在△ABC中,D是AC边的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,联结AC′.若AD=AC′=2,BD=3,则点D到BC′的距离为
.
18.如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且=,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为
.
19.如图1是个轴对称图形,且每个角都是直角,长度如图所示,小王按照如图2所示的方法玩拼图游戏,两两相扣,相互不留空隙,那么小王用2020个这样的图形(图1)拼出来的图形的总长度是
.(结果用m,n表示)
20.雨后,地上的积水犹如一块澄澈的平面镜,某路段监控摄像头在雨后拍摄,由于位置偏离,拍摄中心聚集在了水面上,摄像头侦测到一小轿车超速行驶,积水中倒映的车牌为“”,那么该小轿车的真实车牌号为
.
三.解答题
21.一个台球桌的桌面如图所示,一个球在桌面上的点A滚向桌边PQ,碰着PQ上的点B后便反弹而滚向桌边RS,碰着RS上的点C便反弹而滚向点D,如果PQ∥RS,AB、BC、CD都是直线,且∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,那么,球经过两次反弹后所滚的路径CD是否平行于原来的路径AB?
22.画图:试画出下列正多边形的所有对称轴,并完成表格,
正多边形的边数
3
4
5
6
7
…
对称轴的条数
…
根据上表,猜想正n边形有
条对称轴.
23.如图,在ΔABC中,∠C=90°,DE是AB的垂直平分线.
(1)若AC=5,BC=7,求ΔACD的周长;
(2)若∠BAD:∠CAD=2:1,求∠B的度数.
24.如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG=
;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=x°,过点C作CF∥OA交AB于点F,求∠BGO﹣∠ACF的度数.(用含x的代数式表示)
25.如图,在已知的平面直角坐标系中,AABC的顶点都在正方形网格的格点上,若点A、B、C的坐标分别是A(﹣2,1),B(﹣3,3),C(﹣1,4).
(1)画出△ABC关于x轴对称的图形△A1B1C1,并写出此时B1的坐标是:
.
(2)画出△ABC沿x轴正方向平移3个单位,再沿y轴负方向平移2个单位的图形△A2B2C2.
(3)△ABC的面积.
26.已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.求证:△OCD是等边三角形.
27.已知,如图,AB=AC,BO、CO分别是∠ABC和∠ACB的平分线,联结AO并延长交BC于点D,求证:AD⊥BC.
参考答案与试题解析
一.选择题
1.解:A、是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项符合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不合题意;
故选:B.
2.解:根据线段垂直平分线上的点到线段两个端点的距离相等,超市应建在AC、AB两边垂直平分线的交点处,
故选:D.
3.解:∵(a﹣4)2++|c﹣4|=0,
∴a﹣4=0,b﹣4=0,c﹣4=0,
∴a=b=c=4,
∴△ABC的形状是等边三角形,
故选:B.
4.解:如图所示,经过6次反弹后动点回到出发点P,
∵2019÷6=336…3,
∴当点P第2019次碰到矩形的边时为第337个循环组的第3次反弹,
∴第2019次碰到矩形的边时的点为图中的点N,
故选:A.
5.解:∵纵坐标乘以﹣1,
∴变化前后纵坐标互为相反数,
又∵横坐标不变,
∴所得三角形与原三角形关于x轴对称.
故选:A.
6.解:按照图中的顺序,向右对折,向上对折,从斜边处剪去一个直角三角形,从直角顶点处剪去一个等腰直角三角形,展开后实际是从原菱形的四边处各剪去一个直角三角形,从菱形的中心剪去一个正方形,可得:
.
故选:A.
7.解:分情况考虑:当4是腰时,则底边长是18﹣8=10,此时4,4,10不能组成三角形,应舍去;
当4是底边时,腰长是(18﹣4)×=7,
4,7,7能够组成三角形.此时腰长是7.
故选:B.
8.解:由题意得,a﹣6=0,b﹣8=0,c﹣10=0,
解得a=6,b=8,c=10,
∵62+82=100=102,
∴a2+b2=c2,
∴∠ACB=90°,
故选:C.
9.解:∵BE是AC边的中线,
∴AE=CE,
∵△ABE的面积=,△BCE的面积=AB,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=180°﹣∠BAC﹣∠ACF,∠AGF=∠DGC=180°﹣∠ADC﹣∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故④错误;
即正确的为①③,
故选:D.
10.解:如图所示,连接CO并延长,
设∠ACB=α,则∠A+∠B=180°﹣α,
由折叠可得,∠DOE=∠A,∠FOE=∠B,
∴∠DOF=∠A+∠B=180°﹣α,
∵∠DOG是△COD的外角,
∴∠DOG=∠DCO+∠CDO,
同理可得,∠FOG=∠FCO+∠CFO,
∴∠DOF=ACB+∠CDO+∠CFO,
即180°﹣α=α+108°,
解得α=36°,
∴∠ACB=36°,
故选:D.
二.填空题
11.解:∵DE是线段BC的垂直平分线,BE=4,
∴DB=DC,BC=2BE=8,
∵△ADC的周长为18,
∴AC+AD+DC=18,
∴AC+AD+DB=AC+AB=18,
∴△ABC的周长=AC+AB+BC=26,
故答案为:26.
12.解:∵∠ABC=90°,∠A=60°,
∴∠C=90°﹣∠A=90°﹣60°=30°,
∵CD=CB,
∴∠CBD=(180°﹣∠C)=(180°﹣30°)=75°,
∴∠ABD=∠ABC﹣∠CBD
=90°﹣75°
=15°.
故答案为:15°.
13.解:如图.连接OP,OE,OF.
∵点P关于OA的对称点为E,
∴OA是PE的垂直平分线,
∴OP=OE;
同理OF=OP,
∴OE=OF.
∴△EOF是等腰三角形.
∵∠AOB=30°,
∴∠EOF=60°,
∴等腰△EOF是等边三角形.
14.解:过D作DE⊥BA,交BA的延长线于E,
∵∠BCD=90°,∠ABD=∠DBC,
∴DE=DC,
∵DC=6,
∴DE=6,
∵AB=4,
∴△ABD的面积是==12,
故答案为:12.
15.解:∵BO平分∠ABC,CO平分∠ACB,
∴∠DBO=∠OBC,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠OBC,∠COE=∠OCB,
∴∠DOB=∠DBO,∠EOC=∠OCE,
∴BD=DO,OE=CE,
∴△ADE的周长=AD+DO+OE+AE=AD+DB+AE+EC=AB+AC
故答案为:AB+AC.
16.解:当4cm为底边长时,腰长为(18﹣4)÷2=7(cm),
当4cm为腰长时,底边长为18﹣4×2=10(cm),
∵4+4<10,
∴当4cm为腰长时,不能组成三角形,
∴该等腰三角形的底边长为4cm,
故答案为4cm.
17.解:如图,连接CC',交BD于点M,过点D作DH⊥BC'于点H,
∵AD=AC′=2,D是AC边上的中点,
∴DC=AD=2,
由翻折知,△BDC≌△BDC',BD垂直平分CC',
∴DC=DC'=2,BC=BC',CM=C'M,
∴AD=AC′=DC'=2,
∴△ADC'为等边三角形,
∴∠ADC'=∠AC'D=∠C'AC=60°,
∵DC=DC',
∴∠DCC'=∠DC'C=×60°=30°,
在Rt△C'DM中,
∠DC'C=30°,DC'=2,
∴DM=1,C'M=DM=,
∴BM=BD﹣DM=3﹣1=2,
在Rt△BMC'中,
BC'===,
∵S△BDC'=BC'?DH=BD?CM,
∴DH=3×,
∴DH=,
∵∠DCB=∠DBC',
∴点D到BC的距离为.
故答案为:.
18.解:∵在Rt△ABO中,∠OBA=90°,A(4,4),
∴AB=OB=4,∠AOB=45°,
∵=,点D为OB的中点,
∴BC=3,OD=BD=2,
∴D(2,0),C(4,3),
作D关于直线OA的对称点E,连接EC交OA于P,
则此时,四边形PDBC周长最小,E(0,2),
∵直线OA
的解析式为y=x,
设直线EC的解析式为y=kx+b,
∴,
解得:,
∴直线EC的解析式为y=x+2,
解得,,
∴P(,),
故答案为:(,).
19.解:由图可得,2个这样的图形(图1)拼出来的图形中,重叠部分的长度为m﹣n,
∴用2020个这样的图形(图1)拼出来的图形的总长度=2020m﹣2019(m﹣n)=m+2019n,
故答案为:m+2019n.
20.解:利用轴对称的性质得出:
该汽车牌照号码为:苏N?2020N.
故答案为:苏N?2020N.
三.解答题
21.解:球经过两次反弹后所滚的路径CD平行于原来的路径AB.理由如下:
∵PQ∥RS,∠ABC的平分线BN垂直于PQ,∠BCD的平分线CM垂直于RS,
∴BN∥CM,
∴∠CBN=∠BCM,
又∵∠ABC=2∠CBN,∠BCD=2∠BCM,
∴∠ABC=∠BCD,
∴CD∥AB.
22.解:如图,
故填3,4,5,6,7,n.
23.解:(1)∵DE是AB的垂直平分线,
∴DA=DB,
∴ΔACD的周长=AC+CD+DA=AC+CD+DB+AC+CB=5+7=12;
(2)∵DA=DB,
∴∠BAD=∠B,
设∠CAD=x,则∠BAD=∠B=2x,
∵∠C=90°,
∴∠CAB+∠B=90°,即x+2x+2x=90°,
解得,x=18°,
∴∠B=2x=36°.
24.解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°﹣n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°﹣n°,
∴∠ACG=∠CBA+∠CAB=90°﹣n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO﹣∠ACF=∠BGO﹣∠CAG=∠ACG=90°﹣x°.
25.解:(1)如图所示,△A1B1C1即为所求,此时B1的坐标是(﹣3,﹣3),
故答案为:(﹣3,﹣3).
(2)如图所示,△A2B2C2即为所求,
(3)△ABC的面积为2×3﹣×1×3﹣×1×2﹣1×2=2.5.
26.证明:∵△ABO是等边三角形,
∴∠A=∠B=∠AOB=60°,
∵AB∥CD,
∴∠C=∠A=60°,∠D=∠B=60°,
∴∠COD=∠AOB=60°,
∴△OCD是等边三角形.
27.证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BO、CO分别是∠ABC和∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=ACB,
∴∠OBC=∠OCB,
∴OB=OC,
∴点O在线段BC的垂直平分线上,
∵AB=AC,
∴点A在线段BC的垂直平分线上,
∴直线AD是线段BC的垂直平分线,
即AD⊥BC.
