2020-2021学年北师大版九年级数学下册第三章《圆》达标测试卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册第三章《圆》达标测试卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 21:59:08 | ||
图片预览




文档简介
第三章达标测试卷
一、选择题(每题3分,共30分)
1.⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5
B.6
C.7
D.8
2.如图,在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径为( )
A.5
B.10
C.8
D.6
3.如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则tan∠BAC的值是( )
A.
B.1
C.
D.
4.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD等于( )
A.128°
B.100°
C.64°
D.32°
5.已知扇形的面积为4π,扇形的弧长为π,则该扇形的半径为( )
A.4
B.6
C.8
D.8π
6.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是( )
A.1
B.2
C.
D.
7.如图,AB是⊙O的直径,CD是⊙O的弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠A=∠D
B.=
C.∠ACB=90°
D.∠COB=3∠D
8.同一个圆的内接正六边形和外切正六边形的周长之比为( )
A.3∶4
B.∶2
C.2∶
D.1∶2
9.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
A.10
B.8
C.4
D.2
10.如图,已知⊙O是等腰直角三角形ABC的外接圆,点D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( )
A.3
B.2
C.1
D.1.2
二、填空题(每题3分,共30分)
11.如图,在⊙O中,=,∠A=40°,则∠B=________.
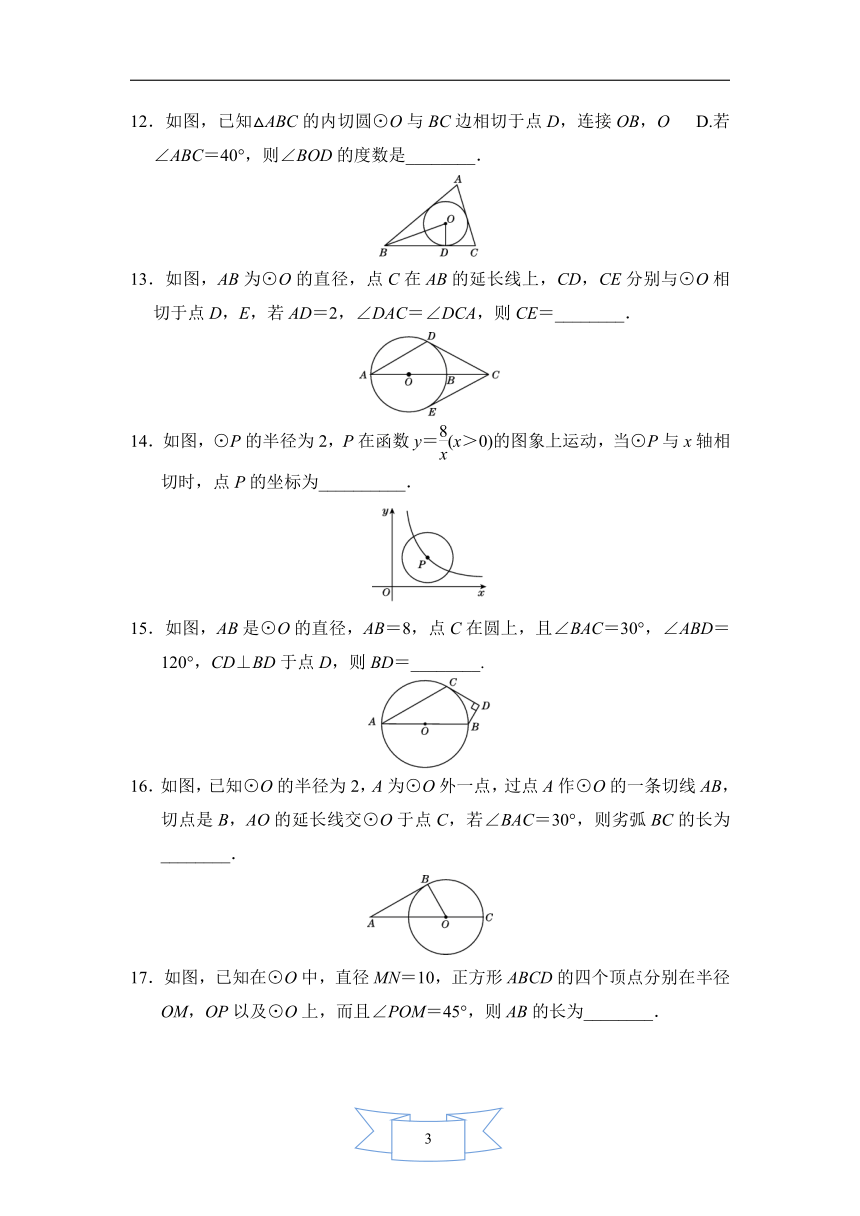
12.如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,O
D.若∠ABC=40°,则∠BOD的度数是________.
13.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E,若AD=2,∠DAC=∠DCA,则CE=________.
14.如图,⊙P的半径为2,P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,点P的坐标为__________.
15.如图,AB是⊙O的直径,AB=8,点C在圆上,且∠BAC=30°,∠ABD=120°,CD⊥BD于点D,则BD=________.
16.如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧BC的长为________.
17.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM,OP以及⊙O上,而且∠POM=45°,则AB的长为________.
18.如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=________.
19.如图,直线y=x+与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P有________个.
20.如图,在Rt△ABC中,∠ACB=90°,AC=2,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为__________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.如图,A,B,C三点都在⊙O上,AE是⊙O的直径,AD是△ABC的高,⊙O的半径R=4,AD=6.
求证:AB·AC的值是一个常数.
22.如图,⊙O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
(2)延长ED到点P,过P作⊙O的切线,切点为C,若PC=2,求PD的长.
23.如图,已知P为反比例函数y=(x>0)图象上一点,以点P为圆心,OP长为半径画圆,⊙P与x轴相交于点A,连接PA,且点A的坐标为(4,0).求:
(1)⊙P的半径;
(2)图中阴影部分的面积.
24.如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
25.如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线对应的函数表达式.
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
26.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB,BC于点M,N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2,sin
∠BCP=,求点B到AC的距离;
(3)在(2)的条件下,求△ACP的周长.
答案
一、1.A 2.A 3.D 4.A 5.C 6.A
7.D 8.B
9.D 点拨:连接BM,OM,AM,过点M作MH⊥BC于点H.
∵⊙M与x轴相切于点A(8,0),
∴AM⊥OA,OA=8.∴∠OAM=∠MHO=∠HOA=90°.
∴四边形OAMH是矩形,∴AM=OH.
∵点B的坐标为(0,4),点C的坐标为(0,16),
∴OB=4,OC=16.∴BC=12.
∵MH⊥BC,∴CH=BH=BC=×12=6.
∴OH=OB+BH=4+6=10.
∴AM=10.
在Rt△AOM中,OM===2.
10.C 点拨:∵⊙O是等腰直角三角形ABC的外接圆,BC=4,∴AB为⊙O的直径,AC=4,AB=4.
∴∠D=90°.
在Rt△ABD中,AD=,AB=4,∴BD=.
∵∠D=∠C,∠DAE=∠CBE,∴△ADE∽△BCE.
∴AD∶BC=AE∶BE=DE∶CE=∶4=1∶5.∴相似比为1∶5.
设AE=x,∴BE=5x.∴DE=-5x.∴CE=5DE=28-25x.
又∵AC=4,∴x+28-25x=4.解得x=1.
二、11.70° 12.70° 13.2 14.(4,2)
15.2 16. 17.
18.
点拨:延长CO与圆交于点D,连接AD,可得∠B=∠D,故sin
B=sin
D.∴=,即=,可得AB=.
19.3
20.2- 点拨:依题意,有AD=BD,BC=DC.因为∠ACB=90°,所以CB=CD=BD,即△BCD为等边三角形,所以∠BCD=∠ABC=60°.又因为AD=DC,所以∠BAC=∠ACD=30°.由AC=2,得BC=2,AB=4.阴影部分的面积为S△ACD-S弓形AD=S△ACD-S弓形BD=S△ACD-(S扇形BCD-S△BCD)=S△ABC-S扇形BCD,根据面积公式计算即可.
三、21.证明:连接BE,如图所示.
∵AE为⊙O的直径,AD是△ABC的高,
∴∠ABE=∠ADC=90°.
又∵∠C=∠E,∴△ADC∽△ABE.
∴=.
∴AB·AC=AD·AE=6×2R=6×2×4=48,即AB·AC的值是一个常数.
22.解:(1)连接OD.
∵AB=10,∴OA=OD=5.∵AH=2,∴OH=3.
∵AB⊥DE,∴∠DHO=90°,DH=EH.
∴DH===4.
∴DE=2DH=2×4=8.
(2)连接OC,OP.
∵CP与⊙O相切,∴OC⊥CP.
∴OP===3.
∴PH===6.
∴PD=PH-DH=6-4=2.
23.解:(1)过点P作PD⊥x轴于点D.
∵A点的坐标为(4,0),∴OA=4.
∴OD=2,即点P的横坐标为2.
将x=2代入y=,可得y=2,即PD=2.
在Rt△OPD中,根据勾股定理可得OP=2,即⊙P的半径为2.
(2)由(1)可得PD=OD,且∠ODP=90°,∴∠OPD=45°.
又∵OP=PA,
∴∠APD=∠OPD=45°.
∴∠OPA=90°.
又∵OA=4,PD=2,
∴S阴影=S扇形OPA-S△OPA=-=2π-4.
24.(1)证明:连接OD,OE,BD.
∵AB为半圆O的直径,
∴∠ADB=∠BDC=90°.
在Rt△BDC中,E为斜边BC的中点,∴DE=BE.
在△OBE和△ODE中,
∴△OBE≌△ODE(SSS).
∴∠ODE=∠OBE=90°.∴DE为半圆O的切线.
(2)解:在Rt△ABC中,∠BAC=30°,∴BC=AC.
∵BC=2BE=2DE=4,∴AC=8.
易知∠C=60°,DE=EC,
∴△DEC为等边三角形.
∴DC=DE=2.
∴AD=AC-DC=8-2=6.
25.解:(1)设经过B,C两点的直线对应的函数表达式为y=mx+n(m≠0且m,n为常数).
分别将B(0,3),C(1,0)的坐标代入y=mx+n,得解得
∴经过B,C两点的直线对应的函数表达式为y=-3x+3.
(2)直线BC与⊙O′有3种位置关系:相切、相交、相离.当BC切⊙O′于第二象限时,记切点为D,易得DC=.
∵BO=BD=b,∴BC=-b.
在Rt△OBC中,易得12+b2=(-b)2,解得b=.
同理当BC切⊙O′于第三象限时,可求得b=-.
故当b>或b<-时,直线BC与⊙O′相离;
当b=或-时,直线BC与⊙O′相切;
当-<b<时,直线BC与⊙O′相交.
26.(1)证明:如图,连接AN.
∵∠ABC=∠ACB,∴AB=AC.
∵AC为直径,∴AN⊥BC.
∴∠CAN=∠BAN,BN=CN.
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
即∠ACP=90°.
∴直线CP是⊙O的切线.
(2)解:如图,过点B作BH⊥AC于点H,由(1)得BN=CN=BC=.
∵AN⊥BC,∴sin∠CAN=.
又∵∠CAN=∠BCP,sin
∠BCP=,
∴=,∴AC=5.
∴AN==2.
∵∠ANC=∠BHC=90°,∠ACN=∠BCH,
∴△CAN∽△CBH.∴=.
∴BH=4,即点B到AC的距离为4.
(3)解:易知CH==2,
则AH=AC-CH=3.
易知△ABH∽△APC,∴=.
∴PC=.
∴AP==.
∴△ACP的周长是AC+AP+PC=5++=20.
一、选择题(每题3分,共30分)
1.⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5
B.6
C.7
D.8
2.如图,在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径为( )
A.5
B.10
C.8
D.6
3.如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则tan∠BAC的值是( )
A.
B.1
C.
D.
4.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD等于( )
A.128°
B.100°
C.64°
D.32°
5.已知扇形的面积为4π,扇形的弧长为π,则该扇形的半径为( )
A.4
B.6
C.8
D.8π
6.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则⊙O的半径是( )
A.1
B.2
C.
D.
7.如图,AB是⊙O的直径,CD是⊙O的弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠A=∠D
B.=
C.∠ACB=90°
D.∠COB=3∠D
8.同一个圆的内接正六边形和外切正六边形的周长之比为( )
A.3∶4
B.∶2
C.2∶
D.1∶2
9.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
A.10
B.8
C.4
D.2
10.如图,已知⊙O是等腰直角三角形ABC的外接圆,点D是上一点,BD交AC于点E,若BC=4,AD=,则AE的长是( )
A.3
B.2
C.1
D.1.2
二、填空题(每题3分,共30分)
11.如图,在⊙O中,=,∠A=40°,则∠B=________.
12.如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,O
D.若∠ABC=40°,则∠BOD的度数是________.
13.如图,AB为⊙O的直径,点C在AB的延长线上,CD,CE分别与⊙O相切于点D,E,若AD=2,∠DAC=∠DCA,则CE=________.
14.如图,⊙P的半径为2,P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,点P的坐标为__________.
15.如图,AB是⊙O的直径,AB=8,点C在圆上,且∠BAC=30°,∠ABD=120°,CD⊥BD于点D,则BD=________.
16.如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧BC的长为________.
17.如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM,OP以及⊙O上,而且∠POM=45°,则AB的长为________.
18.如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB=________.
19.如图,直线y=x+与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O,若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P有________个.
20.如图,在Rt△ABC中,∠ACB=90°,AC=2,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为__________.
三、解答题(21题8分,26题12分,其余每题10分,共60分)
21.如图,A,B,C三点都在⊙O上,AE是⊙O的直径,AD是△ABC的高,⊙O的半径R=4,AD=6.
求证:AB·AC的值是一个常数.
22.如图,⊙O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
(2)延长ED到点P,过P作⊙O的切线,切点为C,若PC=2,求PD的长.
23.如图,已知P为反比例函数y=(x>0)图象上一点,以点P为圆心,OP长为半径画圆,⊙P与x轴相交于点A,连接PA,且点A的坐标为(4,0).求:
(1)⊙P的半径;
(2)图中阴影部分的面积.
24.如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
25.如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线对应的函数表达式.
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
26.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB,BC于点M,N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2,sin
∠BCP=,求点B到AC的距离;
(3)在(2)的条件下,求△ACP的周长.
答案
一、1.A 2.A 3.D 4.A 5.C 6.A
7.D 8.B
9.D 点拨:连接BM,OM,AM,过点M作MH⊥BC于点H.
∵⊙M与x轴相切于点A(8,0),
∴AM⊥OA,OA=8.∴∠OAM=∠MHO=∠HOA=90°.
∴四边形OAMH是矩形,∴AM=OH.
∵点B的坐标为(0,4),点C的坐标为(0,16),
∴OB=4,OC=16.∴BC=12.
∵MH⊥BC,∴CH=BH=BC=×12=6.
∴OH=OB+BH=4+6=10.
∴AM=10.
在Rt△AOM中,OM===2.
10.C 点拨:∵⊙O是等腰直角三角形ABC的外接圆,BC=4,∴AB为⊙O的直径,AC=4,AB=4.
∴∠D=90°.
在Rt△ABD中,AD=,AB=4,∴BD=.
∵∠D=∠C,∠DAE=∠CBE,∴△ADE∽△BCE.
∴AD∶BC=AE∶BE=DE∶CE=∶4=1∶5.∴相似比为1∶5.
设AE=x,∴BE=5x.∴DE=-5x.∴CE=5DE=28-25x.
又∵AC=4,∴x+28-25x=4.解得x=1.
二、11.70° 12.70° 13.2 14.(4,2)
15.2 16. 17.
18.
点拨:延长CO与圆交于点D,连接AD,可得∠B=∠D,故sin
B=sin
D.∴=,即=,可得AB=.
19.3
20.2- 点拨:依题意,有AD=BD,BC=DC.因为∠ACB=90°,所以CB=CD=BD,即△BCD为等边三角形,所以∠BCD=∠ABC=60°.又因为AD=DC,所以∠BAC=∠ACD=30°.由AC=2,得BC=2,AB=4.阴影部分的面积为S△ACD-S弓形AD=S△ACD-S弓形BD=S△ACD-(S扇形BCD-S△BCD)=S△ABC-S扇形BCD,根据面积公式计算即可.
三、21.证明:连接BE,如图所示.
∵AE为⊙O的直径,AD是△ABC的高,
∴∠ABE=∠ADC=90°.
又∵∠C=∠E,∴△ADC∽△ABE.
∴=.
∴AB·AC=AD·AE=6×2R=6×2×4=48,即AB·AC的值是一个常数.
22.解:(1)连接OD.
∵AB=10,∴OA=OD=5.∵AH=2,∴OH=3.
∵AB⊥DE,∴∠DHO=90°,DH=EH.
∴DH===4.
∴DE=2DH=2×4=8.
(2)连接OC,OP.
∵CP与⊙O相切,∴OC⊥CP.
∴OP===3.
∴PH===6.
∴PD=PH-DH=6-4=2.
23.解:(1)过点P作PD⊥x轴于点D.
∵A点的坐标为(4,0),∴OA=4.
∴OD=2,即点P的横坐标为2.
将x=2代入y=,可得y=2,即PD=2.
在Rt△OPD中,根据勾股定理可得OP=2,即⊙P的半径为2.
(2)由(1)可得PD=OD,且∠ODP=90°,∴∠OPD=45°.
又∵OP=PA,
∴∠APD=∠OPD=45°.
∴∠OPA=90°.
又∵OA=4,PD=2,
∴S阴影=S扇形OPA-S△OPA=-=2π-4.
24.(1)证明:连接OD,OE,BD.
∵AB为半圆O的直径,
∴∠ADB=∠BDC=90°.
在Rt△BDC中,E为斜边BC的中点,∴DE=BE.
在△OBE和△ODE中,
∴△OBE≌△ODE(SSS).
∴∠ODE=∠OBE=90°.∴DE为半圆O的切线.
(2)解:在Rt△ABC中,∠BAC=30°,∴BC=AC.
∵BC=2BE=2DE=4,∴AC=8.
易知∠C=60°,DE=EC,
∴△DEC为等边三角形.
∴DC=DE=2.
∴AD=AC-DC=8-2=6.
25.解:(1)设经过B,C两点的直线对应的函数表达式为y=mx+n(m≠0且m,n为常数).
分别将B(0,3),C(1,0)的坐标代入y=mx+n,得解得
∴经过B,C两点的直线对应的函数表达式为y=-3x+3.
(2)直线BC与⊙O′有3种位置关系:相切、相交、相离.当BC切⊙O′于第二象限时,记切点为D,易得DC=.
∵BO=BD=b,∴BC=-b.
在Rt△OBC中,易得12+b2=(-b)2,解得b=.
同理当BC切⊙O′于第三象限时,可求得b=-.
故当b>或b<-时,直线BC与⊙O′相离;
当b=或-时,直线BC与⊙O′相切;
当-<b<时,直线BC与⊙O′相交.
26.(1)证明:如图,连接AN.
∵∠ABC=∠ACB,∴AB=AC.
∵AC为直径,∴AN⊥BC.
∴∠CAN=∠BAN,BN=CN.
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
即∠ACP=90°.
∴直线CP是⊙O的切线.
(2)解:如图,过点B作BH⊥AC于点H,由(1)得BN=CN=BC=.
∵AN⊥BC,∴sin∠CAN=.
又∵∠CAN=∠BCP,sin
∠BCP=,
∴=,∴AC=5.
∴AN==2.
∵∠ANC=∠BHC=90°,∠ACN=∠BCH,
∴△CAN∽△CBH.∴=.
∴BH=4,即点B到AC的距离为4.
(3)解:易知CH==2,
则AH=AC-CH=3.
易知△ABH∽△APC,∴=.
∴PC=.
∴AP==.
∴△ACP的周长是AC+AP+PC=5++=20.
