人教版 数学八年级上册课件 14.1.3 积的乘方(16张)
文档属性
| 名称 | 人教版 数学八年级上册课件 14.1.3 积的乘方(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
14.1.3
积的乘方
回顾
&
思考
?
?
?
幂的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an
=
?
am+n
(m、n都是正整数)
幂的乘方运算法则:
?
(am)n=
(m、n都是正整数)
amn
填空:
1.
am+am=_____.
2.
a3·a5=_______.
3.
若am=8,an=30,则am+n=____.
4.
(a4)3=____.
(m4)2+m5·m3=____,
(a3)5·(a2)2=____.
2am
a8
240
a12
2m8
a19
创设情境
在手工课上,小明制作了一个正方体的模具,其棱长是
,问该模具的体积是多少?
解:(4×102)3
探究:
计算
(3×4)2与32
×
42,你会发现什么?
122
144
9×16
144
=
∵
(3×4)2=
=
32
×42=
=
∴
(3×4)2
32
×
42
结论:(3×4)2与32
×
42相等
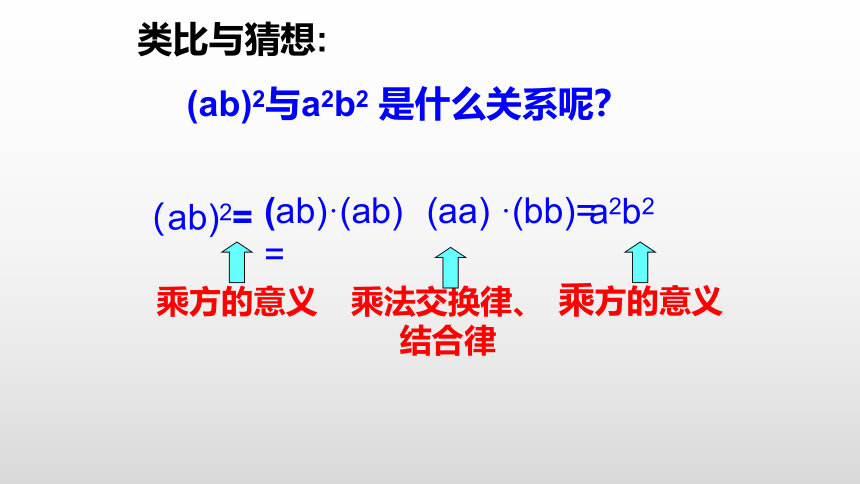
类比与猜想:
(ab)2与a2b2
是什么关系呢?
(ab)2=
(ab)·(ab)=
(aa)
·(bb)=
a2b2
乘方的意义
乘方的意义
乘法交换律、结合律
猜想:
(ab)n
=
(当m、n都是正整数)
即:
(乘方的意义)
(乘法结合律)
(乘方的意义)
an·bn
(ab)n
=
ab·ab·……·ab
=(a·a·……·a)
(b·b·……·b)
=an·bn
n个ab
n个a
n个b
(ab)n
=
(当m、n都是正整数)
an·bn
积的乘方法则:
(ab)n
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
=
anbn(n为正整数)
积的乘方
乘方的积
(abc)n
=
anbncn(n为正整数)
推广:三个或三个以上的积的乘方等于什么?
练习(1)(ab3)2
=
ab6
×
×
(ab3)2
=
a2b6
(2)(-a2b3)5
=
a10b15
(-a2b3)5
=
-a10b15
(3)(3a3b2)
3
=
9a9b6
×
(3a3b2)
3
=
27a9b6
计算:
(1)(-2x2y3)3
(2)
(-3a3b2c)4
例1:
解:(1)原式=(-2)3
·(x2)3
·(y3)3
(2)原式=(-3)4
·(a3)4
·(b2)4
·
c4
=-8x6y9
=
81
a12b8c4
(1)负数乘方的符号法则。
(2)积的乘方等于积中“每一个”因式乘方的积,防止有的因式漏乘方错误。
想一想,我们在计算时应注意什么?
练1
计算:
公式的反向使用
(ab)n
=
an·bn
(m,n都是正整数)
反向使用:
an·bn
=
(ab)n
试用简便方法计算:
(1)
23×53
(2)
28×58
=
(2×5)3
=
103
=
(2×5)8
=
108
(3)
(-5)16
×
(-2)15
(4)
24
×
44
×(-0.125)4
=
(-5)×[(-5)×(-2)]15
=
-5×1015
=
[2×4×(-0.125)]4
=
14
=
1
.
小结:
1、本节课的主要内容:
am·an=am+n
(am)n=amn
(ab)n=anbn
(
m、n都是正整数)
2、
运用积的乘方法则时要注意什么?
公式中的a、b代表任何代数式;每一个因式
都要“乘方”;注意结果的符号、幂指数及其逆向运用。(混合运算要注意运算顺序)
积的乘方
幂的运算的三条重要性质:
课堂小测
下面的计算对不对?如果不对,应该怎样改正?
(
)
(
)
(
)
(
)
(
)
不是积的乘方运算
拓展提高
积的乘方
(ab)n=anbn
14.1.3
积的乘方
回顾
&
思考
?
?
?
幂的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an
=
?
am+n
(m、n都是正整数)
幂的乘方运算法则:
?
(am)n=
(m、n都是正整数)
amn
填空:
1.
am+am=_____.
2.
a3·a5=_______.
3.
若am=8,an=30,则am+n=____.
4.
(a4)3=____.
(m4)2+m5·m3=____,
(a3)5·(a2)2=____.
2am
a8
240
a12
2m8
a19
创设情境
在手工课上,小明制作了一个正方体的模具,其棱长是
,问该模具的体积是多少?
解:(4×102)3
探究:
计算
(3×4)2与32
×
42,你会发现什么?
122
144
9×16
144
=
∵
(3×4)2=
=
32
×42=
=
∴
(3×4)2
32
×
42
结论:(3×4)2与32
×
42相等
类比与猜想:
(ab)2与a2b2
是什么关系呢?
(ab)2=
(ab)·(ab)=
(aa)
·(bb)=
a2b2
乘方的意义
乘方的意义
乘法交换律、结合律
猜想:
(ab)n
=
(当m、n都是正整数)
即:
(乘方的意义)
(乘法结合律)
(乘方的意义)
an·bn
(ab)n
=
ab·ab·……·ab
=(a·a·……·a)
(b·b·……·b)
=an·bn
n个ab
n个a
n个b
(ab)n
=
(当m、n都是正整数)
an·bn
积的乘方法则:
(ab)n
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
=
anbn(n为正整数)
积的乘方
乘方的积
(abc)n
=
anbncn(n为正整数)
推广:三个或三个以上的积的乘方等于什么?
练习(1)(ab3)2
=
ab6
×
×
(ab3)2
=
a2b6
(2)(-a2b3)5
=
a10b15
(-a2b3)5
=
-a10b15
(3)(3a3b2)
3
=
9a9b6
×
(3a3b2)
3
=
27a9b6
计算:
(1)(-2x2y3)3
(2)
(-3a3b2c)4
例1:
解:(1)原式=(-2)3
·(x2)3
·(y3)3
(2)原式=(-3)4
·(a3)4
·(b2)4
·
c4
=-8x6y9
=
81
a12b8c4
(1)负数乘方的符号法则。
(2)积的乘方等于积中“每一个”因式乘方的积,防止有的因式漏乘方错误。
想一想,我们在计算时应注意什么?
练1
计算:
公式的反向使用
(ab)n
=
an·bn
(m,n都是正整数)
反向使用:
an·bn
=
(ab)n
试用简便方法计算:
(1)
23×53
(2)
28×58
=
(2×5)3
=
103
=
(2×5)8
=
108
(3)
(-5)16
×
(-2)15
(4)
24
×
44
×(-0.125)4
=
(-5)×[(-5)×(-2)]15
=
-5×1015
=
[2×4×(-0.125)]4
=
14
=
1
.
小结:
1、本节课的主要内容:
am·an=am+n
(am)n=amn
(ab)n=anbn
(
m、n都是正整数)
2、
运用积的乘方法则时要注意什么?
公式中的a、b代表任何代数式;每一个因式
都要“乘方”;注意结果的符号、幂指数及其逆向运用。(混合运算要注意运算顺序)
积的乘方
幂的运算的三条重要性质:
课堂小测
下面的计算对不对?如果不对,应该怎样改正?
(
)
(
)
(
)
(
)
(
)
不是积的乘方运算
拓展提高
积的乘方
(ab)n=anbn
