2020-2021学年沪科新版七年级上册数学《第3章 一次方程与方程组》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年沪科新版七年级上册数学《第3章 一次方程与方程组》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 23:36:38 | ||
图片预览



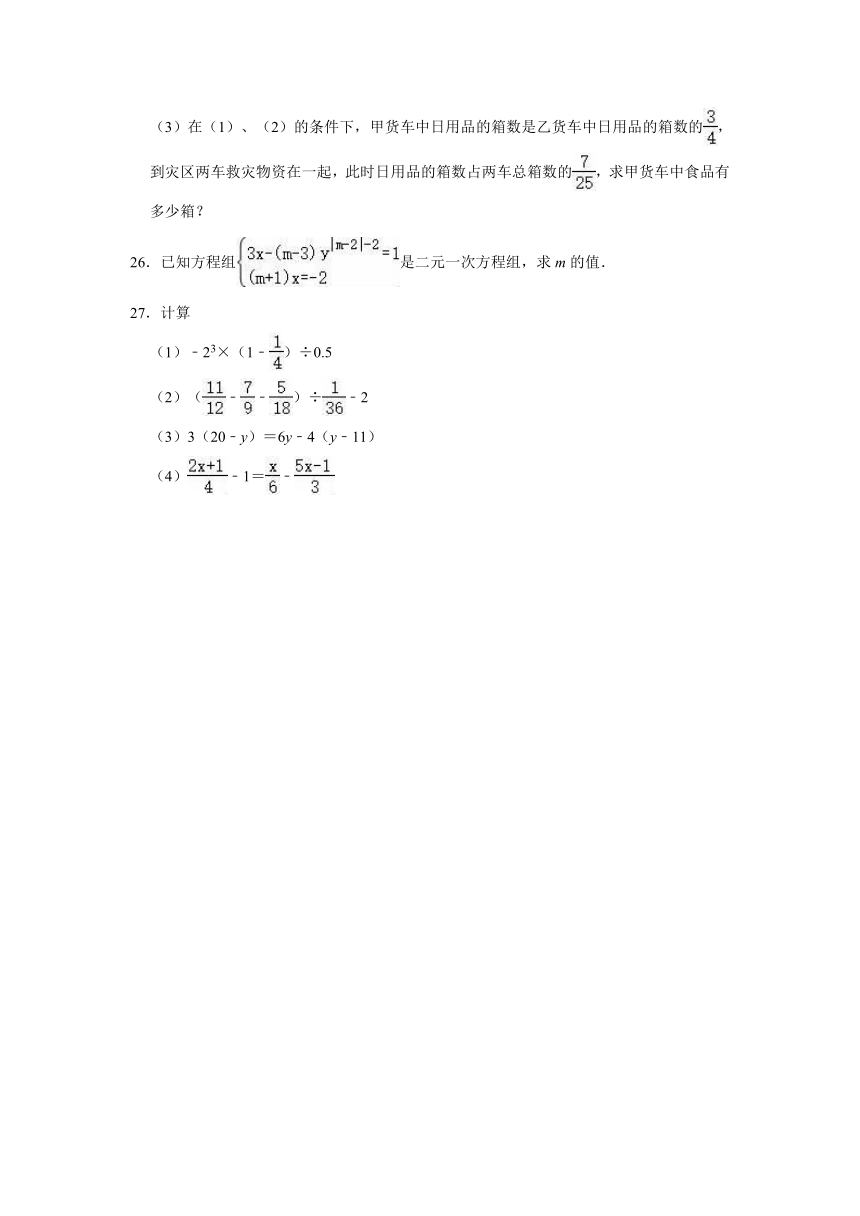

文档简介
2020-2021学年沪科新版七年级上册数学《第3章
一次方程与方程组》单元测试卷
一.选择题
1.下列各式中,是方程的是( )
A.
B.14﹣5=9
C.a>3b
D.x=1
2.下列方程中,是二元一次方程的是( )
A.xy=2
B.3x=4y
C.x+=2
D.x2+2y=4
3.根据等式的性质,下列选项中等式不一定成立的是( )
A.若a=b,则a+2=b+2
B.若ax=bx,则a=b
C.若=,则x=y
D.若3a=3b,则a=b
4.方程x+y=4与2x﹣3y=3的公共解是( )
A.
B.
C.
D.
5.若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为
( )
A.
B.
C.
D.
6.陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定弄错了.”陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,那么笔记本的单价可能是( )元.
A.1元
B.2元
C.3元
D.4元
7.某理财产品的年收益率为5.21%,若张老师购买x万元该种理财产品,定期2年,则2年后连同本金共有10万元,则根据题意列方程正确的是( )
A.(1+5.21)x=10
B.(1+5.21)2x=10
C.(1+5.21%)x=10
D.(1+5.21%)2x=10
8.解方程组得x等于( )
A.18
B.11
C.10
D.9
9.若整数a使关于x的方程ax+3=﹣9﹣x有负整数解,且a也是四条直线在平面内交点的个数,则满足条件的所有a的个数为( )
A.3
B.4
C.5
D.6
10.已知方程|x|=ax+1有一个负根而且没有正根,那么a的取值范围是( )
A.a>﹣1
B.a=1
C.a≥1
D.非上述答案
二.填空题
11.把三元一次方程组化为二元一次方程组
.
12.一支部队第一天行军4小时,第二天行军5小时,两天共行军196千米,如果设第一天每小时行军x千米,第二天每小时行军y千米,依题意,可列方程为
.
13.有A、B、C三种商品,如果购5件A、2件B、3件C共需513元,购3件A、6件B、5件C共需375元,那么购A、B、C各一件共需
元.
14.一个数的是,那么这个数是
.
15.若|x+y﹣5|+(x﹣y+3)2=0,则x2﹣y2=
.
16.一个两位数的十位数字与个位数字的和是13,把这个两位数减去27,结果恰好成为数字对调后组成的两位数,则这个两位数为
.
17.若2x﹣3与1互为相反数,则x=
.
18.如果是方程2x﹣3ay=16的一组解,则a=
.
19.2020年春节前夕“新型冠状病毒”爆发,某乡镇急需值班帐篷.某企业急灾区之所急,准备捐助甲、乙两种型号的帐篷2000顶,其中甲种帐篷每顶可安置6人,乙种帐篷每顶可安置4人,该企业捐助的帐篷共可安置9000人,设该企业捐助甲种帐篷x顶、乙种帐篷y顶,可列出的方程组为
.
20.2020年,受到新冠疫情的影响,全国市民都会佩戴口罩和配备一些消毒物品出门.某工厂生产的一种消毒套装深受市民喜爱,已知该消毒套装一套包含有2瓶消毒液,4包消毒湿巾,6个医用口罩,某医用超市向该厂订购了一批消毒套装,需要厂家在15天内生产完该套装并交货.该工厂将员工分为A、B、C三个组,分别对应生产消毒液、消毒湿巾、医用口罩;他们于某天零点开始工作,每天24小时轮班连续工作(假设每小时工作效率相同),若干天后的零点A组完成任务,再过几天后(不少于一天)的中午12点B组完成任务,再过几天(不少于一天)后的6时C组完成任务.已知A、B、C三个组每天完成的任务数分别是1080瓶,1440包,1440个,则该医用超市一共订购了
件消毒套装.
三.解答题
21.已知m满足,且满足|x+y﹣2020|=﹣|2020﹣x﹣y|,求m的值.
22.一个数减去它的,再加上等于,求这个数.
23.下表给出了代数式ax2+bx+c与x的一些对应值:
x
…
0
1
2
3
4
…
ax2+bx+c
…
3
m
﹣1
0
n
…
(1)利用表中所给数值求出a,b,c的值;
(2)直接写出:m=
,n=
;
(3)设y=ax2+bx+c,则当x取何值时,y<0.
24.某景点的门票价格如下表:
购票人数(人)
1~50
51~99
100以上(含100)
门票单价(元)
48
45
42
(1)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
25.哈美加在疫情期间决定往灾区捐赠物资,租用了甲和乙两种型号的货车,将已经装箱的药品、食品、日用品运往灾区,每辆车中均装有药品、食品、日用品,其中甲货车总共装箱400箱,药品的箱数占甲车总箱数的.
(1)甲货车中药品多少箱?
(2)若乙货车的总箱数比甲货车的总箱数多,且乙货车中食品箱数占乙货车总箱数的一半,求乙货车中食品有多少箱?
(3)在(1)、(2)的条件下,甲货车中日用品的箱数是乙货车中日用品的箱数的,到灾区两车救灾物资在一起,此时日用品的箱数占两车总箱数的,求甲货车中食品有多少箱?
26.已知方程组是二元一次方程组,求m的值.
27.计算
(1)﹣23×(1﹣)÷0.5
(2)(﹣﹣)÷﹣2
(3)3(20﹣y)=6y﹣4(y﹣11)
(4)﹣1=﹣
参考答案与试题解析
一.选择题
1.解:A、没有等号,故不是方程,故此选项错误;
B、等式中没有未知数,不是方程,故此选项错误;
C、是不等式,不是方程,故此选项错误;
D、符合方程的定义,是方程,故此选项正确;
故选:D.
2.解:A、是二元二次方程,故本选项不符合题意;
B、是二元一次方程,故本选项符合题意;
C、不是整式方程,故本选项不符合题意;
D、是二元二次方程,故本选项不符合题意;
故选:B.
3.解:∵若a=b,则a+2=b+2,
∴选项A不符合题意;
∵若ax=bx,则x=0时,a可以不等于b,
∴选项B符合题意;
∵若=,则x=y,
∴选项C不符合题意;
∵若3a=3b,则a=b,
∴选项D不符合题意.
故选:B.
4.解:联立得:,
①×3+②得:5x=15,
解得:x=3,
把x=3代入①得:y=1,
则方程组的解为.
故选:B.
5.解:,
①+②,得2x=10k.
∴x=5k.
①﹣②,得2y=﹣4k,
∴y=﹣2k.
∵二元一次方程组的解也是二元一次方程2x+3y=6的解,
∴2×5k+3×(﹣2k)=6.
即4k=6,
∴k=.
故选:B.
6.解:设购买单价为8元的书x本,笔记本的单价为y元,则购买单价为12元的书(105﹣x)本,
依题意,得:8x+y+12(105﹣x)=1500﹣418,
∴y=178﹣4x,
又∵x,y均为正整数,且y<5,
∴x=44,y=2.
故选:B.
7.解:设张老师购买x万元该种理财产品,
可得:(1+5.21%)2x=10,
故选:D.
8.解:,
①×2﹣②得:4x﹣z=29
④,
④×2+③得:9x=90,
解得x=10,
故选:C.
9.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有三个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有一个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
故四条直线在平面内交点的个数是0或1或3或4或5或6;
解方程ax+3=﹣9﹣x得x=﹣,
∵x是负整数,a是整数,
∴a+1=1或2或3或4或6或12,
解得a=0或1或2或3或5或11.
综上所述,a=0或1或3或5,满足条件的所有a的个数为4.
故选:B.
10.解:如图,
令y=|x|和y=ax+1,
而函数y=ax+1必过点(0,1),
∵方程|x|=ax+1有一个负根而且没有正根,
∴直线y=ax+1与函数y=|x|在第二象限只有交点,
∴a≥1,
故选:C.
二.填空题
11.解:,
①+②得:x﹣2y=﹣5,
②+③得:x﹣y=﹣2,
方程组为,
故答案为:.
12.解:依题意,得:4x+5y=196.
故答案为:4x+5y=196.
13.解:设A、B和C商品的单价分别为x,y和z元,
根据题意可列方程,
由①+②得,
8x+8y+8z=888,
化简得x+y+z=111.
答:购A、B、C各一件共需
111元
14.解:设这个数是x,
依题意得:
x=,
将未知数系数化为1得:x=.
故答案为:.
15.解:由题意,得:
,
即,
∴x2﹣y2=(x+y)(x﹣y)=5×(﹣3)=﹣15,
故答案为:﹣15.
16.解:设这个两位数的十位数字为x,个位数字为y,
依题意,得:,
解得:,
∴10x+y=85.
故答案为85.
17.解:根据题意得:2x﹣3+1=0,
移项合并得:2x=2,
解得:x=1.
故答案为:1.
18.解:把代入方程得:6﹣6a=16,
解得:a=﹣.
故答案为:﹣.
19.解:根据甲、乙两种型号的帐篷共2000顶,得方程x+y=2000;
根据共安置9000人,得方程6x+4y=9000.
列方程组为.
故答案为:.
20.解:设A组工作x天,B组工作(x+m+)天,C组工作(x+m++n+)天,(x,m,n都是正整数,且m≥1,n≥1),
则x+m+n<15,
根据题意得,
,
由①得,x=2m+1③,
由②得,5x=4m+4n+3④,
④﹣5×③得,n=,
∵m,n是正整数,
∴当m=1时,n=2,x=3,
∴m+n+x=6,符合题意,
当m=3时,n=5,x=7,
∴m+n+x=15,不符合题意,
即:A组工作3天,
∴一共生产了1080×3=3240瓶消毒液,
∴该医用超市一共订购了:=1620(件),
故答案为:1620.
三.解答题
21.解:∵|x+y﹣2020|=﹣|2020﹣x﹣y|,
∴,
即x+y=2020,
,
(①+②)÷3得,x+y=﹣,
∴﹣=2020
解得m=﹣6061.
22.解:设这个数为x,
依题意得:x﹣x+=,
移项得:x﹣x=﹣,
通分得:x﹣x=﹣,
合并同类项得:
x=,
将未知项的系数化为1得:x=.
答:这个数为.
23.解:(1)根据题意得,解得,
∴a,b,c的值分别为1,﹣4,3.
(2)当x=1时,x2﹣4x+3=1﹣4+3=0,
当x=4时,x2﹣4x+3=16﹣16+3=3;
∴m=0,n=3,
故答案为0,3;
(3)因为抛物线y=x2﹣4x+3的开口向上,当1<x<3时,y<0.
24.解:(1)设七年级1有x名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1有49名学生,2班有53名学生;
(2)设八年级报名x人,九年级报名y人,
分两种情况:
①若x+y<100,
由题意得:,
解得:,(不合题意舍去);
②若x+y≥100,
由题意得:,,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.
25.解:(1)400×=100(箱),
答:甲货车中药品100箱;
(2)400×(1+)=600(箱),600×=300(箱),
答:乙货车中食品有300箱;
(3)甲货车和乙货车共有:400+600=1000(箱),1000×=280(箱),
设甲货车中日用品为x箱,乙货车中日用品为y箱,
由题意得:,
解得:,
即甲货车中日用品为120箱,
则甲货车中食品的箱数为:400﹣100﹣120=180(箱),
答:甲货车中食品有180箱.
26.解:依题意,得
|m﹣2|﹣2=1,且m﹣3≠0、m+1≠0,
解得m=5.
故m的值是5.
27.解:(1)﹣23×(1﹣)÷0.5
=﹣8×÷
=﹣8××2
=﹣12;
(2)(﹣﹣)÷﹣2
=(﹣﹣)×36﹣2
=×36﹣×36﹣×36﹣2
=33﹣28﹣10﹣2
=﹣7;
(3)3(20﹣y)=6y﹣4(y﹣11).
去括号,得
60﹣3y=6y﹣4y+44.
移项及合并同类项,得
﹣5y=﹣16.
系数化为1,得
y=;
(4)﹣1=﹣.
去分母,得
3(2x+1)﹣12=2x﹣4(5x﹣1).
去括号,得
6x+3﹣12=2x﹣20x+4.
移项及合并同类项,得
24x=13.
系数化为1,得
x=.
一次方程与方程组》单元测试卷
一.选择题
1.下列各式中,是方程的是( )
A.
B.14﹣5=9
C.a>3b
D.x=1
2.下列方程中,是二元一次方程的是( )
A.xy=2
B.3x=4y
C.x+=2
D.x2+2y=4
3.根据等式的性质,下列选项中等式不一定成立的是( )
A.若a=b,则a+2=b+2
B.若ax=bx,则a=b
C.若=,则x=y
D.若3a=3b,则a=b
4.方程x+y=4与2x﹣3y=3的公共解是( )
A.
B.
C.
D.
5.若关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值为
( )
A.
B.
C.
D.
6.陈老师为学校购买运动会的奖品后,回学校向后勤处王老师交账说:“我买了两种书共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定弄错了.”陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,那么笔记本的单价可能是( )元.
A.1元
B.2元
C.3元
D.4元
7.某理财产品的年收益率为5.21%,若张老师购买x万元该种理财产品,定期2年,则2年后连同本金共有10万元,则根据题意列方程正确的是( )
A.(1+5.21)x=10
B.(1+5.21)2x=10
C.(1+5.21%)x=10
D.(1+5.21%)2x=10
8.解方程组得x等于( )
A.18
B.11
C.10
D.9
9.若整数a使关于x的方程ax+3=﹣9﹣x有负整数解,且a也是四条直线在平面内交点的个数,则满足条件的所有a的个数为( )
A.3
B.4
C.5
D.6
10.已知方程|x|=ax+1有一个负根而且没有正根,那么a的取值范围是( )
A.a>﹣1
B.a=1
C.a≥1
D.非上述答案
二.填空题
11.把三元一次方程组化为二元一次方程组
.
12.一支部队第一天行军4小时,第二天行军5小时,两天共行军196千米,如果设第一天每小时行军x千米,第二天每小时行军y千米,依题意,可列方程为
.
13.有A、B、C三种商品,如果购5件A、2件B、3件C共需513元,购3件A、6件B、5件C共需375元,那么购A、B、C各一件共需
元.
14.一个数的是,那么这个数是
.
15.若|x+y﹣5|+(x﹣y+3)2=0,则x2﹣y2=
.
16.一个两位数的十位数字与个位数字的和是13,把这个两位数减去27,结果恰好成为数字对调后组成的两位数,则这个两位数为
.
17.若2x﹣3与1互为相反数,则x=
.
18.如果是方程2x﹣3ay=16的一组解,则a=
.
19.2020年春节前夕“新型冠状病毒”爆发,某乡镇急需值班帐篷.某企业急灾区之所急,准备捐助甲、乙两种型号的帐篷2000顶,其中甲种帐篷每顶可安置6人,乙种帐篷每顶可安置4人,该企业捐助的帐篷共可安置9000人,设该企业捐助甲种帐篷x顶、乙种帐篷y顶,可列出的方程组为
.
20.2020年,受到新冠疫情的影响,全国市民都会佩戴口罩和配备一些消毒物品出门.某工厂生产的一种消毒套装深受市民喜爱,已知该消毒套装一套包含有2瓶消毒液,4包消毒湿巾,6个医用口罩,某医用超市向该厂订购了一批消毒套装,需要厂家在15天内生产完该套装并交货.该工厂将员工分为A、B、C三个组,分别对应生产消毒液、消毒湿巾、医用口罩;他们于某天零点开始工作,每天24小时轮班连续工作(假设每小时工作效率相同),若干天后的零点A组完成任务,再过几天后(不少于一天)的中午12点B组完成任务,再过几天(不少于一天)后的6时C组完成任务.已知A、B、C三个组每天完成的任务数分别是1080瓶,1440包,1440个,则该医用超市一共订购了
件消毒套装.
三.解答题
21.已知m满足,且满足|x+y﹣2020|=﹣|2020﹣x﹣y|,求m的值.
22.一个数减去它的,再加上等于,求这个数.
23.下表给出了代数式ax2+bx+c与x的一些对应值:
x
…
0
1
2
3
4
…
ax2+bx+c
…
3
m
﹣1
0
n
…
(1)利用表中所给数值求出a,b,c的值;
(2)直接写出:m=
,n=
;
(3)设y=ax2+bx+c,则当x取何值时,y<0.
24.某景点的门票价格如下表:
购票人数(人)
1~50
51~99
100以上(含100)
门票单价(元)
48
45
42
(1)某校七年级1、2两个班共有102人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
25.哈美加在疫情期间决定往灾区捐赠物资,租用了甲和乙两种型号的货车,将已经装箱的药品、食品、日用品运往灾区,每辆车中均装有药品、食品、日用品,其中甲货车总共装箱400箱,药品的箱数占甲车总箱数的.
(1)甲货车中药品多少箱?
(2)若乙货车的总箱数比甲货车的总箱数多,且乙货车中食品箱数占乙货车总箱数的一半,求乙货车中食品有多少箱?
(3)在(1)、(2)的条件下,甲货车中日用品的箱数是乙货车中日用品的箱数的,到灾区两车救灾物资在一起,此时日用品的箱数占两车总箱数的,求甲货车中食品有多少箱?
26.已知方程组是二元一次方程组,求m的值.
27.计算
(1)﹣23×(1﹣)÷0.5
(2)(﹣﹣)÷﹣2
(3)3(20﹣y)=6y﹣4(y﹣11)
(4)﹣1=﹣
参考答案与试题解析
一.选择题
1.解:A、没有等号,故不是方程,故此选项错误;
B、等式中没有未知数,不是方程,故此选项错误;
C、是不等式,不是方程,故此选项错误;
D、符合方程的定义,是方程,故此选项正确;
故选:D.
2.解:A、是二元二次方程,故本选项不符合题意;
B、是二元一次方程,故本选项符合题意;
C、不是整式方程,故本选项不符合题意;
D、是二元二次方程,故本选项不符合题意;
故选:B.
3.解:∵若a=b,则a+2=b+2,
∴选项A不符合题意;
∵若ax=bx,则x=0时,a可以不等于b,
∴选项B符合题意;
∵若=,则x=y,
∴选项C不符合题意;
∵若3a=3b,则a=b,
∴选项D不符合题意.
故选:B.
4.解:联立得:,
①×3+②得:5x=15,
解得:x=3,
把x=3代入①得:y=1,
则方程组的解为.
故选:B.
5.解:,
①+②,得2x=10k.
∴x=5k.
①﹣②,得2y=﹣4k,
∴y=﹣2k.
∵二元一次方程组的解也是二元一次方程2x+3y=6的解,
∴2×5k+3×(﹣2k)=6.
即4k=6,
∴k=.
故选:B.
6.解:设购买单价为8元的书x本,笔记本的单价为y元,则购买单价为12元的书(105﹣x)本,
依题意,得:8x+y+12(105﹣x)=1500﹣418,
∴y=178﹣4x,
又∵x,y均为正整数,且y<5,
∴x=44,y=2.
故选:B.
7.解:设张老师购买x万元该种理财产品,
可得:(1+5.21%)2x=10,
故选:D.
8.解:,
①×2﹣②得:4x﹣z=29
④,
④×2+③得:9x=90,
解得x=10,
故选:C.
9.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有三个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有一个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
故四条直线在平面内交点的个数是0或1或3或4或5或6;
解方程ax+3=﹣9﹣x得x=﹣,
∵x是负整数,a是整数,
∴a+1=1或2或3或4或6或12,
解得a=0或1或2或3或5或11.
综上所述,a=0或1或3或5,满足条件的所有a的个数为4.
故选:B.
10.解:如图,
令y=|x|和y=ax+1,
而函数y=ax+1必过点(0,1),
∵方程|x|=ax+1有一个负根而且没有正根,
∴直线y=ax+1与函数y=|x|在第二象限只有交点,
∴a≥1,
故选:C.
二.填空题
11.解:,
①+②得:x﹣2y=﹣5,
②+③得:x﹣y=﹣2,
方程组为,
故答案为:.
12.解:依题意,得:4x+5y=196.
故答案为:4x+5y=196.
13.解:设A、B和C商品的单价分别为x,y和z元,
根据题意可列方程,
由①+②得,
8x+8y+8z=888,
化简得x+y+z=111.
答:购A、B、C各一件共需
111元
14.解:设这个数是x,
依题意得:
x=,
将未知数系数化为1得:x=.
故答案为:.
15.解:由题意,得:
,
即,
∴x2﹣y2=(x+y)(x﹣y)=5×(﹣3)=﹣15,
故答案为:﹣15.
16.解:设这个两位数的十位数字为x,个位数字为y,
依题意,得:,
解得:,
∴10x+y=85.
故答案为85.
17.解:根据题意得:2x﹣3+1=0,
移项合并得:2x=2,
解得:x=1.
故答案为:1.
18.解:把代入方程得:6﹣6a=16,
解得:a=﹣.
故答案为:﹣.
19.解:根据甲、乙两种型号的帐篷共2000顶,得方程x+y=2000;
根据共安置9000人,得方程6x+4y=9000.
列方程组为.
故答案为:.
20.解:设A组工作x天,B组工作(x+m+)天,C组工作(x+m++n+)天,(x,m,n都是正整数,且m≥1,n≥1),
则x+m+n<15,
根据题意得,
,
由①得,x=2m+1③,
由②得,5x=4m+4n+3④,
④﹣5×③得,n=,
∵m,n是正整数,
∴当m=1时,n=2,x=3,
∴m+n+x=6,符合题意,
当m=3时,n=5,x=7,
∴m+n+x=15,不符合题意,
即:A组工作3天,
∴一共生产了1080×3=3240瓶消毒液,
∴该医用超市一共订购了:=1620(件),
故答案为:1620.
三.解答题
21.解:∵|x+y﹣2020|=﹣|2020﹣x﹣y|,
∴,
即x+y=2020,
,
(①+②)÷3得,x+y=﹣,
∴﹣=2020
解得m=﹣6061.
22.解:设这个数为x,
依题意得:x﹣x+=,
移项得:x﹣x=﹣,
通分得:x﹣x=﹣,
合并同类项得:
x=,
将未知项的系数化为1得:x=.
答:这个数为.
23.解:(1)根据题意得,解得,
∴a,b,c的值分别为1,﹣4,3.
(2)当x=1时,x2﹣4x+3=1﹣4+3=0,
当x=4时,x2﹣4x+3=16﹣16+3=3;
∴m=0,n=3,
故答案为0,3;
(3)因为抛物线y=x2﹣4x+3的开口向上,当1<x<3时,y<0.
24.解:(1)设七年级1有x名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1有49名学生,2班有53名学生;
(2)设八年级报名x人,九年级报名y人,
分两种情况:
①若x+y<100,
由题意得:,
解得:,(不合题意舍去);
②若x+y≥100,
由题意得:,,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.
25.解:(1)400×=100(箱),
答:甲货车中药品100箱;
(2)400×(1+)=600(箱),600×=300(箱),
答:乙货车中食品有300箱;
(3)甲货车和乙货车共有:400+600=1000(箱),1000×=280(箱),
设甲货车中日用品为x箱,乙货车中日用品为y箱,
由题意得:,
解得:,
即甲货车中日用品为120箱,
则甲货车中食品的箱数为:400﹣100﹣120=180(箱),
答:甲货车中食品有180箱.
26.解:依题意,得
|m﹣2|﹣2=1,且m﹣3≠0、m+1≠0,
解得m=5.
故m的值是5.
27.解:(1)﹣23×(1﹣)÷0.5
=﹣8×÷
=﹣8××2
=﹣12;
(2)(﹣﹣)÷﹣2
=(﹣﹣)×36﹣2
=×36﹣×36﹣×36﹣2
=33﹣28﹣10﹣2
=﹣7;
(3)3(20﹣y)=6y﹣4(y﹣11).
去括号,得
60﹣3y=6y﹣4y+44.
移项及合并同类项,得
﹣5y=﹣16.
系数化为1,得
y=;
(4)﹣1=﹣.
去分母,得
3(2x+1)﹣12=2x﹣4(5x﹣1).
去括号,得
6x+3﹣12=2x﹣20x+4.
移项及合并同类项,得
24x=13.
系数化为1,得
x=.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
