2020-2021学年沪科新版七年级上册数学《第4章 直线与角》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年沪科新版七年级上册数学《第4章 直线与角》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 00:00:00 | ||
图片预览




文档简介
2020-2021学年沪科新版七年级上册数学《第4章
直线与角》单元测试卷
一.选择题
1.下列语句错误的个数是( )
①一个角的补角不是锐角就是钝角;
②角是由两条射线组成的图形;
③如果点C是线段AB的中点,那么AB=2AC=2BC;
④连接两点之间的线段叫做两点的距离.
A.4个
B.3个
C.2个
D.1个
2.下列几何体都是由平面围成的是( )
A.圆柱
B.圆锥
C.四棱柱
D.球
3.如图:CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转
B.绕着AB旋转
C.绕着CD旋转
D.绕着BC旋转
4.如图,在平整的地面上,有若干个完全相同的棱长为2cm的小正方体堆成的一个几何体.如果在这个几何体的表面喷上红色的漆(贴紧地面的部分不喷),这个几何体喷漆的面积是( )
A.30cm2
B.32cm2
C.120cm2
D.128cm2
5.在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,圆规两脚之间的距离是( )厘米.
A.7
B.4
C.3.5
D.3
6.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3
B.1.5
C.1.2
D.1
7.下列语句中,叙述准确规范的是( )
A.直线a,b相交于点m
B.延长直线AB
C.线段ab与线段bc交于点b
D.延长线段AC至点B,使BC=AC
8.下列说法中,正确的是( )
A.绝对值等于他本身的数是正数
B.任何有理数的绝对值都不是负数
C.数轴上的点表示的数,左边的比右边的大
D.角的大小与角两边的长度有关,边越长角越大
9.甲、乙两个城市,乙城市位于甲城市北偏东50°方向,距离为80km,那么甲城市位于乙城市( )
A.南偏东50°方向,距离为80km
B.南偏西50°方向,距离为80km
C.南偏东40°方向,距离为80km
D.南偏西40°方向,距离为80km
10.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
二.填空题
11.如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,以适当的长为半径作弧,交AB于点M,交AC于点N.分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为
.
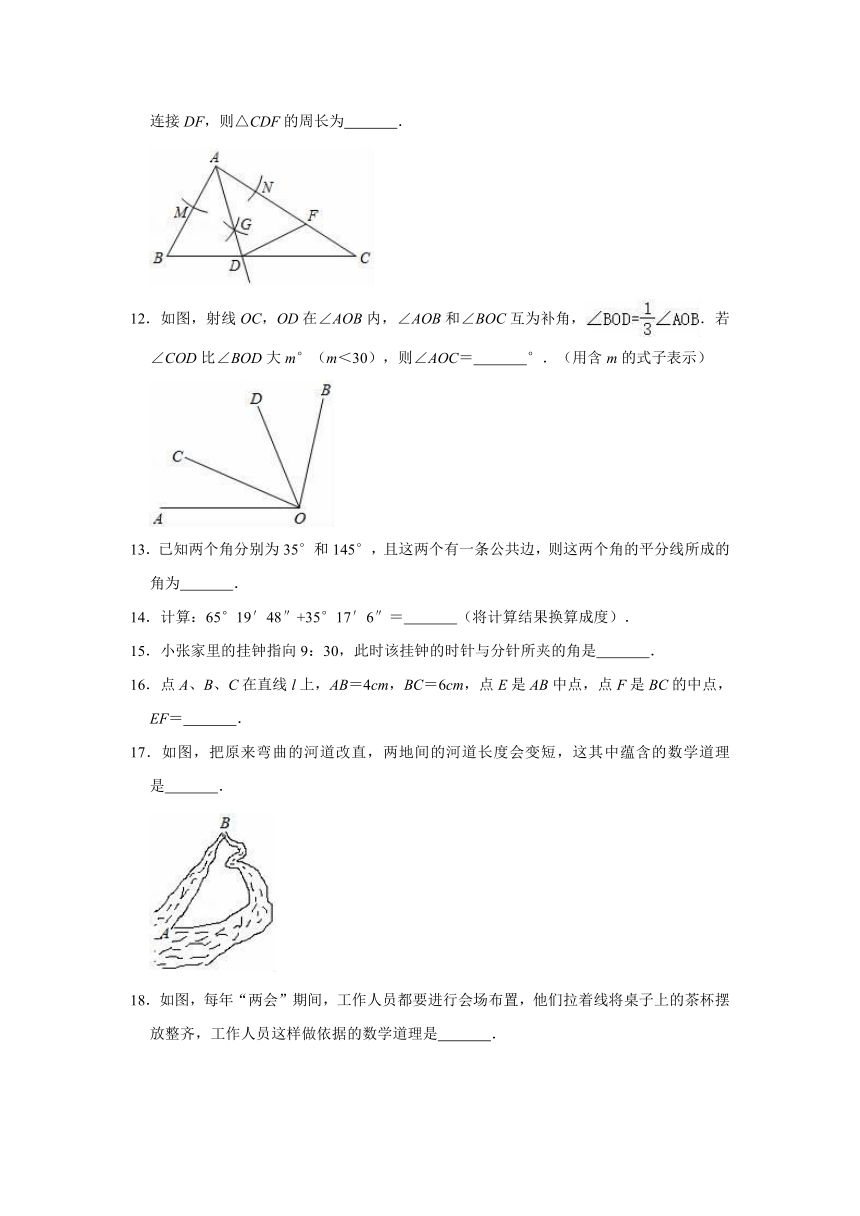
12.如图,射线OC,OD在∠AOB内,∠AOB和∠BOC互为补角,.若∠COD比∠BOD大m°(m<30),则∠AOC=
°.(用含m的式子表示)
13.已知两个角分别为35°和145°,且这两个有一条公共边,则这两个角的平分线所成的角为
.
14.计算:65°19′48″+35°17′6″=
(将计算结果换算成度).
15.小张家里的挂钟指向9:30,此时该挂钟的时针与分针所夹的角是
.
16.点A、B、C在直线l上,AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,EF=
.
17.如图,把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是
.
18.如图,每年“两会”期间,工作人员都要进行会场布置,他们拉着线将桌子上的茶杯摆放整齐,工作人员这样做依据的数学道理是
.
19.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是
.
20.如图,其中大圆半径为R,小圆半径为r,阴影部分的面积
.(结果保留π)
三.解答题
21.如图,请度量出需要的数据,并计算阴影部分的面积.
22.如图,在平面内有A,B,C三点.
(1)画直线AB,射线AC,线段BC;
(2)在线段BC上任取一点D(不同于B,C),连接AD,并延长AD至E,使DE=AD;
(3)数一数,此时图中线段共有
条.
23.如图,点C在线段AB上,AB=9,AC=2CB,D是AC的中点,求AD长.
24.计算:
(1)131°28′﹣51°32′15″
(2)58°38′27″+47°42′40″
(3)34°25′×3+35°42′
25.如图1,已知∠AOB的内部有一条射线OC,OM、ON分别平分∠AOC和∠BOC.
(1)若∠AOB=120°,∠BOC=40°,求∠MON的度数.
(2)若取掉(1)中的条件∠BOC=40°,只保留∠AOB=120°,求∠MON的度数.
(3)若将∠AOB内部的射线OC旋转到∠AOB的外部,如图2,∠AOB=120°,求∠MON的度数,并请用一句话或一个式子概括你发现的∠MON与∠AOB的数量关系.
26.用如图所示的甲,乙,丙三块木板做一个长,宽,高分别为3a(cm),2a(cm)和20cm的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板锯成两块刚好能做一个长侧面和一个短侧面,丙块木板锯成两块刚好能做箱盖和剩下的一个短侧面(厚度忽略不计).
(1)用含a的代数式分别表示甲,乙,丙三块木板的面积(代数式要求化简);
(2)如果购买一块长12a(cm),宽120cm的长方形木板做这个箱子,那么只需用去这块木板的几分之几(用含a的代数式表示)?如果a=20呢?
27.点O是直线AB上一点,以O为端点画射线OC,OD,使∠AOC=60°,∠COD=90°,画出符合题意的两个图形,再求∠BOD的度数.
参考答案与试题解析
一.选择题
1.解:①直角的补角是直角,故原说法错误;
②角是由有公共的端点的两条射线组成的图形,故原说法错误;
③如果点C是线段AB的中点,那么AB=2AC=2BC,说法正确;
④连接两点之间的线段的长度叫做两点的距离,故原说法错误.
故错误的个数有①②④共3个.
故选:B.
2.解:圆柱的侧面是曲面,圆锥的侧面也是曲面,球是有曲面围成的,只有四棱柱是由6个平面围成的,
故选:C.
3.解:将直角三角形ABC绕斜边AB所在直线旋转一周得到的几何体是,
故选:B.
4.解:喷漆表面的面一共有32个,则这个几何体喷漆的面积为32×4=128(cm2),
故选:D.
5.解:∵在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,
∴这个最大的圆的直径=长方形的宽7厘米,
∴圆规两脚之间的距离是=3.5(厘米),
故选:C.
6.解:∵点C是AB的中点,AB=9,
∴AC=CB=AB=4.5,
当点D是AB的三等分点,点D在线段BC上时,BD=AB=3,
∴CD=4.5﹣3=1.5,
当点D是AB的三等分点,点D′在线段AC上时,AD′=AB=3,
∴CD′=4.5﹣3=1.5,
故选:B.
7.解:A.点应该用大写字母表示,直线a,b相交于点M,原说法错误,故本选项不符合题意;
B.直线向两端无限延伸,原说法错误,故本选项不符合题意;
C.线段不可以用两个小写字母表示,可以用一个小写字母表示,原说法错误,故本选项不符合题意;
D.可以延长线段AC至点B.使BC=AC,原说法正确,故本选项符合题意;
故选:D.
8.解:A、绝对值等于它本身的数是非负数,原说法错误,故此选项不符合题意;
B、任何有理数的绝对值都不是负数,原说法正确,故此选项符合题意;
C、数轴上的点表示的数,右边的比左边的大,原说法错误,故此选项不符合题意;
D、角的大小与角两边的长度无关,原说法错误,故此选项不符合题意;
故选:B.
9.解:如图:
∵乙城市位于甲城市北偏东50°方向,距离为80km,
∴甲城市位于乙城市南偏西50°方向,距离为80km,
故选:B.
10.解:∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
二.填空题
11.解:∵AB=5,AC=8,AF=AB,
∴FC=AC﹣AF=8﹣5=3,
由作图方法可得:AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△AFD中
,
∴△ABD≌△AFD(SAS),
∴BD=DF,
∴△DFC的周长为:DF+FC+DC=BD+DC+FC=BC+FC=9+3=12.
故答案为:12.
12.解:∵∠AOB和∠BOC互为补角,
∴∠AOB+∠BOC=180°,
∵∠BOD=,
∴3∠BOD+∠BOC=180°,
即∠BOC=180°﹣3∠BOD,
∵∠COD+∠BOD=∠BOC,
∴180°﹣3∠BOD=∠COD+∠BOD,
∴∠COD+4∠BOD=180°,
∵∠COD比∠BOD大m°(m<30),
∴∠COD﹣∠BOD=m°,
∴∠BOD=()°,∠COD=()°
∴∠BOC=()°,
∴∠AOB=180°﹣∠BOC=(108﹣)°,
∴∠AOC=∠AOB﹣∠BOC=(108﹣)°﹣()°=(36﹣m)°.
故答案为(36﹣m).
13.解:因为35°+145°=180°,且这两个有一条公共边,
所以互补的两个角有一条公共边,
当两个角有一个公共边,另一边在“公共边”的两侧时,则这两个角的平分线所成的角为=90°;
当两个角有一个公共边,另一边在“公共边”的同侧时,则这两个角的平分线所成的角为=55°.
故答案为:90°或55°.
14.解:65°19′48″+35°17′6″
=100°36′54″,
∵54÷60=0.9,(36+0.9)÷60=0.615,100+0.615=100.615,
∴100°36′54″=100.615°.
故答案是:100.615°.
15.解:3×30°+15°=105°.
∴钟面上9点30分时,分针与时针所成的角的度数是105°.
故答案为:105°.
16.解:如图,∵AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,
∴BE=AB=2cm,BF=BC=3cm,
①点B在A、C之间时,EF=BE+BF=2+3=5cm;
②点A在B、C之间时,EF=BF﹣BE=3﹣2=1cm.
∴EF的长等于5cm或1cm.
故答案为:5cm或1cm.
17.解:把原来弯曲的河道改直,两地间的河道长度会变短,
这其中蕴含的数学道理是两点之间线段最短.
故答案为:两点之间线段最短.
18.解:每年“两会”期间,工作人员都要进行会场布置,他们拉着线将桌子上的茶杯摆放整齐,工作人员这样做依据的数学道理是:两点确定一条直线,
故答案为:两点确定一条直线.
19.解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁,
故答案为:丁.
20.解:∵大圆的面积为πR2,小圆的面积为πr2,
∴阴影部分的面积为πR2﹣πr2=π(R2﹣r2),
故答案为:π(R2﹣r2).
三.解答题
21.解:测量可得半圆半径为2cm,扇形半径为4cm.
S半圆=3.14×22÷2=6.28(cm2),
S扇形=3.14×42÷4=12.56(cm2),
S阴影=12.56﹣6.28=6.28
(cm2).
22.解:(1)如图,直线AB,线段BC,射线AC即为所求;
(2)如图,线段AD和线段DE即为所求;
(3)由题可得,图中线段的条数为8,
故答案为:8.
23.解:∵点C在线段AB上,AC=2CB,AB=9,
∴AC=6,
∵D是AC的中点,
∴AD=AC,
∴AD=3.
24.解:(1)131°28′﹣51°32′15″=79°55′45″;
(2)58°38′27″+47°42′40″=106°21′7″;
(3)34°25′×3+35°42′
=103°15′+35°42′
=138°57′.
25.解:(1)∵∠AOB=120°,∠BOC=40°,
∴∠AOC=∠AOB﹣∠BOC=120°﹣40°=80°,
∵OM、ON分别平分∠AOC和∠BOC,
∴∠MOC=,,
∴∠MON=∠MOC+∠NOC=40°+20°=60°;
(2)∵OM、ON分别平分∠AOC和∠BOC,
∴∠MOC=,,
∵∠AOC+∠BOC=∠AOB,∠AOB=120°,
∴∠MON=∠MOC+∠NOC====60°;
(3)∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC,∠NOC=∠BOC,
所以∠MON=∠COM﹣∠CON=∠AOC﹣∠BOC=(∠AOC﹣∠BOC)==×120°=60°,
.
26.解:(1)由题意得:
甲木板的面积:3a×2a+3a×20=(6a2+60a)(cm2),
乙木板的面积:3a×20+2a×20=100a(cm2),
丙木板的面积:3a×2a+2a×20=(6a2+40a)(cm2);
(2)长12acm,宽120cm的长方形木板的面积:12a×120=1440a,
=,
当a=20时,==.
答:需用去这块木板的,当a=20时,用去这块木板的.
27.解:满足题意的情况有两种:
①当OC,OD在AB的同侧时,如图,∠BOD=180°﹣∠AOC﹣∠COD=30°;
②当OC,OD在AB的异侧时,如图,∠BOD=180°﹣(∠COD﹣∠AOC)=150°;
直线与角》单元测试卷
一.选择题
1.下列语句错误的个数是( )
①一个角的补角不是锐角就是钝角;
②角是由两条射线组成的图形;
③如果点C是线段AB的中点,那么AB=2AC=2BC;
④连接两点之间的线段叫做两点的距离.
A.4个
B.3个
C.2个
D.1个
2.下列几何体都是由平面围成的是( )
A.圆柱
B.圆锥
C.四棱柱
D.球
3.如图:CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转
B.绕着AB旋转
C.绕着CD旋转
D.绕着BC旋转
4.如图,在平整的地面上,有若干个完全相同的棱长为2cm的小正方体堆成的一个几何体.如果在这个几何体的表面喷上红色的漆(贴紧地面的部分不喷),这个几何体喷漆的面积是( )
A.30cm2
B.32cm2
C.120cm2
D.128cm2
5.在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,圆规两脚之间的距离是( )厘米.
A.7
B.4
C.3.5
D.3
6.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3
B.1.5
C.1.2
D.1
7.下列语句中,叙述准确规范的是( )
A.直线a,b相交于点m
B.延长直线AB
C.线段ab与线段bc交于点b
D.延长线段AC至点B,使BC=AC
8.下列说法中,正确的是( )
A.绝对值等于他本身的数是正数
B.任何有理数的绝对值都不是负数
C.数轴上的点表示的数,左边的比右边的大
D.角的大小与角两边的长度有关,边越长角越大
9.甲、乙两个城市,乙城市位于甲城市北偏东50°方向,距离为80km,那么甲城市位于乙城市( )
A.南偏东50°方向,距离为80km
B.南偏西50°方向,距离为80km
C.南偏东40°方向,距离为80km
D.南偏西40°方向,距离为80km
10.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
二.填空题
11.如图,在△ABC中,AB=5,AC=8,BC=9,以A为圆心,以适当的长为半径作弧,交AB于点M,交AC于点N.分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,点F在AC边上,AF=AB,连接DF,则△CDF的周长为
.
12.如图,射线OC,OD在∠AOB内,∠AOB和∠BOC互为补角,.若∠COD比∠BOD大m°(m<30),则∠AOC=
°.(用含m的式子表示)
13.已知两个角分别为35°和145°,且这两个有一条公共边,则这两个角的平分线所成的角为
.
14.计算:65°19′48″+35°17′6″=
(将计算结果换算成度).
15.小张家里的挂钟指向9:30,此时该挂钟的时针与分针所夹的角是
.
16.点A、B、C在直线l上,AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,EF=
.
17.如图,把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是
.
18.如图,每年“两会”期间,工作人员都要进行会场布置,他们拉着线将桌子上的茶杯摆放整齐,工作人员这样做依据的数学道理是
.
19.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是
.
20.如图,其中大圆半径为R,小圆半径为r,阴影部分的面积
.(结果保留π)
三.解答题
21.如图,请度量出需要的数据,并计算阴影部分的面积.
22.如图,在平面内有A,B,C三点.
(1)画直线AB,射线AC,线段BC;
(2)在线段BC上任取一点D(不同于B,C),连接AD,并延长AD至E,使DE=AD;
(3)数一数,此时图中线段共有
条.
23.如图,点C在线段AB上,AB=9,AC=2CB,D是AC的中点,求AD长.
24.计算:
(1)131°28′﹣51°32′15″
(2)58°38′27″+47°42′40″
(3)34°25′×3+35°42′
25.如图1,已知∠AOB的内部有一条射线OC,OM、ON分别平分∠AOC和∠BOC.
(1)若∠AOB=120°,∠BOC=40°,求∠MON的度数.
(2)若取掉(1)中的条件∠BOC=40°,只保留∠AOB=120°,求∠MON的度数.
(3)若将∠AOB内部的射线OC旋转到∠AOB的外部,如图2,∠AOB=120°,求∠MON的度数,并请用一句话或一个式子概括你发现的∠MON与∠AOB的数量关系.
26.用如图所示的甲,乙,丙三块木板做一个长,宽,高分别为3a(cm),2a(cm)和20cm的长方体木箱,其中甲块木板锯成两块刚好能做箱底和一个长侧面,乙块木板锯成两块刚好能做一个长侧面和一个短侧面,丙块木板锯成两块刚好能做箱盖和剩下的一个短侧面(厚度忽略不计).
(1)用含a的代数式分别表示甲,乙,丙三块木板的面积(代数式要求化简);
(2)如果购买一块长12a(cm),宽120cm的长方形木板做这个箱子,那么只需用去这块木板的几分之几(用含a的代数式表示)?如果a=20呢?
27.点O是直线AB上一点,以O为端点画射线OC,OD,使∠AOC=60°,∠COD=90°,画出符合题意的两个图形,再求∠BOD的度数.
参考答案与试题解析
一.选择题
1.解:①直角的补角是直角,故原说法错误;
②角是由有公共的端点的两条射线组成的图形,故原说法错误;
③如果点C是线段AB的中点,那么AB=2AC=2BC,说法正确;
④连接两点之间的线段的长度叫做两点的距离,故原说法错误.
故错误的个数有①②④共3个.
故选:B.
2.解:圆柱的侧面是曲面,圆锥的侧面也是曲面,球是有曲面围成的,只有四棱柱是由6个平面围成的,
故选:C.
3.解:将直角三角形ABC绕斜边AB所在直线旋转一周得到的几何体是,
故选:B.
4.解:喷漆表面的面一共有32个,则这个几何体喷漆的面积为32×4=128(cm2),
故选:D.
5.解:∵在一个长8厘米,宽7厘米的长方形里面画一个最大的圆,
∴这个最大的圆的直径=长方形的宽7厘米,
∴圆规两脚之间的距离是=3.5(厘米),
故选:C.
6.解:∵点C是AB的中点,AB=9,
∴AC=CB=AB=4.5,
当点D是AB的三等分点,点D在线段BC上时,BD=AB=3,
∴CD=4.5﹣3=1.5,
当点D是AB的三等分点,点D′在线段AC上时,AD′=AB=3,
∴CD′=4.5﹣3=1.5,
故选:B.
7.解:A.点应该用大写字母表示,直线a,b相交于点M,原说法错误,故本选项不符合题意;
B.直线向两端无限延伸,原说法错误,故本选项不符合题意;
C.线段不可以用两个小写字母表示,可以用一个小写字母表示,原说法错误,故本选项不符合题意;
D.可以延长线段AC至点B.使BC=AC,原说法正确,故本选项符合题意;
故选:D.
8.解:A、绝对值等于它本身的数是非负数,原说法错误,故此选项不符合题意;
B、任何有理数的绝对值都不是负数,原说法正确,故此选项符合题意;
C、数轴上的点表示的数,右边的比左边的大,原说法错误,故此选项不符合题意;
D、角的大小与角两边的长度无关,原说法错误,故此选项不符合题意;
故选:B.
9.解:如图:
∵乙城市位于甲城市北偏东50°方向,距离为80km,
∴甲城市位于乙城市南偏西50°方向,距离为80km,
故选:B.
10.解:∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
二.填空题
11.解:∵AB=5,AC=8,AF=AB,
∴FC=AC﹣AF=8﹣5=3,
由作图方法可得:AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△AFD中
,
∴△ABD≌△AFD(SAS),
∴BD=DF,
∴△DFC的周长为:DF+FC+DC=BD+DC+FC=BC+FC=9+3=12.
故答案为:12.
12.解:∵∠AOB和∠BOC互为补角,
∴∠AOB+∠BOC=180°,
∵∠BOD=,
∴3∠BOD+∠BOC=180°,
即∠BOC=180°﹣3∠BOD,
∵∠COD+∠BOD=∠BOC,
∴180°﹣3∠BOD=∠COD+∠BOD,
∴∠COD+4∠BOD=180°,
∵∠COD比∠BOD大m°(m<30),
∴∠COD﹣∠BOD=m°,
∴∠BOD=()°,∠COD=()°
∴∠BOC=()°,
∴∠AOB=180°﹣∠BOC=(108﹣)°,
∴∠AOC=∠AOB﹣∠BOC=(108﹣)°﹣()°=(36﹣m)°.
故答案为(36﹣m).
13.解:因为35°+145°=180°,且这两个有一条公共边,
所以互补的两个角有一条公共边,
当两个角有一个公共边,另一边在“公共边”的两侧时,则这两个角的平分线所成的角为=90°;
当两个角有一个公共边,另一边在“公共边”的同侧时,则这两个角的平分线所成的角为=55°.
故答案为:90°或55°.
14.解:65°19′48″+35°17′6″
=100°36′54″,
∵54÷60=0.9,(36+0.9)÷60=0.615,100+0.615=100.615,
∴100°36′54″=100.615°.
故答案是:100.615°.
15.解:3×30°+15°=105°.
∴钟面上9点30分时,分针与时针所成的角的度数是105°.
故答案为:105°.
16.解:如图,∵AB=4cm,BC=6cm,点E是AB中点,点F是BC的中点,
∴BE=AB=2cm,BF=BC=3cm,
①点B在A、C之间时,EF=BE+BF=2+3=5cm;
②点A在B、C之间时,EF=BF﹣BE=3﹣2=1cm.
∴EF的长等于5cm或1cm.
故答案为:5cm或1cm.
17.解:把原来弯曲的河道改直,两地间的河道长度会变短,
这其中蕴含的数学道理是两点之间线段最短.
故答案为:两点之间线段最短.
18.解:每年“两会”期间,工作人员都要进行会场布置,他们拉着线将桌子上的茶杯摆放整齐,工作人员这样做依据的数学道理是:两点确定一条直线,
故答案为:两点确定一条直线.
19.解:将如图所示的图形剪去一个小正方形,使余下的部分不能围成一个正方体,编号为甲乙丙丁的小正方形中剪去的是丁,
故答案为:丁.
20.解:∵大圆的面积为πR2,小圆的面积为πr2,
∴阴影部分的面积为πR2﹣πr2=π(R2﹣r2),
故答案为:π(R2﹣r2).
三.解答题
21.解:测量可得半圆半径为2cm,扇形半径为4cm.
S半圆=3.14×22÷2=6.28(cm2),
S扇形=3.14×42÷4=12.56(cm2),
S阴影=12.56﹣6.28=6.28
(cm2).
22.解:(1)如图,直线AB,线段BC,射线AC即为所求;
(2)如图,线段AD和线段DE即为所求;
(3)由题可得,图中线段的条数为8,
故答案为:8.
23.解:∵点C在线段AB上,AC=2CB,AB=9,
∴AC=6,
∵D是AC的中点,
∴AD=AC,
∴AD=3.
24.解:(1)131°28′﹣51°32′15″=79°55′45″;
(2)58°38′27″+47°42′40″=106°21′7″;
(3)34°25′×3+35°42′
=103°15′+35°42′
=138°57′.
25.解:(1)∵∠AOB=120°,∠BOC=40°,
∴∠AOC=∠AOB﹣∠BOC=120°﹣40°=80°,
∵OM、ON分别平分∠AOC和∠BOC,
∴∠MOC=,,
∴∠MON=∠MOC+∠NOC=40°+20°=60°;
(2)∵OM、ON分别平分∠AOC和∠BOC,
∴∠MOC=,,
∵∠AOC+∠BOC=∠AOB,∠AOB=120°,
∴∠MON=∠MOC+∠NOC====60°;
(3)∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOC,∠NOC=∠BOC,
所以∠MON=∠COM﹣∠CON=∠AOC﹣∠BOC=(∠AOC﹣∠BOC)==×120°=60°,
.
26.解:(1)由题意得:
甲木板的面积:3a×2a+3a×20=(6a2+60a)(cm2),
乙木板的面积:3a×20+2a×20=100a(cm2),
丙木板的面积:3a×2a+2a×20=(6a2+40a)(cm2);
(2)长12acm,宽120cm的长方形木板的面积:12a×120=1440a,
=,
当a=20时,==.
答:需用去这块木板的,当a=20时,用去这块木板的.
27.解:满足题意的情况有两种:
①当OC,OD在AB的同侧时,如图,∠BOD=180°﹣∠AOC﹣∠COD=30°;
②当OC,OD在AB的异侧时,如图,∠BOD=180°﹣(∠COD﹣∠AOC)=150°;
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
