苏科版七年级数学上册同步练习3.3代数式的值第1课时代数式的值(word版含答案解析)
文档属性
| 名称 | 苏科版七年级数学上册同步练习3.3代数式的值第1课时代数式的值(word版含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 320.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览


文档简介
苏科版七年级数学上第3章代数式3.3代数式的值第1课时代数式的值
一、选择题(共5小题;共25分)
1.
已知
,,则代数式
的值为
A.
B.
C.
D.
2.
已知
,
互为相反数,,
互为倒数,则代数式
的值为
A.
B.
C.
D.
3.
若
是
的相反数,,则
的值为
A.
B.
C.
或
D.
或
4.
若
,则
的值为
A.
B.
C.
D.
5.
关于代数式
的值,下列说法错误的是
A.
当
时,其值为
B.
当
时,其值不存在
C.
当
时,其值存在
D.
当
时,其值为
二、填空题(共7小题;共35分)
6.
已知
,则代数式
?.
7.
小张在计算
的值时,误将“”看成“”,结果得
,那么
的正确结果应为
?.
8.
当
时,代数式
的值为
?.
9.
填在下面各正方形中的四个数之间都有一定的规律,据此规律得出
?.
10.
若
,则
?.
11.
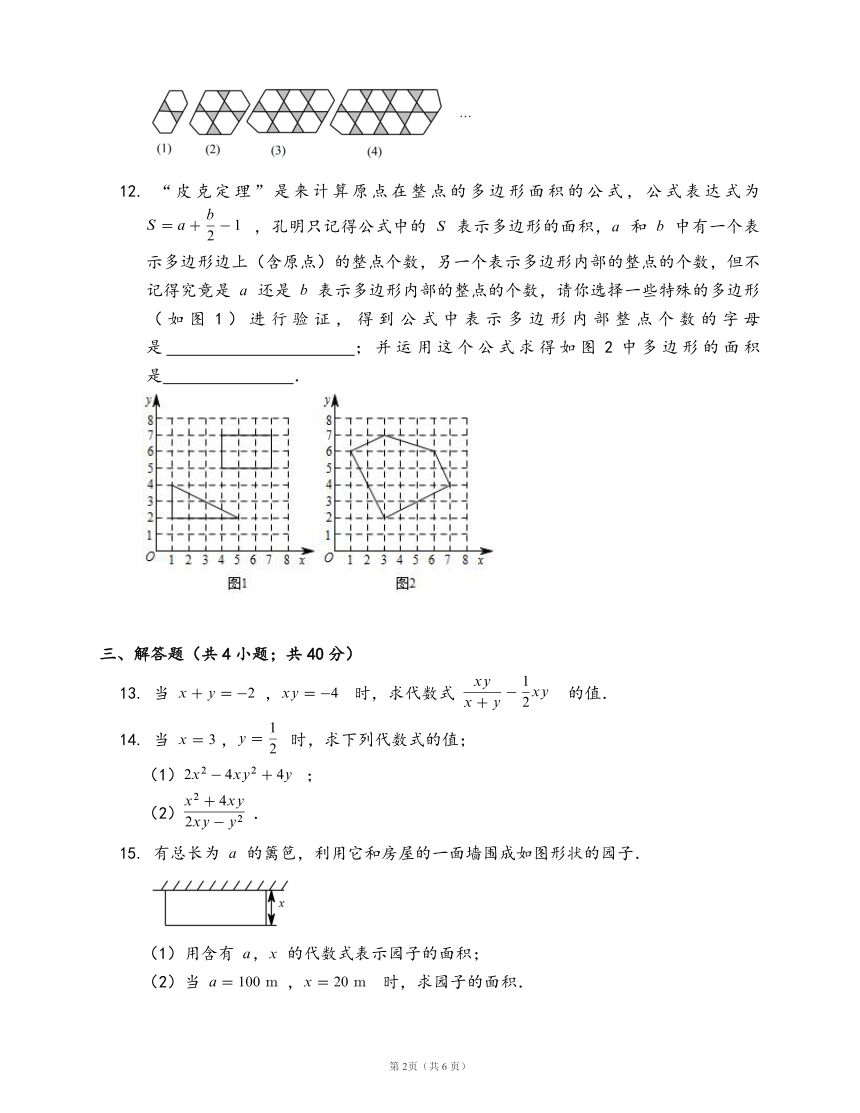
如图是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案,则第
个图案中阴影小三角形的个数是
?.
12.
“皮克定理”是来计算原点在整点的多边形面积的公式,公式表达式为
,孔明只记得公式中的
表示多边形的面积,
和
中有一个表示多边形边上(含原点)的整点个数,另一个表示多边形内部的整点的个数,但不记得究竟是
还是
表示多边形内部的整点的个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部整点个数的字母是
?;并运用这个公式求得如图2中多边形的面积是
?.
三、解答题(共4小题;共40分)
13.
当
,
时,求代数式
的值.
14.
当
,
时,求下列代数式的值;
(1);
(2).
15.
有总长为
的篱笆,利用它和房屋的一面墙围成如图形状的园子.
(1)用含有
,
的代数式表示园子的面积;
(2)当
,
时,求园子的面积.
16.
当
时,代数式
的值为
,求当
时,代数式
的值.
答案
第一部分
1.
B
2.
C
3.
D
4.
B
【解析】因为
,
且
,
所以
,,
所以
,,
所以
.
5.
D
【解析】当
时,代入代数式可得代数式的值为
.
第二部分
6.
【解析】将
整体代入可得
.
7.
【解析】由小张在计算
的值时,误将“”看成“”,结果得
,可知
,
,
.
8.
9.
【解析】左上角数的规律为偶数依次排列,右上角数为奇数依次排列,
所以
,
,
所以
,
观察前三个正方形,得
,
所以
.
10.
【解析】先将
化为与
有关的式子,再整体代入求值.;也可以由
,得到
,然后代入
得
,结果也是
.
11.
【解析】由图可知:第
个图案有阴影小三角形
个.第
个图案有阴影小三角形
(个).第
个图案有阴影小三角形
(个),第
个图案有阴影小三角形
(个),,那么第
个图案有阴影小三角形
个.
12.
,
【解析】
三角形内有
个格点,边上有
个格点,面积为
,即
,
矩形内有
个格点,边上有
个格点,面积为
,即
;
公式中表示多边形内部整点个数的字母是
.
由图2可知,,,故
.
第三部分
13.
当
,
时,
.
14.
(1)
当
,
时,
??????(2)
当
,
时,
15.
(1)
园子的面积为
.
??????(2)
当
,
时,
,
故园子的面积为
.
16.
因为
,
当
时,,
得到
,
所以
.
当
时,.
第1页(共6
页)
一、选择题(共5小题;共25分)
1.
已知
,,则代数式
的值为
A.
B.
C.
D.
2.
已知
,
互为相反数,,
互为倒数,则代数式
的值为
A.
B.
C.
D.
3.
若
是
的相反数,,则
的值为
A.
B.
C.
或
D.
或
4.
若
,则
的值为
A.
B.
C.
D.
5.
关于代数式
的值,下列说法错误的是
A.
当
时,其值为
B.
当
时,其值不存在
C.
当
时,其值存在
D.
当
时,其值为
二、填空题(共7小题;共35分)
6.
已知
,则代数式
?.
7.
小张在计算
的值时,误将“”看成“”,结果得
,那么
的正确结果应为
?.
8.
当
时,代数式
的值为
?.
9.
填在下面各正方形中的四个数之间都有一定的规律,据此规律得出
?.
10.
若
,则
?.
11.
如图是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案,则第
个图案中阴影小三角形的个数是
?.
12.
“皮克定理”是来计算原点在整点的多边形面积的公式,公式表达式为
,孔明只记得公式中的
表示多边形的面积,
和
中有一个表示多边形边上(含原点)的整点个数,另一个表示多边形内部的整点的个数,但不记得究竟是
还是
表示多边形内部的整点的个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部整点个数的字母是
?;并运用这个公式求得如图2中多边形的面积是
?.
三、解答题(共4小题;共40分)
13.
当
,
时,求代数式
的值.
14.
当
,
时,求下列代数式的值;
(1);
(2).
15.
有总长为
的篱笆,利用它和房屋的一面墙围成如图形状的园子.
(1)用含有
,
的代数式表示园子的面积;
(2)当
,
时,求园子的面积.
16.
当
时,代数式
的值为
,求当
时,代数式
的值.
答案
第一部分
1.
B
2.
C
3.
D
4.
B
【解析】因为
,
且
,
所以
,,
所以
,,
所以
.
5.
D
【解析】当
时,代入代数式可得代数式的值为
.
第二部分
6.
【解析】将
整体代入可得
.
7.
【解析】由小张在计算
的值时,误将“”看成“”,结果得
,可知
,
,
.
8.
9.
【解析】左上角数的规律为偶数依次排列,右上角数为奇数依次排列,
所以
,
,
所以
,
观察前三个正方形,得
,
所以
.
10.
【解析】先将
化为与
有关的式子,再整体代入求值.;也可以由
,得到
,然后代入
得
,结果也是
.
11.
【解析】由图可知:第
个图案有阴影小三角形
个.第
个图案有阴影小三角形
(个).第
个图案有阴影小三角形
(个),第
个图案有阴影小三角形
(个),,那么第
个图案有阴影小三角形
个.
12.
,
【解析】
三角形内有
个格点,边上有
个格点,面积为
,即
,
矩形内有
个格点,边上有
个格点,面积为
,即
;
公式中表示多边形内部整点个数的字母是
.
由图2可知,,,故
.
第三部分
13.
当
,
时,
.
14.
(1)
当
,
时,
??????(2)
当
,
时,
15.
(1)
园子的面积为
.
??????(2)
当
,
时,
,
故园子的面积为
.
16.
因为
,
当
时,,
得到
,
所以
.
当
时,.
第1页(共6
页)
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
