人教版七年级数学上册教学课件-3.4 .1实际问题与一元一次方程——配套问题(22张)
文档属性
| 名称 | 人教版七年级数学上册教学课件-3.4 .1实际问题与一元一次方程——配套问题(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 420.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 12:16:28 | ||
图片预览






文档简介
(共22张PPT)
3.4.1实际问题与一元一次方程
——配套问题
人教版
数学
七年级
上册
教学重点:运用一元一次方程解决配套问题
创业几年荷包涨了,我得做点什么吧
对,可以给乡里的中学捐一些课桌吧
情景创设
老板,帮我做些课桌捐给乡里的中学吧,钱的事好说。
这是好事,可我只剩10立方米木材了,你要多少张课桌呀
情景创设
请问10立方米木材可以做多少张课桌呀
1立方米木材可以做50个桌面或300条桌腿;1个桌面配4条桌腿配套成1张课桌。你算算吧!
情景创设
学习目标
1.正确分析配套问题中的数量关系和数量相等关系,会运用一元一次方程解决配套问题.
2.掌握用一元一次方程解决实际问题的基本过程.
3.通过列方程解决实际问题的过程,体会建模思想.
一、复习与回顾
问题:之前我们通过列方程解应用问题的过程中,大致包含哪些步骤?
1.
审:审题,分析题目中的数量关系;
2.
设:设适当的未知数,并表示未知量;
3.
列:根据题目中的数量关系列方程;
4.
解:解这个方程;
6.
答:检验并作答
.
5.验:
检验所求解是否正确及是否符合题意;
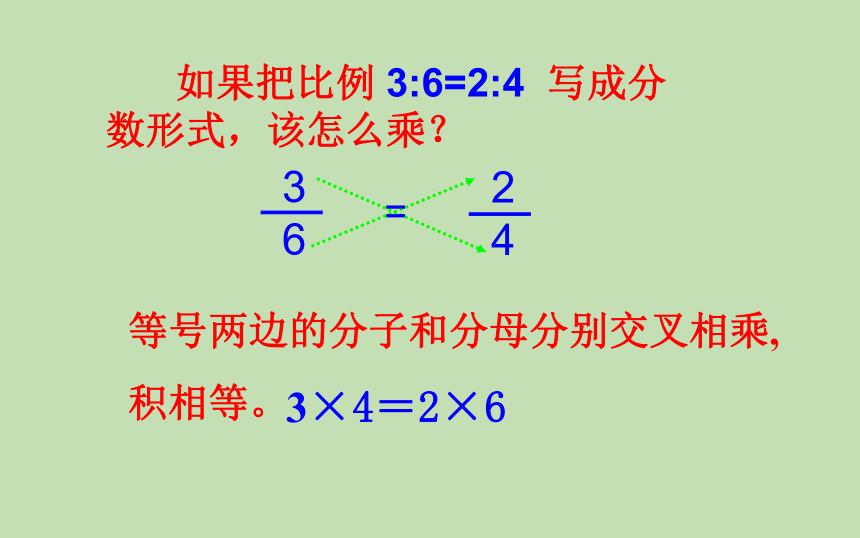
3×4=2×6
等号两边的分子和分母分别交叉相乘,
积相等。
如果把比例
3:6=2:4
写成分数形式,该怎么乘?
3
6
2
4
=
1个车身2个车轮
生活中的配套问题
1、一个自行车,由1个车身和2个车轮组成,则车身数和车轮数的比是
,如果要配套,车轮数量是车身数量的
倍。
等量关系:
车轮数量=2×车身数量
1:2
2
等量关系:
桌腿数量=4×桌面数量
2、一张方桌,由一个桌面和四条桌腿
组成,则桌面数和桌腿数的比是
,如果要配套,则桌腿数量是桌面数量的(
)倍
4
1:4
1个桌面4条腿
1、某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母.1个螺钉需要配
2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例题讲解
产品类型
生产人数
单人产量
总产量
螺钉
螺母
x
22-x
1200
2000
1200
x
2000(22-x)
解:设应安排x名工人生产螺钉,则安排(22-x)
人生产螺母.
螺钉总量:螺母总量=1:2
等量关系:螺母总量=2×螺钉总量
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
列方程
2
000(22-x)=2×1
200x
.
解方程,得
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
某水利工地派40人去挖土和运土,如果每人
每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?
设每天派x人挖土,则有
人运土,挖土数量:运土数量为
,可列方为
。
等量关系:挖土的数量
=
运土的数量
课堂训练
(40-x)
1:1
1立方米木材可以做50个桌面或300条桌腿;1张桌面配4条桌腿配套成1张课桌。你算算吧!
解:设用x立方米做桌面,则用(6-x)立方米做桌腿刚好配套.
产品类型
木材量
单位数量
总数量
桌面
桌腿
50
x
10-x
300(10-x)
解决问题
桌面数量:桌腿数量=1:4
怎样分配木材:多少立方米做桌面,多少立方米做桌腿,才能使桌面、桌腿刚好配套?
50
300
x
等量关系:桌腿数量=4×桌面数量
解:设用x立方米的木材做桌面,则用(10-x)立方米的木材做桌腿.
列方程,得300(10-x)=4×50x,
问题解决
x=6
10-x=4
可做方桌为50×6=300(张).
答:用6立方米的木材做桌面,4立方米的木材做桌腿,可做300张方桌.
1.现有工人34人,平均每人每天可加工大齿轮16个或小齿轮10个,又知3个大齿轮与4个小齿轮配成一套,要使每天生产的大小齿轮刚好配套,设有x个人生产大齿轮,则生产小齿轮的人有
人;生产大齿轮总数为
个,生产小齿轮总数为
个;大齿轮与小齿轮的数量比为
;可列方程为
。
牛刀小试:
(34-x)
3:4
16x
10(34-x)
30(34-x)=64x
2.某车间有26名工人,每人每天可以生产800个A部件或1000个B部件.
2个A部件需要配3个B部件,为使每天生产的A部件和B部件刚好配套,设安排x名工人生产A部件,则下面所列方程正确的是(
).
A.3×1000(26-x)=2×800x
B.1000(13-x)=800x
C2×1000(26-x)=3X800x
D.
1000(26-x)=800x
C
1.某服装厂要生产某种型号的秋装,已知2m长的某种布料可做衣身3个或衣袖5只,库内存这种布料132m,应如何分配布料生产衣身和衣袖才能恰好配套?
拓展提升
用布数量
单位产量
总产量
衣身
衣袖
x
衣身数量:衣袖数量=1:2
等量关系:衣袖数量=衣身数量×2
解:设做衣身用布料数量xm,则做衣袖用布料数量(132-x)m.
132-x
课堂训练
解:设生产衣身用布xm,则生产衣袖用布(132-x)m,依题意,得:
解得:
x=60
所以生产衣袖用布为:
132-x=72m
答:应该用60m的布料生产衣身,72m的布料生产衣袖.
2.七(14)班学生参加运土劳动,其中一部分人挑土,一部分人抬土,总共用40根扁担和60只筐.
问:有多少人抬土,多少人挑土?
解:设有x人抬土,则x人抬土用去
根扁担和
只筐;则挑土的人用去
根扁担和
只筐挑.
土所用的扁担:挑土所用的筐=
.
依题意得方程
.
解,得x=
.
故抬土的
人,挑土的有
人.
(40-x)
(60-x)
1:2
40
40
20
⑴
一般有两个未知量需要求出来,
可先设其一为x,
再用含x的代数式表示另一个未知量。
⑵
等量关系中的两个量往往其中一个量是另
一个量的培数或分数。
配套问题:
课堂小结
布置作业
课本106页2、3题
3.4.1实际问题与一元一次方程
——配套问题
人教版
数学
七年级
上册
教学重点:运用一元一次方程解决配套问题
创业几年荷包涨了,我得做点什么吧
对,可以给乡里的中学捐一些课桌吧
情景创设
老板,帮我做些课桌捐给乡里的中学吧,钱的事好说。
这是好事,可我只剩10立方米木材了,你要多少张课桌呀
情景创设
请问10立方米木材可以做多少张课桌呀
1立方米木材可以做50个桌面或300条桌腿;1个桌面配4条桌腿配套成1张课桌。你算算吧!
情景创设
学习目标
1.正确分析配套问题中的数量关系和数量相等关系,会运用一元一次方程解决配套问题.
2.掌握用一元一次方程解决实际问题的基本过程.
3.通过列方程解决实际问题的过程,体会建模思想.
一、复习与回顾
问题:之前我们通过列方程解应用问题的过程中,大致包含哪些步骤?
1.
审:审题,分析题目中的数量关系;
2.
设:设适当的未知数,并表示未知量;
3.
列:根据题目中的数量关系列方程;
4.
解:解这个方程;
6.
答:检验并作答
.
5.验:
检验所求解是否正确及是否符合题意;
3×4=2×6
等号两边的分子和分母分别交叉相乘,
积相等。
如果把比例
3:6=2:4
写成分数形式,该怎么乘?
3
6
2
4
=
1个车身2个车轮
生活中的配套问题
1、一个自行车,由1个车身和2个车轮组成,则车身数和车轮数的比是
,如果要配套,车轮数量是车身数量的
倍。
等量关系:
车轮数量=2×车身数量
1:2
2
等量关系:
桌腿数量=4×桌面数量
2、一张方桌,由一个桌面和四条桌腿
组成,则桌面数和桌腿数的比是
,如果要配套,则桌腿数量是桌面数量的(
)倍
4
1:4
1个桌面4条腿
1、某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母.1个螺钉需要配
2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例题讲解
产品类型
生产人数
单人产量
总产量
螺钉
螺母
x
22-x
1200
2000
1200
x
2000(22-x)
解:设应安排x名工人生产螺钉,则安排(22-x)
人生产螺母.
螺钉总量:螺母总量=1:2
等量关系:螺母总量=2×螺钉总量
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
列方程
2
000(22-x)=2×1
200x
.
解方程,得
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
某水利工地派40人去挖土和运土,如果每人
每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走?
设每天派x人挖土,则有
人运土,挖土数量:运土数量为
,可列方为
。
等量关系:挖土的数量
=
运土的数量
课堂训练
(40-x)
1:1
1立方米木材可以做50个桌面或300条桌腿;1张桌面配4条桌腿配套成1张课桌。你算算吧!
解:设用x立方米做桌面,则用(6-x)立方米做桌腿刚好配套.
产品类型
木材量
单位数量
总数量
桌面
桌腿
50
x
10-x
300(10-x)
解决问题
桌面数量:桌腿数量=1:4
怎样分配木材:多少立方米做桌面,多少立方米做桌腿,才能使桌面、桌腿刚好配套?
50
300
x
等量关系:桌腿数量=4×桌面数量
解:设用x立方米的木材做桌面,则用(10-x)立方米的木材做桌腿.
列方程,得300(10-x)=4×50x,
问题解决
x=6
10-x=4
可做方桌为50×6=300(张).
答:用6立方米的木材做桌面,4立方米的木材做桌腿,可做300张方桌.
1.现有工人34人,平均每人每天可加工大齿轮16个或小齿轮10个,又知3个大齿轮与4个小齿轮配成一套,要使每天生产的大小齿轮刚好配套,设有x个人生产大齿轮,则生产小齿轮的人有
人;生产大齿轮总数为
个,生产小齿轮总数为
个;大齿轮与小齿轮的数量比为
;可列方程为
。
牛刀小试:
(34-x)
3:4
16x
10(34-x)
30(34-x)=64x
2.某车间有26名工人,每人每天可以生产800个A部件或1000个B部件.
2个A部件需要配3个B部件,为使每天生产的A部件和B部件刚好配套,设安排x名工人生产A部件,则下面所列方程正确的是(
).
A.3×1000(26-x)=2×800x
B.1000(13-x)=800x
C2×1000(26-x)=3X800x
D.
1000(26-x)=800x
C
1.某服装厂要生产某种型号的秋装,已知2m长的某种布料可做衣身3个或衣袖5只,库内存这种布料132m,应如何分配布料生产衣身和衣袖才能恰好配套?
拓展提升
用布数量
单位产量
总产量
衣身
衣袖
x
衣身数量:衣袖数量=1:2
等量关系:衣袖数量=衣身数量×2
解:设做衣身用布料数量xm,则做衣袖用布料数量(132-x)m.
132-x
课堂训练
解:设生产衣身用布xm,则生产衣袖用布(132-x)m,依题意,得:
解得:
x=60
所以生产衣袖用布为:
132-x=72m
答:应该用60m的布料生产衣身,72m的布料生产衣袖.
2.七(14)班学生参加运土劳动,其中一部分人挑土,一部分人抬土,总共用40根扁担和60只筐.
问:有多少人抬土,多少人挑土?
解:设有x人抬土,则x人抬土用去
根扁担和
只筐;则挑土的人用去
根扁担和
只筐挑.
土所用的扁担:挑土所用的筐=
.
依题意得方程
.
解,得x=
.
故抬土的
人,挑土的有
人.
(40-x)
(60-x)
1:2
40
40
20
⑴
一般有两个未知量需要求出来,
可先设其一为x,
再用含x的代数式表示另一个未知量。
⑵
等量关系中的两个量往往其中一个量是另
一个量的培数或分数。
配套问题:
课堂小结
布置作业
课本106页2、3题
