人教版数学八 年级上册14.1.1同底数幂的乘法课件(16张)
文档属性
| 名称 | 人教版数学八 年级上册14.1.1同底数幂的乘法课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 143.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 13:39:28 | ||
图片预览






文档简介
(共16张PPT)
14.1.1同底数幂的乘法
a
n
指数
幂
=
a·a·
…
·a
n个a相乘
底数
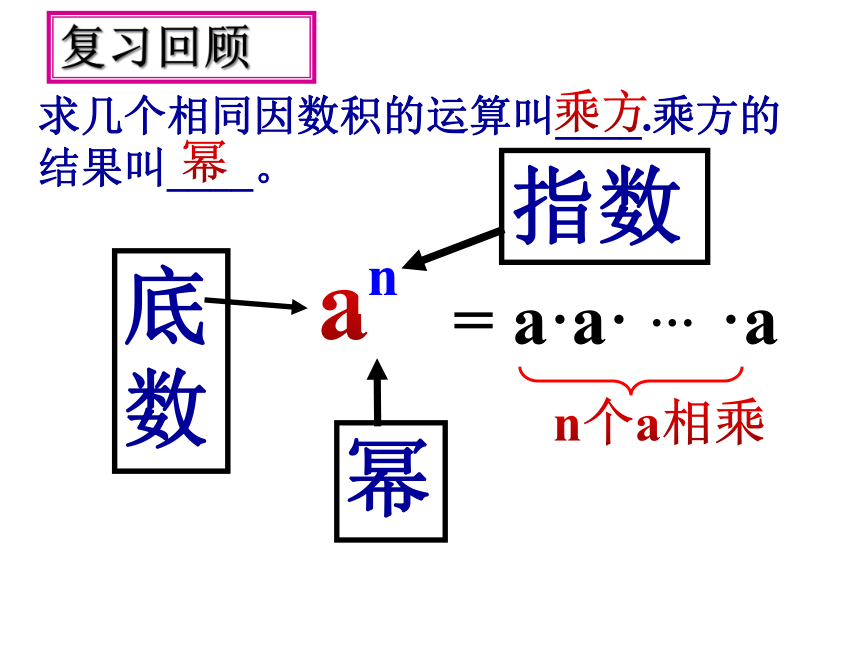
求几个相同因数积的运算叫____.乘方的结果叫____。
乘方
复习回顾
幂
(1)2
表示_____________;
5
(2)10×10×10×10可以写成____;
(3)
a的底数是__,指数是__;
(4)(a+b)
的底数是___,指数是__;
3
(5)(-2)
的底数是___,指数是__;
4
(6)
-2
的底数是___,指数是__.
4
2×2×2×2×2
10
4
a
1
a+b
3
-2
4
2
4
热身训练
某种电子计算机每秒可进行1千万亿(1015)次运算,它工作103
s可进行多少次运算?
(1)你会根据题意列出算式吗?
(2)1015的意义是什么?103
呢?
(3)你知道怎样计算吗?
新课引入
25
×
22
a3
·
a2
5m
×
5n
=27
=a5
探索新知
根据乘方的意义填空:
(1)上述三组乘法运算的乘数各有什么共同特征?
(2)它们的积都是什么形式?积的各个部分与它的乘
数有什么关系?
(3)
根据你的观察,你能再举个例子,使它具有上述
特征吗?同桌交流。
=5(m+n)
你能将上面发现的规律推导出来吗?
am
·
an
(m,n都是正整数)
探索新知
am
·
an
=am+n
(m,n都是正整数)
通过上面的探索和推导,你能用文字语言概括出同底数幂的乘法的运算性质吗?
同底数幂相乘,底数不变,指数相加。
探索新知
运用新知
判断下列计算是否正确,并说明理由:
(1)
(2)
(3)
(4)
(5)
例1、计算:
(1)
(2)
(3)
运用新知
(4)
=a·a·
…
·a
(m+n+p)个a相乘
=am+n+p
am
·
an
·
ap
=(a·a·
…
·a)(a·a·
…
·a)(a·a·
···
·a)
m个a
n个a
p个a
拓广延伸
计算:(1)
(-3)
·
34
·
(-3)3
解:原式=
=(-3)1+4+3
=(-3)8
=38
(-3)
·(-3)4
·
(-3)3
拓广探索
(2)
(x+y)3
·
(x+y)4
.
解:
原式
am
·
an
=
am+n
公式中的a可代表单项式,也可以代表多项式.
=(x+y)3+4
=(x+y)7
拓广探索
小试牛刀
1、计算:
(1)(-x)·
(-x)3
(2)(m-n)·
(n-m)4·
(m-n)7
(3)-a2
·
a6
;
2、填空:(1)x5
·(
)=x
8
(2)xm
·
(
)=x3m
x3
x2m
1.已知:a5=7;a3=16.则a8=(
)
2.已知2m=a,2n=b,(m,n都是正整数).则2m+n=(
)
3.计算:
(-2)2006
-
22007
大显身手
(1)本节课主要学习了哪些内容?你有什么收获呢?
(2)同底数幂的乘法的运算性质是怎么探究并推导出
来的?
(3)在运用同底数幂的乘法的运算性质时要注意什么?
课堂小结
(1)同底数幂的乘法运算性质。
(2)探究推导的过程注重渗透了从特殊到一般、从具体到抽象的数学思想方法。
(3)运用时的注意事项:
①同底
②乘法运算
③底数、指数均可为多项式
④注意符号问题
课堂小结
14.1.1同底数幂的乘法
a
n
指数
幂
=
a·a·
…
·a
n个a相乘
底数
求几个相同因数积的运算叫____.乘方的结果叫____。
乘方
复习回顾
幂
(1)2
表示_____________;
5
(2)10×10×10×10可以写成____;
(3)
a的底数是__,指数是__;
(4)(a+b)
的底数是___,指数是__;
3
(5)(-2)
的底数是___,指数是__;
4
(6)
-2
的底数是___,指数是__.
4
2×2×2×2×2
10
4
a
1
a+b
3
-2
4
2
4
热身训练
某种电子计算机每秒可进行1千万亿(1015)次运算,它工作103
s可进行多少次运算?
(1)你会根据题意列出算式吗?
(2)1015的意义是什么?103
呢?
(3)你知道怎样计算吗?
新课引入
25
×
22
a3
·
a2
5m
×
5n
=27
=a5
探索新知
根据乘方的意义填空:
(1)上述三组乘法运算的乘数各有什么共同特征?
(2)它们的积都是什么形式?积的各个部分与它的乘
数有什么关系?
(3)
根据你的观察,你能再举个例子,使它具有上述
特征吗?同桌交流。
=5(m+n)
你能将上面发现的规律推导出来吗?
am
·
an
(m,n都是正整数)
探索新知
am
·
an
=am+n
(m,n都是正整数)
通过上面的探索和推导,你能用文字语言概括出同底数幂的乘法的运算性质吗?
同底数幂相乘,底数不变,指数相加。
探索新知
运用新知
判断下列计算是否正确,并说明理由:
(1)
(2)
(3)
(4)
(5)
例1、计算:
(1)
(2)
(3)
运用新知
(4)
=a·a·
…
·a
(m+n+p)个a相乘
=am+n+p
am
·
an
·
ap
=(a·a·
…
·a)(a·a·
…
·a)(a·a·
···
·a)
m个a
n个a
p个a
拓广延伸
计算:(1)
(-3)
·
34
·
(-3)3
解:原式=
=(-3)1+4+3
=(-3)8
=38
(-3)
·(-3)4
·
(-3)3
拓广探索
(2)
(x+y)3
·
(x+y)4
.
解:
原式
am
·
an
=
am+n
公式中的a可代表单项式,也可以代表多项式.
=(x+y)3+4
=(x+y)7
拓广探索
小试牛刀
1、计算:
(1)(-x)·
(-x)3
(2)(m-n)·
(n-m)4·
(m-n)7
(3)-a2
·
a6
;
2、填空:(1)x5
·(
)=x
8
(2)xm
·
(
)=x3m
x3
x2m
1.已知:a5=7;a3=16.则a8=(
)
2.已知2m=a,2n=b,(m,n都是正整数).则2m+n=(
)
3.计算:
(-2)2006
-
22007
大显身手
(1)本节课主要学习了哪些内容?你有什么收获呢?
(2)同底数幂的乘法的运算性质是怎么探究并推导出
来的?
(3)在运用同底数幂的乘法的运算性质时要注意什么?
课堂小结
(1)同底数幂的乘法运算性质。
(2)探究推导的过程注重渗透了从特殊到一般、从具体到抽象的数学思想方法。
(3)运用时的注意事项:
①同底
②乘法运算
③底数、指数均可为多项式
④注意符号问题
课堂小结
