沪科版(2012)初中数学九年级上册 23.2.1 解直角三角形及其应用教案
文档属性
| 名称 | 沪科版(2012)初中数学九年级上册 23.2.1 解直角三角形及其应用教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1001.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 13:48:30 | ||
图片预览


文档简介
九年级数学备课表
课题名称
23.2.2解直角三角形及其应用
学情分析
直角三角形是最简单、最基本的几何图形,在生活中随处可见,是研究其他图形的基础,在解决实际问题中也有着广泛的应用.渗透着数形结合思想、方程思想、转化思想。因此本课无论是在本章还是在整个初中数学教材中都具有重要的地位。对于九年级学生,从人的认知规律看,他们已经具有初步的探究能力和逻辑思维能力。但直角三角形的应用题型较多,他们对建立直角三角形模型上可能会有困难。
教学目标
知识与技能:使学生掌握仰角、俯角的概念,并学会正确地运用这些概念和解直角三角形的知识解决一些实际问题.
过程与方法:利用“割补法”转化图形,让学生体验转化思想、方程思想和数形结合思想在解直角三角形中的用途.
情感态度与价值观:使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
教学重点
将实际问题转化为解直角三角形问题.
教学难点
将实际问题中的数量关系如何转化为直角三角形中元素间的关系求解.
教学准备
课件,课前预习
教学课时
1课时
教学过程
幻灯片
一、感知生活,快乐起航
师:请同学们欣赏一组图片,这是我校周一进行升旗仪式时拍摄的一组图片,看五星红旗迎风飘扬,这里的“看”,从数学的角度来说属于什么?
生:仰视.
归纳:在进行观察或测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
师:想知道我们学校旗杆的高度,你们有什么办法?
生:问询负责人、利用相似(影长)、测量国旗绳长(标记号)、利用三角函数等.
师:现在我们就一起研究利用直角三角形来解决这类问题.
二、合作交流,探索新知
(一)五星红旗
迎风飘扬
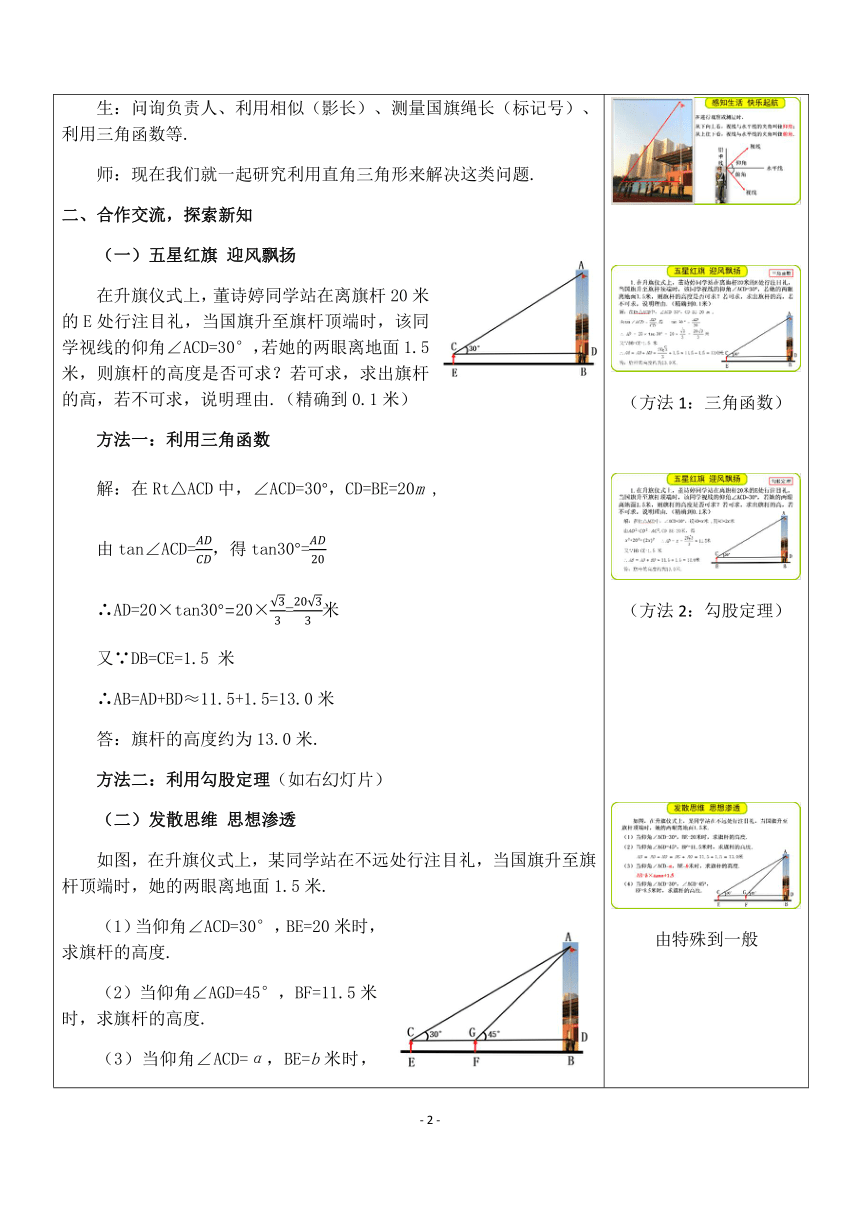
在升旗仪式上,董诗婷同学站在离旗杆20米的E处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角∠ACD=30°,若她的两眼离地面1.5米,则旗杆的高度是否可求?若可求,求出旗杆的高,若不可求,说明理由.(精确到0.1米)
方法一:利用三角函数
解:在Rt△ACD中,∠ACD=30°,CD=BE=20m
,
由tan∠ACD=,得tan30°=
∴AD=20×tan30°=20×=米
又∵DB=CE=1.5
米
∴AB=AD+BD≈11.5+1.5=13.0米
答:旗杆的高度约为13.0米.
方法二:利用勾股定理(如右幻灯片)
(二)发散思维
思想渗透
如图,在升旗仪式上,某同学站在不远处行注目礼,当国旗升至旗杆顶端时,她的两眼离地面1.5米.
(1)当仰角∠ACD=30°,BE=20米时,求旗杆的高度.
(2)当仰角∠AGD=45°,BF=11.5米时,求旗杆的高度.
(3)当仰角∠ACD=α,BE=b米时,求旗杆的高度.
(4)当仰角∠ACD=30°,∠AGD=45°,EF=8.5米时,求旗杆的高度.
三、例题学习,承上启下
(1)数形结合
一题多解
如图,在测量旗杆的高度AB时,董诗婷同学从与旗杆底成一条直线的地面上E、F两处,测得视线的仰角分别为30°和45°,这两个观测点之间的水平距离EF为8.5米,她的两眼离地面1.5米.根据这些数据,你能求得旗杆的高度吗?(精确到0.1米)
方法一:利用三角函数
解:设AD=x
米,在Rt△AGD中,∵∠AGD=45°,
∴GD=AD=x
米,
CD=(8.5+x
)米
在Rt△ACD中,∵∠ACD=30°
∴AD=x≈11.6
米
∵DB=CE=1.5米
答:旗杆的高度约为13.1米.
方法二:利用勾股定理
方法三:三角函数与勾股定理相结合
一般用来计算底部不能直接到达的物体的高度.
(2)海中遨游
安全第一
如图,一船以20
n
mile/h的速度向东航行,在A处测得灯塔C在北偏东60°的方向上,继续航行1h到达B处,再测得灯塔C在北偏东30°的方向上.已知灯塔C四周10
n
mile内有暗礁,问这船继续向东航行是否安全?
考查三角函数知识的应用和“垂线短最短”的复习回顾,从图形上来说是利用了割补法当中的“补”来解决几何问题。
方法一:利用三角函数
方法二:利用等腰三角形的判定和勾股定理
四、随堂练习,巩固新知
(一)空中飞舞
或割或补
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果保留根号)
2.如图,某直升机于空中A处测得正前方地面控制点C的俯角为30°;若航向不变,直升机继续向前飞行1000米至B处,测得地面控制点C的俯角为45°.求直升机再向前飞行多远,与地面控制点C的距离最近.
(二)中考真题
实战演练
1.如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600米,α=75°,β=45°,求DE的长.(参考数据:sin75°≈0.97,cos75°≈0.26,)
2017年安徽中考第17题
2018年安徽中考第19题
2.为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B、E、D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为
45°,FD=1.8米,问旗杆AB的高度约为多少米?
(结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)
课堂总结,提炼升华
回顾课堂
归纳模式
(二)梳理思路
思想渗透
利用解直角三角形的知识解决实际问题的一般过程是:
1.将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案
得到实际问题的答案.
数学思想方法:转化思想、数形结合思想、方程思想、割补法等.
六、作业设置,课外延伸
习题23.2第3、4题
(方法1:三角函数)
(方法2:勾股定理)
由特殊到一般
方法1:先45°后30°
方法2:先30°后45°
方法3:勾股定理
利用割补法,利用三角函数或勾股定理解决问题.
空中飞舞
或割或补
通过2017年和2018年相关中考真题训练,让学生真切感受中考,提前进行实战演练.
归纳利用直角三角形解应用题的几种常见模式,让学生进行归纳对比,能够举一反三,灵活运用.
梳理思路
渗透思想方法
板书设计
23.2
解直角三角形
一、将实际问题抽象为数学问题
二、解直角三角形;
三、数学问题的答案——实际问题的答案.
四、数学思想方法
教学反思
-
1
-
课题名称
23.2.2解直角三角形及其应用
学情分析
直角三角形是最简单、最基本的几何图形,在生活中随处可见,是研究其他图形的基础,在解决实际问题中也有着广泛的应用.渗透着数形结合思想、方程思想、转化思想。因此本课无论是在本章还是在整个初中数学教材中都具有重要的地位。对于九年级学生,从人的认知规律看,他们已经具有初步的探究能力和逻辑思维能力。但直角三角形的应用题型较多,他们对建立直角三角形模型上可能会有困难。
教学目标
知识与技能:使学生掌握仰角、俯角的概念,并学会正确地运用这些概念和解直角三角形的知识解决一些实际问题.
过程与方法:利用“割补法”转化图形,让学生体验转化思想、方程思想和数形结合思想在解直角三角形中的用途.
情感态度与价值观:使学生感知本节课与现实生活的密切联系,进一步认识到将数学知识运用于实践的意义.
教学重点
将实际问题转化为解直角三角形问题.
教学难点
将实际问题中的数量关系如何转化为直角三角形中元素间的关系求解.
教学准备
课件,课前预习
教学课时
1课时
教学过程
幻灯片
一、感知生活,快乐起航
师:请同学们欣赏一组图片,这是我校周一进行升旗仪式时拍摄的一组图片,看五星红旗迎风飘扬,这里的“看”,从数学的角度来说属于什么?
生:仰视.
归纳:在进行观察或测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
师:想知道我们学校旗杆的高度,你们有什么办法?
生:问询负责人、利用相似(影长)、测量国旗绳长(标记号)、利用三角函数等.
师:现在我们就一起研究利用直角三角形来解决这类问题.
二、合作交流,探索新知
(一)五星红旗
迎风飘扬
在升旗仪式上,董诗婷同学站在离旗杆20米的E处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角∠ACD=30°,若她的两眼离地面1.5米,则旗杆的高度是否可求?若可求,求出旗杆的高,若不可求,说明理由.(精确到0.1米)
方法一:利用三角函数
解:在Rt△ACD中,∠ACD=30°,CD=BE=20m
,
由tan∠ACD=,得tan30°=
∴AD=20×tan30°=20×=米
又∵DB=CE=1.5
米
∴AB=AD+BD≈11.5+1.5=13.0米
答:旗杆的高度约为13.0米.
方法二:利用勾股定理(如右幻灯片)
(二)发散思维
思想渗透
如图,在升旗仪式上,某同学站在不远处行注目礼,当国旗升至旗杆顶端时,她的两眼离地面1.5米.
(1)当仰角∠ACD=30°,BE=20米时,求旗杆的高度.
(2)当仰角∠AGD=45°,BF=11.5米时,求旗杆的高度.
(3)当仰角∠ACD=α,BE=b米时,求旗杆的高度.
(4)当仰角∠ACD=30°,∠AGD=45°,EF=8.5米时,求旗杆的高度.
三、例题学习,承上启下
(1)数形结合
一题多解
如图,在测量旗杆的高度AB时,董诗婷同学从与旗杆底成一条直线的地面上E、F两处,测得视线的仰角分别为30°和45°,这两个观测点之间的水平距离EF为8.5米,她的两眼离地面1.5米.根据这些数据,你能求得旗杆的高度吗?(精确到0.1米)
方法一:利用三角函数
解:设AD=x
米,在Rt△AGD中,∵∠AGD=45°,
∴GD=AD=x
米,
CD=(8.5+x
)米
在Rt△ACD中,∵∠ACD=30°
∴AD=x≈11.6
米
∵DB=CE=1.5米
答:旗杆的高度约为13.1米.
方法二:利用勾股定理
方法三:三角函数与勾股定理相结合
一般用来计算底部不能直接到达的物体的高度.
(2)海中遨游
安全第一
如图,一船以20
n
mile/h的速度向东航行,在A处测得灯塔C在北偏东60°的方向上,继续航行1h到达B处,再测得灯塔C在北偏东30°的方向上.已知灯塔C四周10
n
mile内有暗礁,问这船继续向东航行是否安全?
考查三角函数知识的应用和“垂线短最短”的复习回顾,从图形上来说是利用了割补法当中的“补”来解决几何问题。
方法一:利用三角函数
方法二:利用等腰三角形的判定和勾股定理
四、随堂练习,巩固新知
(一)空中飞舞
或割或补
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果保留根号)
2.如图,某直升机于空中A处测得正前方地面控制点C的俯角为30°;若航向不变,直升机继续向前飞行1000米至B处,测得地面控制点C的俯角为45°.求直升机再向前飞行多远,与地面控制点C的距离最近.
(二)中考真题
实战演练
1.如图,游客在点A处坐缆车出发,沿A-B-D的路线可至山顶D处,假设AB和BD都是直线段,且AB=BD=600米,α=75°,β=45°,求DE的长.(参考数据:sin75°≈0.97,cos75°≈0.26,)
2017年安徽中考第17题
2018年安徽中考第19题
2.为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B、E、D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为
45°,FD=1.8米,问旗杆AB的高度约为多少米?
(结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)
课堂总结,提炼升华
回顾课堂
归纳模式
(二)梳理思路
思想渗透
利用解直角三角形的知识解决实际问题的一般过程是:
1.将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案
得到实际问题的答案.
数学思想方法:转化思想、数形结合思想、方程思想、割补法等.
六、作业设置,课外延伸
习题23.2第3、4题
(方法1:三角函数)
(方法2:勾股定理)
由特殊到一般
方法1:先45°后30°
方法2:先30°后45°
方法3:勾股定理
利用割补法,利用三角函数或勾股定理解决问题.
空中飞舞
或割或补
通过2017年和2018年相关中考真题训练,让学生真切感受中考,提前进行实战演练.
归纳利用直角三角形解应用题的几种常见模式,让学生进行归纳对比,能够举一反三,灵活运用.
梳理思路
渗透思想方法
板书设计
23.2
解直角三角形
一、将实际问题抽象为数学问题
二、解直角三角形;
三、数学问题的答案——实际问题的答案.
四、数学思想方法
教学反思
-
1
-
