沪科版(2012)数学九年级上册23.1.1锐角的三角函数 课件(23张PPT)
文档属性
| 名称 | 沪科版(2012)数学九年级上册23.1.1锐角的三角函数 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 139.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
23.1.1锐角的三角函数
情景引入
(1)生活中大家经常听到“某山坡比较陡”
“坡度大”“坡角比较大”这些话,怎样
描述坡面的坡度(倾斜程度)呢?
(2)在直角三角形中,知道一边和一锐角,
你能求出其他的边和角吗?
通过本章的学习,相信大家一定
能够解决这些问题,这节课我们先从
坡面倾斜程度谈起。
新课讲解
(1)如图,有两个直角三角形,直角边
AB和DF表示水平面,斜边AC和EF分别
表示两个不同的坡面,坡面AC和EF那个
更陡?你是怎么判断的?
(AB=DF)
A
C
B
F
E
D
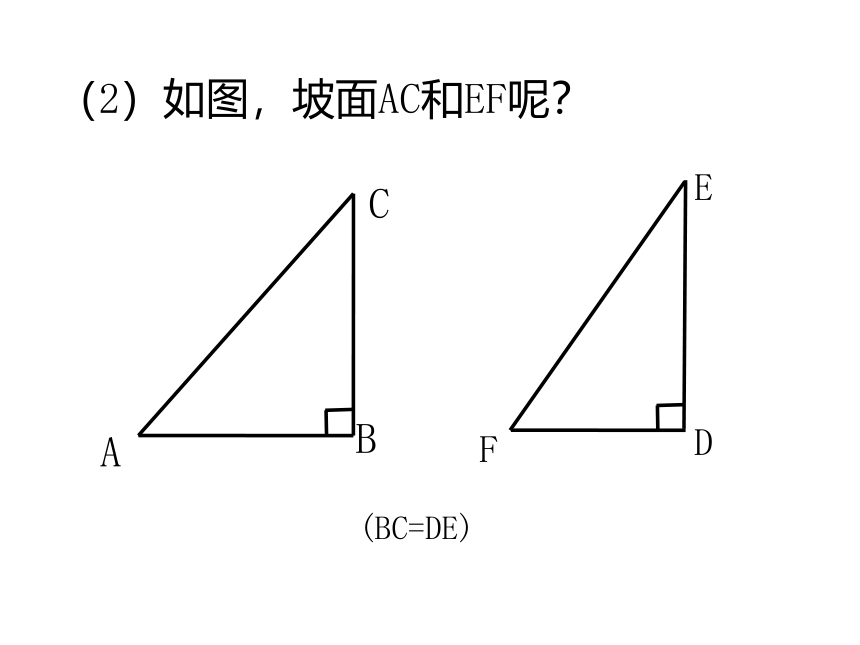
(2)如图,坡面AC和EF呢?
(BC=DE)
A
C
B
F
E
D
(3)坡面AC和EF那个更陡?
你是怎样判断的?
(AB=FD
BC=DE)
A
C
B
E
D
F
(4)动手操作:
如图,在锐角的一边上任取一点B,自点B
向另一边作垂线,垂足为C,测量BC、AC
并计算
的值;再取一点D,测量DE、AE
并计算
?为什么?
B
C
E
D
A
l
m
●
●
演示
α
动手实践,寻找规律
A
B
C
B’
C’
由推理可得:角度不变,比值不变
由动态演示:角度改变,比值改变
β
D
D’
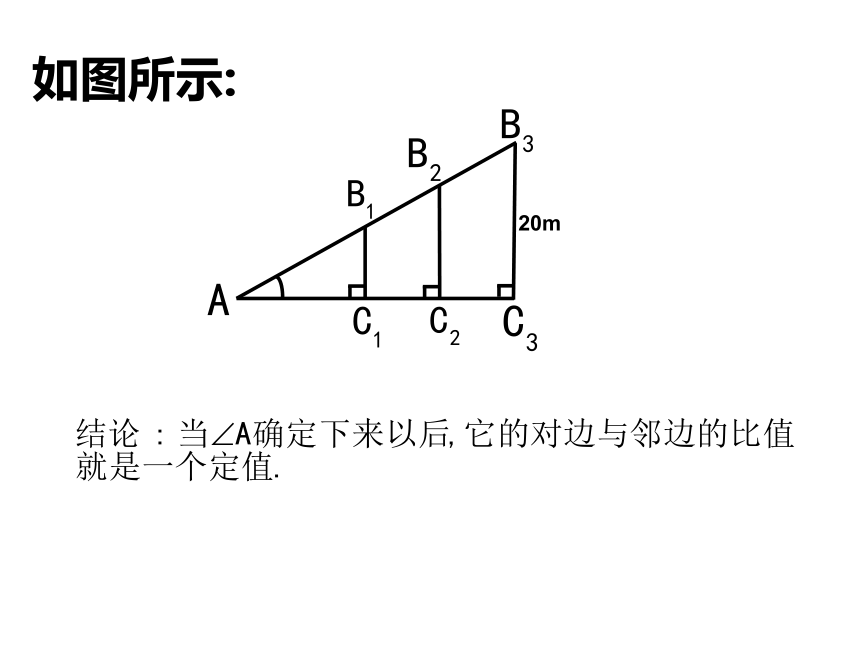
如图所示:
20m
由于Rt△ABC直角三角形中锐角A确定以后,
它的对边和邻边的比值也随之确定,因此我
们有如下定义:
在Rt△ABC中,我们把锐角A的对边和邻边
的比叫做∠A的正切,记作tanA,如图:
A
C
B
c
a
b
1.
tanA是一个完整的符号,tanA不表示“tan”
乘以“∠A”。
2.
它表示∠A的正切,记号里习惯省去角的
符号“∠”
3
.tanA没有单位,它表示一个比值,锐角A
的对边和邻边的比。
4.初中阶段仅研究直角三角形中,是锐角的
正切,将来遇到正切问题,也必须放在直
角三角形中去研究。
∠B的正切如何表示呢?它的数学意义如何?
C
A
B
c
a
b
那么,现在我们再回到本节开始问题中来,
如何来描述坡面的坡度呢?
可以用正切来描述
我们可以用正切来描述坡面的坡度,坡面的
铅直高度h和水平长度l的比叫做坡度(或坡比)
记作i,即:
坡面和水平面的夹角叫做坡角,于是有:
显然坡度(i=tanα)越大坡角越大,坡越陡
l
h
i=h:l
如:有一山坡在水平方向上每前进100m就升高
60m,那么此山坡的坡度是多少?
在实际生活中,我们常常也用倾斜角来描述斜坡面陡的程度。如一个梯子靠在墙上陡的程度,电线杆的倾斜等等,但是对于公路坡面陡的程度,就不能直接测到公路路面的倾斜角,只有用坡比,也就是倾斜角的正切值。以后在测量山高,大楼的高度等也都要用到正切知识。
例题解析
例1:在Rt△ABC中,∠C=90°,BC=3cm,
AC=4cm.求tanA和tanB
B
C
A
例题解析
例2:在Rt△ABC中,∠C=90°,BC=12cm,
AB=20cm.求tanA和tanB
B
C
A
解:
例3:在Rt△ABC中,∠C=90°,AC+BC=7
(AC>BC),AB=5.求tanB
例题解析
B
C
A
例题解析
例4:在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
,
求tan∠BCD.
B
C
A
D
解:∵
练习
1:在Rt△ABC中,∠C=90°,AC=12,
,求BC的长。
B
C
A
2.如图,汽车从引桥下端点A行驶200m后到达
高架桥的点B,已知高架桥的垂直高度BC
为12m,求引桥的坡度(精确到0.01)。
A
B
C
小结
本节课从坡面的倾斜角度谈起,经历了探
索直角三角形中的边角关系,得出直角三角形
中锐角确定之后,它的对边与邻边的比也随之
确定,并以此为基础,在直角三角形中
定义:
接着,了解了坡面的倾斜程度与正切的关系,
tanα的值越大,坡面越陡.
布置作业:
23.1.1锐角的三角函数
情景引入
(1)生活中大家经常听到“某山坡比较陡”
“坡度大”“坡角比较大”这些话,怎样
描述坡面的坡度(倾斜程度)呢?
(2)在直角三角形中,知道一边和一锐角,
你能求出其他的边和角吗?
通过本章的学习,相信大家一定
能够解决这些问题,这节课我们先从
坡面倾斜程度谈起。
新课讲解
(1)如图,有两个直角三角形,直角边
AB和DF表示水平面,斜边AC和EF分别
表示两个不同的坡面,坡面AC和EF那个
更陡?你是怎么判断的?
(AB=DF)
A
C
B
F
E
D
(2)如图,坡面AC和EF呢?
(BC=DE)
A
C
B
F
E
D
(3)坡面AC和EF那个更陡?
你是怎样判断的?
(AB=FD
BC=DE)
A
C
B
E
D
F
(4)动手操作:
如图,在锐角的一边上任取一点B,自点B
向另一边作垂线,垂足为C,测量BC、AC
并计算
的值;再取一点D,测量DE、AE
并计算
?为什么?
B
C
E
D
A
l
m
●
●
演示
α
动手实践,寻找规律
A
B
C
B’
C’
由推理可得:角度不变,比值不变
由动态演示:角度改变,比值改变
β
D
D’
如图所示:
20m
由于Rt△ABC直角三角形中锐角A确定以后,
它的对边和邻边的比值也随之确定,因此我
们有如下定义:
在Rt△ABC中,我们把锐角A的对边和邻边
的比叫做∠A的正切,记作tanA,如图:
A
C
B
c
a
b
1.
tanA是一个完整的符号,tanA不表示“tan”
乘以“∠A”。
2.
它表示∠A的正切,记号里习惯省去角的
符号“∠”
3
.tanA没有单位,它表示一个比值,锐角A
的对边和邻边的比。
4.初中阶段仅研究直角三角形中,是锐角的
正切,将来遇到正切问题,也必须放在直
角三角形中去研究。
∠B的正切如何表示呢?它的数学意义如何?
C
A
B
c
a
b
那么,现在我们再回到本节开始问题中来,
如何来描述坡面的坡度呢?
可以用正切来描述
我们可以用正切来描述坡面的坡度,坡面的
铅直高度h和水平长度l的比叫做坡度(或坡比)
记作i,即:
坡面和水平面的夹角叫做坡角,于是有:
显然坡度(i=tanα)越大坡角越大,坡越陡
l
h
i=h:l
如:有一山坡在水平方向上每前进100m就升高
60m,那么此山坡的坡度是多少?
在实际生活中,我们常常也用倾斜角来描述斜坡面陡的程度。如一个梯子靠在墙上陡的程度,电线杆的倾斜等等,但是对于公路坡面陡的程度,就不能直接测到公路路面的倾斜角,只有用坡比,也就是倾斜角的正切值。以后在测量山高,大楼的高度等也都要用到正切知识。
例题解析
例1:在Rt△ABC中,∠C=90°,BC=3cm,
AC=4cm.求tanA和tanB
B
C
A
例题解析
例2:在Rt△ABC中,∠C=90°,BC=12cm,
AB=20cm.求tanA和tanB
B
C
A
解:
例3:在Rt△ABC中,∠C=90°,AC+BC=7
(AC>BC),AB=5.求tanB
例题解析
B
C
A
例题解析
例4:在Rt△ABC中,∠ACB=90°,CD⊥AB于D.
,
求tan∠BCD.
B
C
A
D
解:∵
练习
1:在Rt△ABC中,∠C=90°,AC=12,
,求BC的长。
B
C
A
2.如图,汽车从引桥下端点A行驶200m后到达
高架桥的点B,已知高架桥的垂直高度BC
为12m,求引桥的坡度(精确到0.01)。
A
B
C
小结
本节课从坡面的倾斜角度谈起,经历了探
索直角三角形中的边角关系,得出直角三角形
中锐角确定之后,它的对边与邻边的比也随之
确定,并以此为基础,在直角三角形中
定义:
接着,了解了坡面的倾斜程度与正切的关系,
tanα的值越大,坡面越陡.
布置作业:
