冀教版初中数学七年级上册 1.3 绝对值和相反数 课件(37张)
文档属性
| 名称 | 冀教版初中数学七年级上册 1.3 绝对值和相反数 课件(37张) |

|
|
| 格式 | zip | ||
| 文件大小 | 504.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 13:54:56 | ||
图片预览










文档简介
(共37张PPT)
数轴
绝对值与相反数
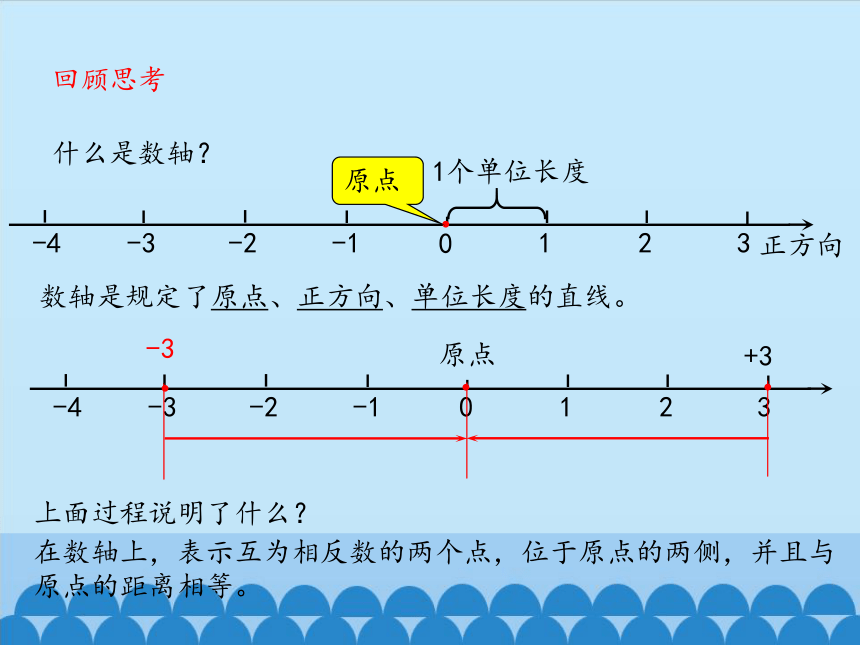
什么是数轴?
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
数轴是规定了原点、正方向、单位长度的直线。
上面过程说明了什么?
0
-4
-3
-2
-1
3
2
1
-3
+3
原点
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点的距离相等。
回顾思考
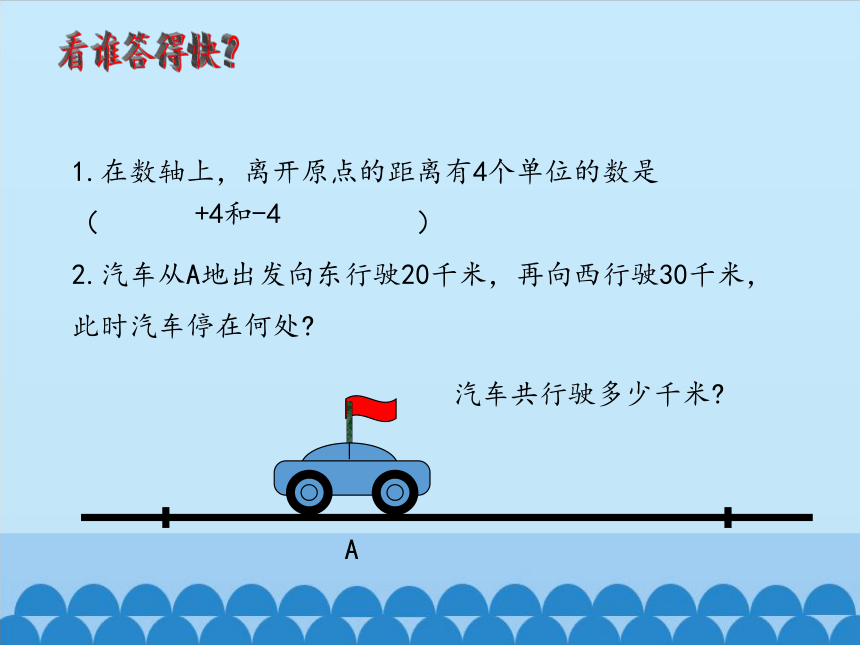
看谁答得快?
1.在数轴上,离开原点的距离有4个单位的数是(
)
2.汽车从A地出发向东行驶20千米,再向西行驶30千米,此时汽车停在何处?
+4和-4
汽车共行驶多少千米?
A
创设问题情境
1、两只小狗从同一点0出发,在一条笔直的街上跑,一只向右跑3米到达A点,另一只向左跑3米到达B点。若规定向右为正,则A处记做_______,B处记做_______。
2、这两只小狗在跑的过程中,有没有共同的地方?在数轴上的A、B两点又有什么特征?
A
B
小
结:
在实际生活中,有时存在这样的情况,无需考虑数的正负性质,比如:在计算小狗所跑的路程中,与小狗跑的方向无关,这时所走的路程只需用正数,这样就引进了一个新的概念———绝对值。
绝对值:一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
∵
-5到原点的距离是5,
∴
-5的绝对值是5,记|-5|=5;
又:5的绝对值是5,记做|5|=5。
注意:①与原点的关系
②是一个距离的概念
规定
绝对值的几何定义:
例1:求下列各数的绝对值:
解:
应用深化知识
请你举出一些相反数的例子
像3和-3,5和-5等这样符号不同,绝对值相等的数,我们称其中一个是另外一个数的相反数,也称这两个数互为相反数。0的相反数规定为0。
特点:
1、一个正数的绝对值是它本身;
2、一个负数的绝对值是它的相反数;
3、零的绝对值是零;
4、互为相反数的两个数的绝对值相等。
|
5
-
1
|
=
(
)
1
+
|
-5
|
=(
)
|
5
|
-
|
-3
|
=(
)
|
-1
|
×
|
-2
|
=(
)
|
-6.2
|
÷
|
+2
|
=(
)
填一填
分析:先求算式中绝对值的值,然后进行四则运算。
(1)一个数的绝对值一定是正数。
(
)
(2)一个数的绝对值不可能是负数。
(
)
(3)互为相反数的两个数,它们的绝对值一定相等。(
)
(4)绝对值是同一个正数的数有两个,且它们是互为相反数。
(
)
探索挑战
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
问题1:字母a表示一个数,-a表示什么?-a一定是负数吗?
问题2:如果数a的绝对值等于a,那么a可能是正数吗?可能是负数吗?可能是零吗?
问题3:如果数a的绝对值等于-a,那么a可能是正数吗?可能是负数吗?可能是零吗?
归纳:
1.绝对值的定义;
2.绝对值的性质:
(1)正数的绝对值是它本身;
(2)负数的绝对值是它的相反数;
(3)0的绝对值是0;
(4)互为相反数的两个数的绝对值相等。
归纳小结反思
练习:回答下列问题
①一个数的绝对值是它本身,这个数是什么数?
②一个数的绝对值是它的相反数,这个数是什么数?
③一个数的绝对值一定是正数吗?
④一个数的绝对值不可能是负数,对吗?
(正数和零)
(负数和零)
(不一定)
(对)
1、让学生去寻找一些生活中只考虑绝对值的实际例子。
2、课本作业。
课后作业布置
谢
谢
小学用直线上的点表示自然数
情景:某市公交公司在一条东西方向的马路旁设置的站点如图所示,相邻两站之间的距离均为2千米。
西
东
公园
书店
学校
科技馆
小区
问题1:
如果你在学校站点处,怎样说明其他站点的位置呢?
小提示:要注意参照点的选择、距离和方向
西
东
公园
书店
学校
科技馆
小区
问题2:
以学校为参照点,并用0表示该点,规定学校以东的位置用正数表示,学校以西的位置用负数表示,以1千米为单位长度,请你在图中用有理数标出所有站点的位置。
0
2
4
-2
-4
西
东
公园
书店
学校
科技馆
小区
问题3:
在学校东3千米处是华龙超市,学校西1千米处是东方商场,请你在途中标出他们的位置及其对应的有理数。
0
2
4
-2
-4
3
1
-1
-3
西
东
2
4
-2
-4
3
1
-1
-3
0
0
概念:
规定了原点、正方向和单位长度的直线叫做数轴。
数轴的特征:
1.数轴是一条直线,可以向两端无限延伸;
2.数轴有三要素:原点、单位长度和正方向,三者缺一不可。
做一做
例1、在下图中数轴上的点A,B,C,D分别表示什么数?
例2、画一条数轴,在数轴上标出表示下列各数的点1,-3,-3.5,2.5,4,0。
-1
O
1
-2
-3
2
3
4
-4
A
B
C
D
-1
O
1
-2
-3
2
3
4
-4
-3.5
-3
0
1
2.5
4
解:
练一练
1、课后练习。
2、用数轴把下列各数表示出来。
-500,-200,100,200,300。
归纳:
1、每个有理数都对应数轴上的一个点;
2、有理数0就是原点;
3、表示正有理数的点在原点的右侧,表示负有理数的点在原点的左侧;
4、单位长度可根据实际需要来确定。
测一测
1、数轴的三要素是
、
、
。
2、数轴上与原点之间的距离小于5的表示整数的点共有
个,它们表示的数是
。
想一想
超市、书店、玩具店依次坐落在一条东西走向的大街上,超市在书店西边20米处,玩具店位于书店东边50米处。小明从书店出来沿街向东走了50米,接着又向西走了80米,此时小明的位置在何处?在数轴上标出超市、书店、玩具店的位置,以及小明最后的位置。
总结反思
本节课你有什么收获、谈谈你的体会。
点评:数轴在数学中有着重要的地位,它是数形结合的起点,是我们理解数学,学好数学的重要思想方法,同时数轴是非常重要的工具,它使数和直线上的点建立了对应关系,为我们今后进一步研究问题提供了新方法和新思想。
谢
谢
法布尔:(1823—1915)法国著名科学家、科普作家。从小生活贫困,15岁考入师范学校,毕业后在初中教数学。一次带学生上户外几何课,忽然在石块上发现垒筑蜂和蜂窝,从此“虫心”焕发。他花了一个月的工资,买了一本昆虫学著作,立志做一个为虫子写历史的人。他穷毕生之力深入昆虫世界,在自然环境中对昆虫进行观察和实验,真实地记录下昆虫的本能与习性,写成10册之巨的《昆虫记》。
动物是凭借什么来辨别方向、认识路线的呢?科学家们利用蜜蜂和鸽子所做的动物导航实验,已经初步揭开了这两种动物导航的秘密。著名的诺贝尔奖金获得者、奥地利生物学家弗里希,曾在20世纪40年代,用一系列实验测出了蜜峰的基本导航能力,证明了蜜蜂通常是利用太阳作为罗盘进行导航的,指出蜜蜂就是以太阳作为参照点,通过“舞蹈”告诉其他蜜蜂如何到达它发现的花源地。
1.这篇课文讲了一件什么事?
2.为了验证蜜蜂有没有辨别方向的能力,作者是怎么做的,结论又是怎样的?
3.作者的结论是怎样得出的?
无论
纸袋
证实
飞散
几乎
大概
减少
阻力
遥远
推测
包括
检查
迷失
准确无误
沿途
确确实实
超常 记忆力
课堂初读课文
①自读课文。画出不认识的字,读准字音,读通句子。
②同桌互读,纠正错误。
学习第一自然段。
a.读一读。谁愿意把第一自然段读给大家听听?
b.想一想。知道“我”想做个什么试验吗?
c.说一说。假如是你,你想怎样做这个试验?
学习第二至七自然段。
a.读一读。下面我们来仔细研究一下作者是怎样试验的,请读第二自然段。
b.画一画。画出能表示作者试验做法的词语或句子。
c.写一写。请若干学生把画出的语句写到黑板上。
d.议一议。
学习第八自然段。
a.读一读。实验的结果是怎样的?
b.谈一谈。实验说明了什么结论?
C.议一议。实验给我们了什么启示?
谢
谢
数轴
绝对值与相反数
什么是数轴?
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
数轴是规定了原点、正方向、单位长度的直线。
上面过程说明了什么?
0
-4
-3
-2
-1
3
2
1
-3
+3
原点
在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点的距离相等。
回顾思考
看谁答得快?
1.在数轴上,离开原点的距离有4个单位的数是(
)
2.汽车从A地出发向东行驶20千米,再向西行驶30千米,此时汽车停在何处?
+4和-4
汽车共行驶多少千米?
A
创设问题情境
1、两只小狗从同一点0出发,在一条笔直的街上跑,一只向右跑3米到达A点,另一只向左跑3米到达B点。若规定向右为正,则A处记做_______,B处记做_______。
2、这两只小狗在跑的过程中,有没有共同的地方?在数轴上的A、B两点又有什么特征?
A
B
小
结:
在实际生活中,有时存在这样的情况,无需考虑数的正负性质,比如:在计算小狗所跑的路程中,与小狗跑的方向无关,这时所走的路程只需用正数,这样就引进了一个新的概念———绝对值。
绝对值:一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
∵
-5到原点的距离是5,
∴
-5的绝对值是5,记|-5|=5;
又:5的绝对值是5,记做|5|=5。
注意:①与原点的关系
②是一个距离的概念
规定
绝对值的几何定义:
例1:求下列各数的绝对值:
解:
应用深化知识
请你举出一些相反数的例子
像3和-3,5和-5等这样符号不同,绝对值相等的数,我们称其中一个是另外一个数的相反数,也称这两个数互为相反数。0的相反数规定为0。
特点:
1、一个正数的绝对值是它本身;
2、一个负数的绝对值是它的相反数;
3、零的绝对值是零;
4、互为相反数的两个数的绝对值相等。
|
5
-
1
|
=
(
)
1
+
|
-5
|
=(
)
|
5
|
-
|
-3
|
=(
)
|
-1
|
×
|
-2
|
=(
)
|
-6.2
|
÷
|
+2
|
=(
)
填一填
分析:先求算式中绝对值的值,然后进行四则运算。
(1)一个数的绝对值一定是正数。
(
)
(2)一个数的绝对值不可能是负数。
(
)
(3)互为相反数的两个数,它们的绝对值一定相等。(
)
(4)绝对值是同一个正数的数有两个,且它们是互为相反数。
(
)
探索挑战
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
问题1:字母a表示一个数,-a表示什么?-a一定是负数吗?
问题2:如果数a的绝对值等于a,那么a可能是正数吗?可能是负数吗?可能是零吗?
问题3:如果数a的绝对值等于-a,那么a可能是正数吗?可能是负数吗?可能是零吗?
归纳:
1.绝对值的定义;
2.绝对值的性质:
(1)正数的绝对值是它本身;
(2)负数的绝对值是它的相反数;
(3)0的绝对值是0;
(4)互为相反数的两个数的绝对值相等。
归纳小结反思
练习:回答下列问题
①一个数的绝对值是它本身,这个数是什么数?
②一个数的绝对值是它的相反数,这个数是什么数?
③一个数的绝对值一定是正数吗?
④一个数的绝对值不可能是负数,对吗?
(正数和零)
(负数和零)
(不一定)
(对)
1、让学生去寻找一些生活中只考虑绝对值的实际例子。
2、课本作业。
课后作业布置
谢
谢
小学用直线上的点表示自然数
情景:某市公交公司在一条东西方向的马路旁设置的站点如图所示,相邻两站之间的距离均为2千米。
西
东
公园
书店
学校
科技馆
小区
问题1:
如果你在学校站点处,怎样说明其他站点的位置呢?
小提示:要注意参照点的选择、距离和方向
西
东
公园
书店
学校
科技馆
小区
问题2:
以学校为参照点,并用0表示该点,规定学校以东的位置用正数表示,学校以西的位置用负数表示,以1千米为单位长度,请你在图中用有理数标出所有站点的位置。
0
2
4
-2
-4
西
东
公园
书店
学校
科技馆
小区
问题3:
在学校东3千米处是华龙超市,学校西1千米处是东方商场,请你在途中标出他们的位置及其对应的有理数。
0
2
4
-2
-4
3
1
-1
-3
西
东
2
4
-2
-4
3
1
-1
-3
0
0
概念:
规定了原点、正方向和单位长度的直线叫做数轴。
数轴的特征:
1.数轴是一条直线,可以向两端无限延伸;
2.数轴有三要素:原点、单位长度和正方向,三者缺一不可。
做一做
例1、在下图中数轴上的点A,B,C,D分别表示什么数?
例2、画一条数轴,在数轴上标出表示下列各数的点1,-3,-3.5,2.5,4,0。
-1
O
1
-2
-3
2
3
4
-4
A
B
C
D
-1
O
1
-2
-3
2
3
4
-4
-3.5
-3
0
1
2.5
4
解:
练一练
1、课后练习。
2、用数轴把下列各数表示出来。
-500,-200,100,200,300。
归纳:
1、每个有理数都对应数轴上的一个点;
2、有理数0就是原点;
3、表示正有理数的点在原点的右侧,表示负有理数的点在原点的左侧;
4、单位长度可根据实际需要来确定。
测一测
1、数轴的三要素是
、
、
。
2、数轴上与原点之间的距离小于5的表示整数的点共有
个,它们表示的数是
。
想一想
超市、书店、玩具店依次坐落在一条东西走向的大街上,超市在书店西边20米处,玩具店位于书店东边50米处。小明从书店出来沿街向东走了50米,接着又向西走了80米,此时小明的位置在何处?在数轴上标出超市、书店、玩具店的位置,以及小明最后的位置。
总结反思
本节课你有什么收获、谈谈你的体会。
点评:数轴在数学中有着重要的地位,它是数形结合的起点,是我们理解数学,学好数学的重要思想方法,同时数轴是非常重要的工具,它使数和直线上的点建立了对应关系,为我们今后进一步研究问题提供了新方法和新思想。
谢
谢
法布尔:(1823—1915)法国著名科学家、科普作家。从小生活贫困,15岁考入师范学校,毕业后在初中教数学。一次带学生上户外几何课,忽然在石块上发现垒筑蜂和蜂窝,从此“虫心”焕发。他花了一个月的工资,买了一本昆虫学著作,立志做一个为虫子写历史的人。他穷毕生之力深入昆虫世界,在自然环境中对昆虫进行观察和实验,真实地记录下昆虫的本能与习性,写成10册之巨的《昆虫记》。
动物是凭借什么来辨别方向、认识路线的呢?科学家们利用蜜蜂和鸽子所做的动物导航实验,已经初步揭开了这两种动物导航的秘密。著名的诺贝尔奖金获得者、奥地利生物学家弗里希,曾在20世纪40年代,用一系列实验测出了蜜峰的基本导航能力,证明了蜜蜂通常是利用太阳作为罗盘进行导航的,指出蜜蜂就是以太阳作为参照点,通过“舞蹈”告诉其他蜜蜂如何到达它发现的花源地。
1.这篇课文讲了一件什么事?
2.为了验证蜜蜂有没有辨别方向的能力,作者是怎么做的,结论又是怎样的?
3.作者的结论是怎样得出的?
无论
纸袋
证实
飞散
几乎
大概
减少
阻力
遥远
推测
包括
检查
迷失
准确无误
沿途
确确实实
超常 记忆力
课堂初读课文
①自读课文。画出不认识的字,读准字音,读通句子。
②同桌互读,纠正错误。
学习第一自然段。
a.读一读。谁愿意把第一自然段读给大家听听?
b.想一想。知道“我”想做个什么试验吗?
c.说一说。假如是你,你想怎样做这个试验?
学习第二至七自然段。
a.读一读。下面我们来仔细研究一下作者是怎样试验的,请读第二自然段。
b.画一画。画出能表示作者试验做法的词语或句子。
c.写一写。请若干学生把画出的语句写到黑板上。
d.议一议。
学习第八自然段。
a.读一读。实验的结果是怎样的?
b.谈一谈。实验说明了什么结论?
C.议一议。实验给我们了什么启示?
谢
谢
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
