人教版八年级上册14.1.2 幂的乘方课件(16张)
文档属性
| 名称 | 人教版八年级上册14.1.2 幂的乘方课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 268.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 14:04:03 | ||
图片预览






文档简介
(共16张PPT)
14.1.2
幂的乘方
(1)理解幂的乘方,会用这一性质进行幂的乘方运算.
?(2)体验“由特殊到一般,从具体到抽象”的思想方法,在研究数学问题中的作用.
学习目标
回顾与思考
回顾
&
思考
?
?
?
乘方的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an
=
?
am+n
(m,n都是正整数)
1计算下列各式,并说明所依据的运算性质:
(1)102×104=____
(2)an+1·an-1=_____
(3)2n·2n=____
(4)x2·x2·x2·x2=____
106
a2n
22n
x8
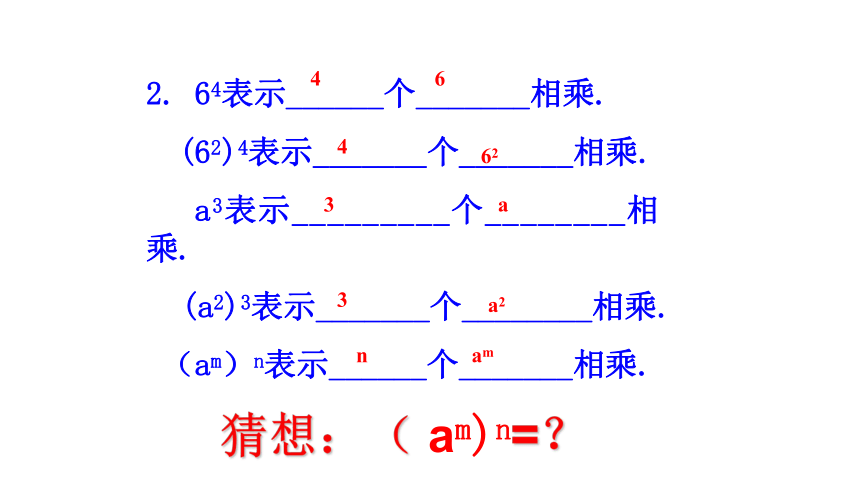
2.
64表示______个_______相乘.
(62)4表示_______个_______相乘.
a3表示_________个________相乘.
(a2)3表示_______个________相乘.
(am)n表示______个_______相乘.
4
6
4
62
3
a
3
a2
n
am
猜想:(
am)n=?
(1)(103)3=
×
×
=10
+
+
=10
×
.
(2)(a2)3=
×
×
=
a
+
+
=a
×
.
(3)(am)3=
×
×
=
a
+
+
=a
×
.
活动1:根据乘方的意义及同底数幂的乘法填空.
103
103
103
3
3
a2
a2
a2
2
2
2
3
3
3
2
3
am
am
am
m
m
m
m
3
乘方的意义
同底数幂
乘法性质
乘法意义
(4)(am)n=
×
×
=
a
+
+
=a
×
.
am
am
…
m
…
m
m
n
n个am相乘
n个m相加
幂的乘方性质:
幂的乘方,底数不变,指数相乘.
(m、n是正整数)
(am)n=
amn
符号语言:
文字语言:
合作探究
的证明
在下面的推导中,说明每一步(变形)的依据:
(am)n
=
am·am·……·am
(
)
=am+m+m….+m
(
)
=amn
乘方的意义
同底数幂乘法
的性质
n个am
n个m
?
?
(am)n
=
amn
练习1、判断对错,如果有错,如何改正?
(1)(mn)2=m2n
(2)(m2)3=m5
(3)-(m3)2=-m6
(4)m2·m3=m6
(5)m3+m3=m6
运用对比
√
×
(m2)3=m2?3=m6
√
×
m2·m3=m2+3=m5
×
m3+m3=2m3
(1)
(103)4
(2)
(c2)3
(3)
(a4)m
(4)?
x
·
(x2)5
(5)
(a4)3+m
例1:计算
同桌仿例1做编题游戏
解:
(103)4
=103
×4=1012
(2)
(c2)3
=
c2
×3=c6
(3)
(a4)m
=a4
×
m=a4m
(4)?
x
·
(x2)5
=x
·
x2
×
5=x1+10=x11
(5)
(a4)3+m
=a4
×(3+m)
=a12+4m
1.计算:
(1)(x3)4·x2
.(2)
2(x2)n-(xn)2
.(3)[(x2)3]7
.
(1)原式=
x12
·x2
=
x14.
(2)原式=
2x2n
-x2n
=x2n.
(3)原式=(x2)21
=
x42.
解:
【跟踪训练】
思考
(-x4)3和(-x3)4的计算结果一样吗?为什么?
不一样,(-x4)3=-x12,(-x3)4=x12.
幂的乘方与同底数幂的乘法的区别
运算法则是底数不变,指数相加.
同底数幂的乘法
几个相同的数的乘积
运算法则是底数不变,指数相乘.
幂的乘方
几个相同的幂的乘积
幂的乘方与同底数幂的乘法的联系
幂的乘方可以转化为同底数幂相乘,如(a3)2
=a3·a3;当指数相同的两个同底数幂相乘时,可以转化为幂的乘方,如a3·a3=(a3)2.
课堂练习
1、选择题:下列各式计算正确的是(
)
A.
3a2-a2=2
B.
(a2)3·a4=a24
C.
(a2)3·a+a7=2a7
D.
-
(a2)4=a8
2、计算题:
(1)
(75)2
(2)
(-4n)5
(3)
(a3)m
(4)
(a3)4·a2
3、若a2n=3,求(a3n)4的值.
(选做)
4.
(1)若2x+y=3,则4x·2y=
.
(2)已知3m·9m·27m·81m=330,求m的值.
8
解:3m·32m·33m·34m=330
310m=330
m=3
拓展与提高:
1.如果am=2,
an=3,那么a3m-a2n和a3m+2n的值分别是
______。
3.比较340与430的大小。
2.已知9x=310,则x的值是______。
-1,
72
5
因为:340=(34)10
=8110
;
430=(43)10=6410
又因为
81
﹥
64,所以8110﹥6410.
所以:
340
﹥
430
.
14.1.2
幂的乘方
(1)理解幂的乘方,会用这一性质进行幂的乘方运算.
?(2)体验“由特殊到一般,从具体到抽象”的思想方法,在研究数学问题中的作用.
学习目标
回顾与思考
回顾
&
思考
?
?
?
乘方的意义:
a·a·
…
·a
n个a
an
=
同底数幂的乘法运算法则:
am
·
an
=
?
am+n
(m,n都是正整数)
1计算下列各式,并说明所依据的运算性质:
(1)102×104=____
(2)an+1·an-1=_____
(3)2n·2n=____
(4)x2·x2·x2·x2=____
106
a2n
22n
x8
2.
64表示______个_______相乘.
(62)4表示_______个_______相乘.
a3表示_________个________相乘.
(a2)3表示_______个________相乘.
(am)n表示______个_______相乘.
4
6
4
62
3
a
3
a2
n
am
猜想:(
am)n=?
(1)(103)3=
×
×
=10
+
+
=10
×
.
(2)(a2)3=
×
×
=
a
+
+
=a
×
.
(3)(am)3=
×
×
=
a
+
+
=a
×
.
活动1:根据乘方的意义及同底数幂的乘法填空.
103
103
103
3
3
a2
a2
a2
2
2
2
3
3
3
2
3
am
am
am
m
m
m
m
3
乘方的意义
同底数幂
乘法性质
乘法意义
(4)(am)n=
×
×
=
a
+
+
=a
×
.
am
am
…
m
…
m
m
n
n个am相乘
n个m相加
幂的乘方性质:
幂的乘方,底数不变,指数相乘.
(m、n是正整数)
(am)n=
amn
符号语言:
文字语言:
合作探究
的证明
在下面的推导中,说明每一步(变形)的依据:
(am)n
=
am·am·……·am
(
)
=am+m+m….+m
(
)
=amn
乘方的意义
同底数幂乘法
的性质
n个am
n个m
?
?
(am)n
=
amn
练习1、判断对错,如果有错,如何改正?
(1)(mn)2=m2n
(2)(m2)3=m5
(3)-(m3)2=-m6
(4)m2·m3=m6
(5)m3+m3=m6
运用对比
√
×
(m2)3=m2?3=m6
√
×
m2·m3=m2+3=m5
×
m3+m3=2m3
(1)
(103)4
(2)
(c2)3
(3)
(a4)m
(4)?
x
·
(x2)5
(5)
(a4)3+m
例1:计算
同桌仿例1做编题游戏
解:
(103)4
=103
×4=1012
(2)
(c2)3
=
c2
×3=c6
(3)
(a4)m
=a4
×
m=a4m
(4)?
x
·
(x2)5
=x
·
x2
×
5=x1+10=x11
(5)
(a4)3+m
=a4
×(3+m)
=a12+4m
1.计算:
(1)(x3)4·x2
.(2)
2(x2)n-(xn)2
.(3)[(x2)3]7
.
(1)原式=
x12
·x2
=
x14.
(2)原式=
2x2n
-x2n
=x2n.
(3)原式=(x2)21
=
x42.
解:
【跟踪训练】
思考
(-x4)3和(-x3)4的计算结果一样吗?为什么?
不一样,(-x4)3=-x12,(-x3)4=x12.
幂的乘方与同底数幂的乘法的区别
运算法则是底数不变,指数相加.
同底数幂的乘法
几个相同的数的乘积
运算法则是底数不变,指数相乘.
幂的乘方
几个相同的幂的乘积
幂的乘方与同底数幂的乘法的联系
幂的乘方可以转化为同底数幂相乘,如(a3)2
=a3·a3;当指数相同的两个同底数幂相乘时,可以转化为幂的乘方,如a3·a3=(a3)2.
课堂练习
1、选择题:下列各式计算正确的是(
)
A.
3a2-a2=2
B.
(a2)3·a4=a24
C.
(a2)3·a+a7=2a7
D.
-
(a2)4=a8
2、计算题:
(1)
(75)2
(2)
(-4n)5
(3)
(a3)m
(4)
(a3)4·a2
3、若a2n=3,求(a3n)4的值.
(选做)
4.
(1)若2x+y=3,则4x·2y=
.
(2)已知3m·9m·27m·81m=330,求m的值.
8
解:3m·32m·33m·34m=330
310m=330
m=3
拓展与提高:
1.如果am=2,
an=3,那么a3m-a2n和a3m+2n的值分别是
______。
3.比较340与430的大小。
2.已知9x=310,则x的值是______。
-1,
72
5
因为:340=(34)10
=8110
;
430=(43)10=6410
又因为
81
﹥
64,所以8110﹥6410.
所以:
340
﹥
430
.
