人教版九年级上册数学 24.2.2直线和圆的位置关系练习 (word版 无答案)
文档属性
| 名称 | 人教版九年级上册数学 24.2.2直线和圆的位置关系练习 (word版 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 28.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览

文档简介
24.2.2 直线和圆的位置关系
一、切线的性质定理的运用:
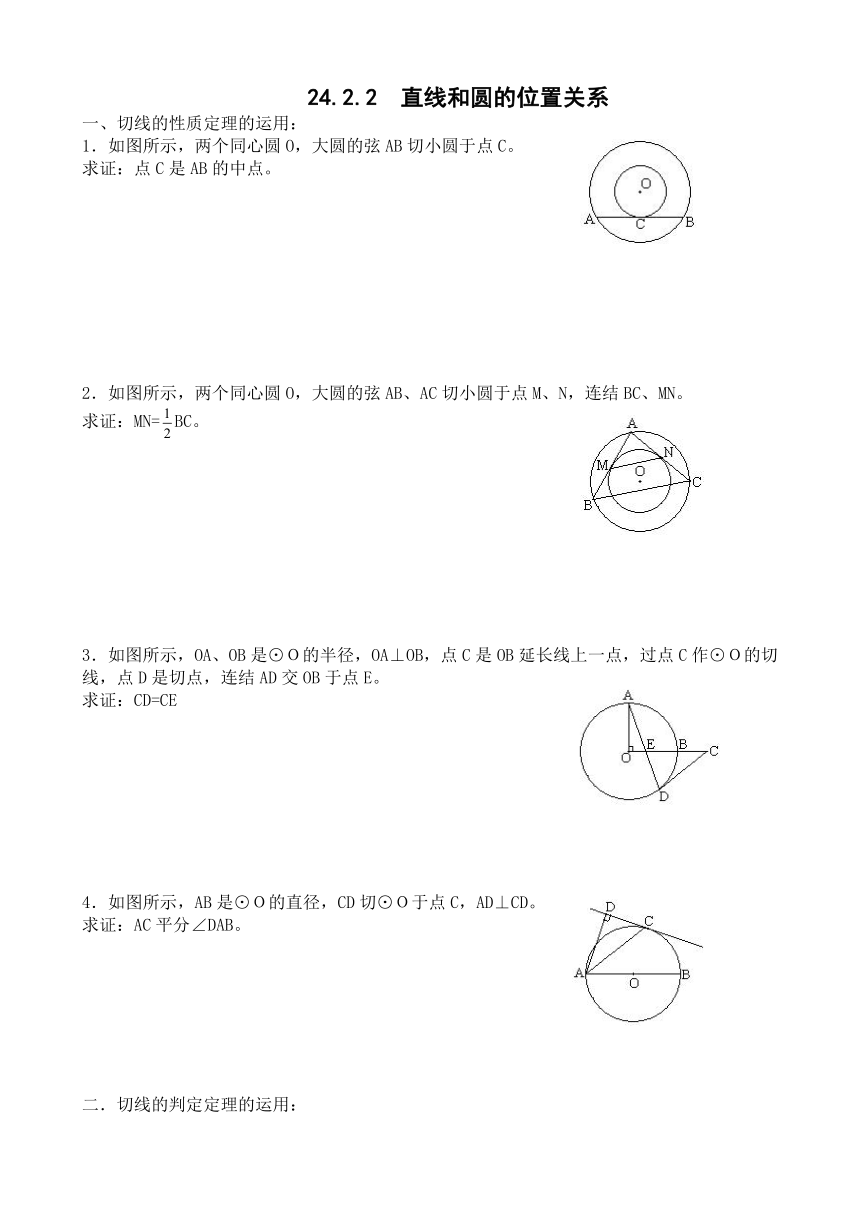
1.如图所示,两个同心圆O,大圆的弦AB切小圆于点C。
求证:点C是AB的中点。
2.如图所示,两个同心圆O,大圆的弦AB、AC切小圆于点M、N,连结BC、MN。
求证:MN=BC。
3.如图所示,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连结AD交OB于点E。
求证:CD=CE
4.如图所示,AB是⊙O的直径,CD切⊙O于点C,AD⊥CD。
求证:AC平分∠DAB。
二.切线的判定定理的运用:
1.如图所示,AB是⊙O的直径,点C在⊙O上,AC平分∠DAB
,AD⊥CD。
求证:CD与⊙O相切。
2.如图所示,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,,点D在⊙O上,连结AD交OB于点E,且CD=CE。
求证:CD与⊙O相切。
3.如图所示,点O是∠BAC的平分线AD上一点,以O为圆心的与AB相切于点M。
求证:AC与⊙O相切。
4.如图所示,AB是⊙O的直径,点D在⊙O上,BC是⊙O的切线,AD∥OC。
求证:CD是⊙O的切线。
5.如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC。
求证:⑴点D是BC的中点;
⑵DE是⊙O的切线。
三、拓展提高
1.已知圆的直径为1.3cm,圆心到直线z的距离为6cm,那么直线l和这个圆的公共点的个数是
.
2.已知⊙0半径为4cm,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是
3.圆心O到直线l的距离为d,⊙O的半径为r,当d与r是方程x2-9x+20=0的两根时,直线l与⊙0的位置关系是
.
4.填空
(1)已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是
___
_。
(2)已知3
⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
5.已知⊙O的直径为12cm.
(1)若圆心O到直线l的距离为12cm,则直线l与⊙O
的位置关系为________;
(2)若圆心O到直线l的距离为6cm,则直线l与⊙O
的位置关系为________;
(3)若圆心O到直线l的距离为3cm,则直线l与⊙O
的位置关系为________.
6.设⊙0的半径为r,圆心O到直线l的距离为d,若直线l与⊙0有交点,则d与r的关系是(
).
A.d=r
B.dC.d>r
D.d≤r
7.直线和圆相交,圆的半径为r,且直线到圆心的距离为5,则有(
)
A.
r
<
5
B.
r
>
5
C.
r
=
5
D.
r
≥
5
8.⊙O的最大弦长为8,直线与⊙O相离,若圆心O到直线的距离为d,则有(
)
A.
d
>
8
B.
d
<
8
C.
d
>
4
D.
d
<
4
9.若直线与⊙O至少有一个公共点,
则此直线与⊙O的位置关系是
(
)
A.
相交或相切
B.
相交或相离
C.
相切或相离
D.
上三种情况都有可能
一、切线的性质定理的运用:
1.如图所示,两个同心圆O,大圆的弦AB切小圆于点C。
求证:点C是AB的中点。
2.如图所示,两个同心圆O,大圆的弦AB、AC切小圆于点M、N,连结BC、MN。
求证:MN=BC。
3.如图所示,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,过点C作⊙O的切线,点D是切点,连结AD交OB于点E。
求证:CD=CE
4.如图所示,AB是⊙O的直径,CD切⊙O于点C,AD⊥CD。
求证:AC平分∠DAB。
二.切线的判定定理的运用:
1.如图所示,AB是⊙O的直径,点C在⊙O上,AC平分∠DAB
,AD⊥CD。
求证:CD与⊙O相切。
2.如图所示,OA、OB是⊙O的半径,OA⊥OB,点C是OB延长线上一点,,点D在⊙O上,连结AD交OB于点E,且CD=CE。
求证:CD与⊙O相切。
3.如图所示,点O是∠BAC的平分线AD上一点,以O为圆心的与AB相切于点M。
求证:AC与⊙O相切。
4.如图所示,AB是⊙O的直径,点D在⊙O上,BC是⊙O的切线,AD∥OC。
求证:CD是⊙O的切线。
5.如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC。
求证:⑴点D是BC的中点;
⑵DE是⊙O的切线。
三、拓展提高
1.已知圆的直径为1.3cm,圆心到直线z的距离为6cm,那么直线l和这个圆的公共点的个数是
.
2.已知⊙0半径为4cm,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是
3.圆心O到直线l的距离为d,⊙O的半径为r,当d与r是方程x2-9x+20=0的两根时,直线l与⊙0的位置关系是
.
4.填空
(1)已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是
___
_。
(2)已知3
⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
5.已知⊙O的直径为12cm.
(1)若圆心O到直线l的距离为12cm,则直线l与⊙O
的位置关系为________;
(2)若圆心O到直线l的距离为6cm,则直线l与⊙O
的位置关系为________;
(3)若圆心O到直线l的距离为3cm,则直线l与⊙O
的位置关系为________.
6.设⊙0的半径为r,圆心O到直线l的距离为d,若直线l与⊙0有交点,则d与r的关系是(
).
A.d=r
B.d
D.d≤r
7.直线和圆相交,圆的半径为r,且直线到圆心的距离为5,则有(
)
A.
r
<
5
B.
r
>
5
C.
r
=
5
D.
r
≥
5
8.⊙O的最大弦长为8,直线与⊙O相离,若圆心O到直线的距离为d,则有(
)
A.
d
>
8
B.
d
<
8
C.
d
>
4
D.
d
<
4
9.若直线与⊙O至少有一个公共点,
则此直线与⊙O的位置关系是
(
)
A.
相交或相切
B.
相交或相离
C.
相切或相离
D.
上三种情况都有可能
同课章节目录
