人教版数学九年级上册:24.2.2 切线的判定定理 课件(14张)
文档属性
| 名称 | 人教版数学九年级上册:24.2.2 切线的判定定理 课件(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 142.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 14:13:25 | ||
图片预览



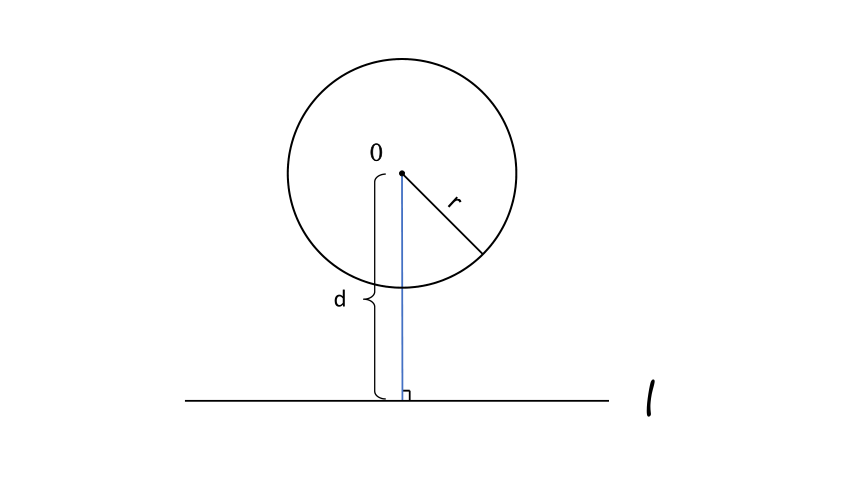

文档简介
(共14张PPT)
24.2.2
切线的判定定理
人教版九年级上册
直线与圆的
位置关系
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系(数量)
2个
交点
割线
1个
切点
切线
d
<
r
d
=
r
d
>
r
没有
回顾:
相交
相切
相离
判断直线和圆的位置关系,有几种方法?
一、公共点的个数
二、圆心到直线的距离与半径作比较(d
r法常用)
O
l
O
r
d
l
点A叫半径OA的外端
作半径OA
经过点A作直线
与圆O的位置关系
相交
相切
无数条
O
·A
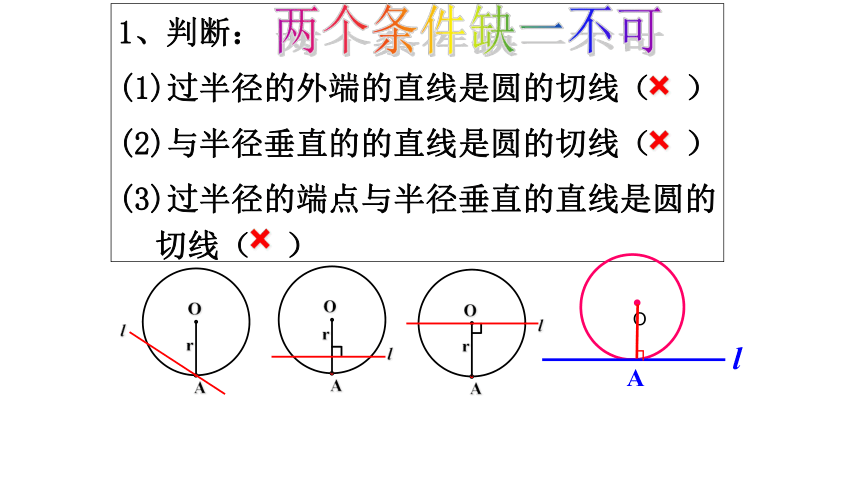
1、判断:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
两个条件缺一不可
●
O
┐
A
l
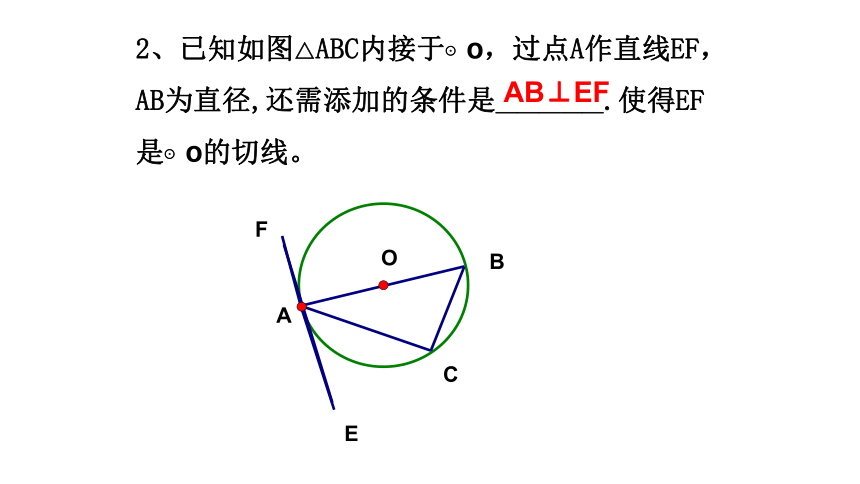
2、已知如图△ABC内接于⊙O,过点A作直线EF,AB为直径,还需添加的条件是_____.使得EF是⊙O的切线。
F
E
C
O
B
A
AB⊥EF
例1、如图
AB是⊙O的直径,∠ABT=45°AT=AB,求证:AT
是⊙O的切线.
证明:
∵
∠1
=
45°,AT=AB
∴
∠T
=
∠1=45
°.
∴
∠TAB
=
180°-∠T-∠1
=
90°.
∴
TA⊥OA.
∴
AT是⊙O的切线.
·
A
B
T
O
∵
OA是⊙O的半径,
定理应用:
1
例2、
如图,已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
有交点,连半径,证垂直
定理应用:
例3、
如图,已知:O为∠BAC平分线上一
点,OD⊥AB于D,以O为圆心,OD为半径作
⊙O。求证:⊙O与AC相切。
O
A
B
C
E
D
无交点,作垂直,证半径
定理应用:
O
B
A
C
O
A
B
C
E
D
归纳:
例2与例3的证法有何不同?
(1)有交点,连半径,证垂直.
(2)无交点,
作垂直,证半径.
练习1、如图,在△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E.
求证:PE是⊙O的切线.
E
O
A
B
C
P
有交点,连半径,证垂直
练习2、如图,△ABC中,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O.
求证:AB是⊙O的切线.
F
E
C
O
B
A
无交点,作垂直,证半径
练习3、如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上,
∠CAB=30°.
求证:DC是⊙O的切线.
A
B
C
D
O
有交点,连半径,证垂直
24.2.2
切线的判定定理
人教版九年级上册
直线与圆的
位置关系
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系(数量)
2个
交点
割线
1个
切点
切线
d
<
r
d
=
r
d
>
r
没有
回顾:
相交
相切
相离
判断直线和圆的位置关系,有几种方法?
一、公共点的个数
二、圆心到直线的距离与半径作比较(d
r法常用)
O
l
O
r
d
l
点A叫半径OA的外端
作半径OA
经过点A作直线
与圆O的位置关系
相交
相切
无数条
O
·A
1、判断:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
两个条件缺一不可
●
O
┐
A
l
2、已知如图△ABC内接于⊙O,过点A作直线EF,AB为直径,还需添加的条件是_____.使得EF是⊙O的切线。
F
E
C
O
B
A
AB⊥EF
例1、如图
AB是⊙O的直径,∠ABT=45°AT=AB,求证:AT
是⊙O的切线.
证明:
∵
∠1
=
45°,AT=AB
∴
∠T
=
∠1=45
°.
∴
∠TAB
=
180°-∠T-∠1
=
90°.
∴
TA⊥OA.
∴
AT是⊙O的切线.
·
A
B
T
O
∵
OA是⊙O的半径,
定理应用:
1
例2、
如图,已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
有交点,连半径,证垂直
定理应用:
例3、
如图,已知:O为∠BAC平分线上一
点,OD⊥AB于D,以O为圆心,OD为半径作
⊙O。求证:⊙O与AC相切。
O
A
B
C
E
D
无交点,作垂直,证半径
定理应用:
O
B
A
C
O
A
B
C
E
D
归纳:
例2与例3的证法有何不同?
(1)有交点,连半径,证垂直.
(2)无交点,
作垂直,证半径.
练习1、如图,在△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E.
求证:PE是⊙O的切线.
E
O
A
B
C
P
有交点,连半径,证垂直
练习2、如图,△ABC中,AB=AC,AO⊥BC于O,OE⊥AC于E,以O为圆心,OE为半径作⊙O.
求证:AB是⊙O的切线.
F
E
C
O
B
A
无交点,作垂直,证半径
练习3、如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上,
∠CAB=30°.
求证:DC是⊙O的切线.
A
B
C
D
O
有交点,连半径,证垂直
同课章节目录
