人教版数学九年级上册:24.2.2 直线和圆的位置关系-课件(14张)
文档属性
| 名称 | 人教版数学九年级上册:24.2.2 直线和圆的位置关系-课件(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 970.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 14:15:26 | ||
图片预览


文档简介
(共14张PPT)
请在此处添加标题
请在此处添加副标题
24.2.2直线与圆的位置关系
点和圆的位置关系有哪几种?
(1)d(2)d=r
(3)d>r
A
B
C
d
点A在圆内
点B在圆上
点C
在圆外
三种位置关系
O
点到圆心距离为d
⊙O半径为r
回顾:
●O
●O
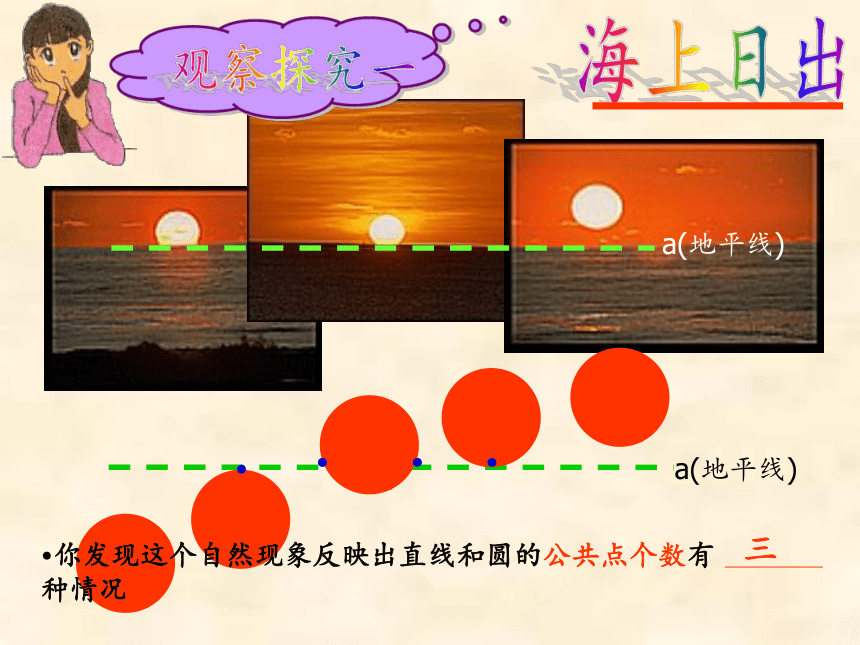
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
a(地平线)
a(地平线)
●O
●O
●O
三
你发现这个自然现象反映出直线和圆的公共点个数有
种情况
海上日出
观察探究一
●
●
●
●
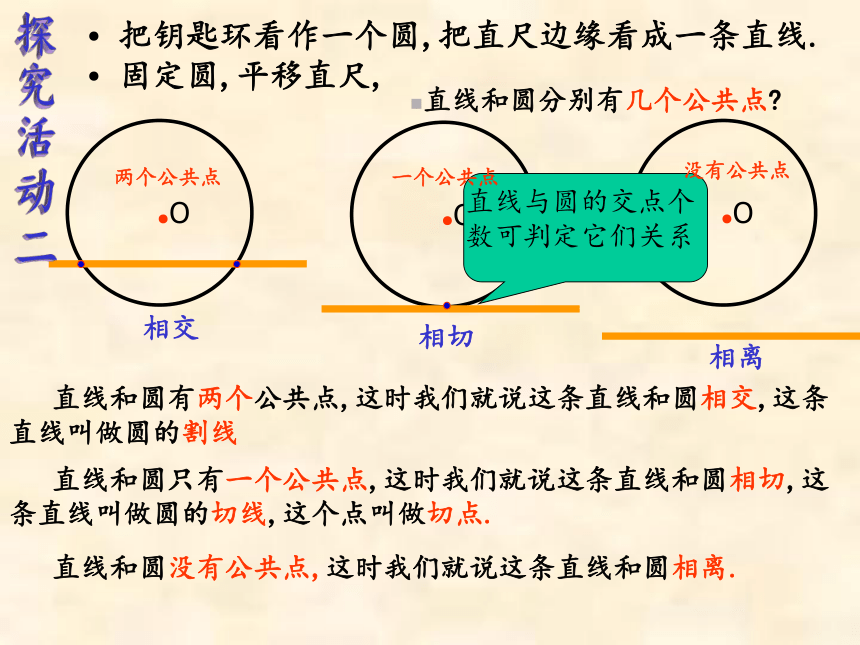
把钥匙环看作一个圆,把直尺边缘看成一条直线.
固定圆,平移直尺,
直线和圆分别有几个公共点?
●O
●O
相交
●O
相切
相离
直线与圆的交点个数可判定它们关系
探究活动二
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线
直线和圆没有公共点,这时我们就说这条直线和圆相离.
两个公共点
没有公共点
一个公共点
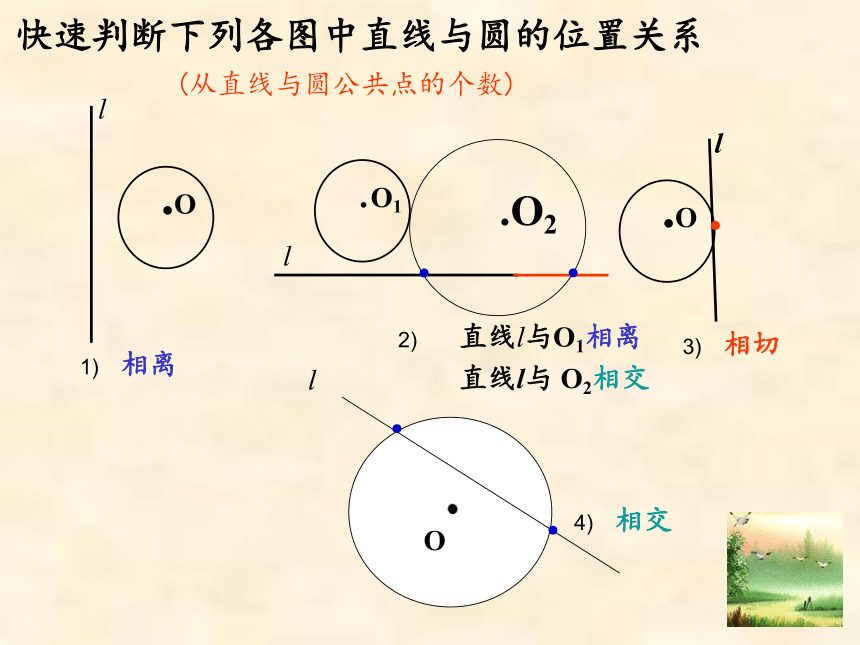
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1相离
直线l与
O2相交
O
(从直线与圆公共点的个数)
●
●
●
●
●
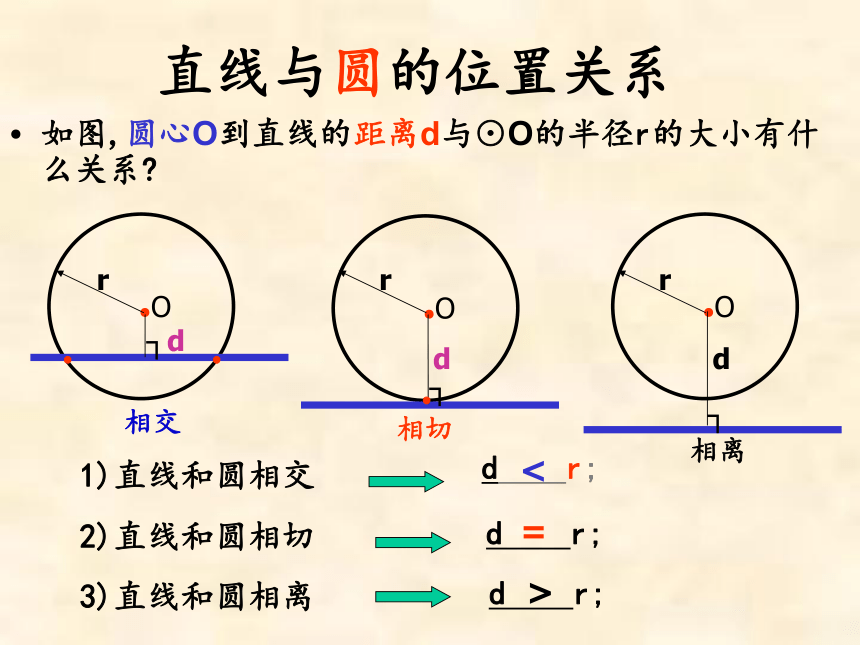
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系?
●O
●O
相交
●O
相切
相离
直线与圆的位置关系
r
r
r
┐d
d
┐
d
┐
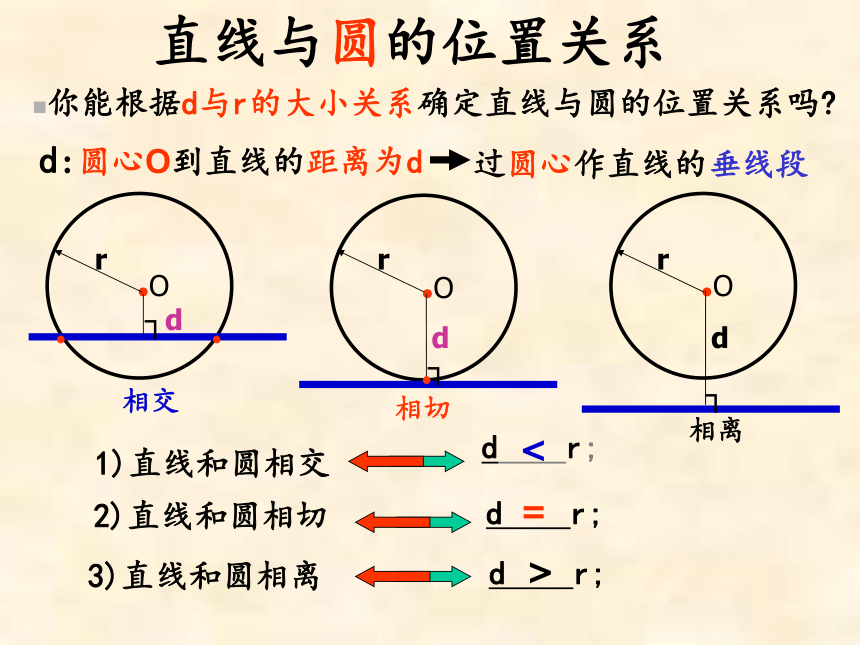
1)直线和圆相交
d
r;
d
r;
2)直线和圆相切
3)直线和圆相离
d
r;
<
=
>
1)直线和圆相交
d
r;
d
r;
2)直线和圆相切
3)直线和圆相离
d
r;
直线与圆的位置关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
你能根据d与r的大小关系确定直线与圆的位置关系吗?
过圆心作直线的垂线段
d:圆心O到直线的距离为d
练习2 已知⊙A
的直径为
6,点
A
的坐标为(-3,
-4),则⊙A
与
x
轴的位置关系是_____,⊙A
与
y
轴的位置关系是______.
相离
相切
轻松闯关
y
x
A
-3
-4
O
判定直线
与圆的位置关系的方法有____种:
(1)根据定义,由______
__________
的个数来判断;
(2)由________________
_
的大小关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳:
如图:∠AOB
=
30°,M是OB上的一点,且OM
=5
cm
以M为圆心,以r
为半径的圆与直线OA
有怎样的关系?为什么?
(1)r
=
2
cm
;
(2)
r
=
4
cm
;
(3)
r
=
2.5
cm
.
C
O
B
A
M
5
30°
解:
过
M
作
MC⊥OA
于
C,在
Rt
△OMC
中,
∠AOB
=
30°
MC=
OM=
x5=2.5
1
2
1
2
即圆心
M
到OA的距离
d
=
2.5
cm.
因此⊙M
和直线OA
相离.
(3)
当
r
=
2.5cm
时,
因此⊙M
和直线OA
相切.
(1)
当r
=
2
cm
时,
(2)
当
r
=
4
cm
时,
因此⊙M
和直线OA
相交.
2.5
有
d
>
r,
有
d
<
r,
有
d
=
r
,
典型例题
如图:M是OB上的一点,且OM
=5
cm,
以M为圆心,半径r=2.5cm作⊙M.
试问过O的射线OA与OB所夹的锐角a取什么值时射线OA与⊙M
1)相离
(2)相切
(3)相交
?
C
O
B
A
M
5
a
2.5
例题的变式题
解:
过
M
作
MC⊥OA
于
C
1)当∠a
=
30°时,d=CM=2.5=r
此时射线OA与⊙M相切
2)当
30°<∠a
<
时
射线OA与⊙M相离
3)当∠a
<30°时
射线OA与⊙M相交
90°
设⊙O的圆心O到直线的距离为d,半径为r,d.r是
方程(m+9)x2-
(m+6)
x
+1=0的两根,且直线与⊙O相切
时,求m的值?
中考链接
d=r
析:直线与⊙O相切
b2-4ac=0
[-(m+6)]2-4(m+9)=0
解得
m1=
-8
m2=
0
当m=-8时原方程为x2+
2x+1=0
x1=x2=
-1
当m=0时原方程为9x2-
6x+1=0
b2-4ac=
[-(m+6)]2-4(m+9)=0
解:由题意可得
x1=x2=
1
3
∴
m=0
(不符合题意舍去)
直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
蓦然回首
挑战自我:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=2.4cm
(3)
r=3cm.
B
C
A
4
3
D
请在此处添加标题
请在此处添加副标题
24.2.2直线与圆的位置关系
点和圆的位置关系有哪几种?
(1)d
(3)d>r
A
B
C
d
点A在圆内
点B在圆上
点C
在圆外
三种位置关系
O
点到圆心距离为d
⊙O半径为r
回顾:
●O
●O
把太阳看成一个圆,地平线看成一条直线,注意观察直线与圆的公共点的个数
a(地平线)
a(地平线)
●O
●O
●O
三
你发现这个自然现象反映出直线和圆的公共点个数有
种情况
海上日出
观察探究一
●
●
●
●
把钥匙环看作一个圆,把直尺边缘看成一条直线.
固定圆,平移直尺,
直线和圆分别有几个公共点?
●O
●O
相交
●O
相切
相离
直线与圆的交点个数可判定它们关系
探究活动二
直线和圆只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线
直线和圆没有公共点,这时我们就说这条直线和圆相离.
两个公共点
没有公共点
一个公共点
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
l
.
1)
2)
3)
4)
相交
相切
相离
直线l与O1相离
直线l与
O2相交
O
(从直线与圆公共点的个数)
●
●
●
●
●
如图,圆心O到直线的距离d与⊙O的半径r的大小有什么关系?
●O
●O
相交
●O
相切
相离
直线与圆的位置关系
r
r
r
┐d
d
┐
d
┐
1)直线和圆相交
d
r;
d
r;
2)直线和圆相切
3)直线和圆相离
d
r;
<
=
>
1)直线和圆相交
d
r;
d
r;
2)直线和圆相切
3)直线和圆相离
d
r;
直线与圆的位置关系
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
你能根据d与r的大小关系确定直线与圆的位置关系吗?
过圆心作直线的垂线段
d:圆心O到直线的距离为d
练习2 已知⊙A
的直径为
6,点
A
的坐标为(-3,
-4),则⊙A
与
x
轴的位置关系是_____,⊙A
与
y
轴的位置关系是______.
相离
相切
轻松闯关
y
x
A
-3
-4
O
判定直线
与圆的位置关系的方法有____种:
(1)根据定义,由______
__________
的个数来判断;
(2)由________________
_
的大小关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线与圆的公共点
圆心到直线的距离d与半径r
归纳:
如图:∠AOB
=
30°,M是OB上的一点,且OM
=5
cm
以M为圆心,以r
为半径的圆与直线OA
有怎样的关系?为什么?
(1)r
=
2
cm
;
(2)
r
=
4
cm
;
(3)
r
=
2.5
cm
.
C
O
B
A
M
5
30°
解:
过
M
作
MC⊥OA
于
C,在
Rt
△OMC
中,
∠AOB
=
30°
MC=
OM=
x5=2.5
1
2
1
2
即圆心
M
到OA的距离
d
=
2.5
cm.
因此⊙M
和直线OA
相离.
(3)
当
r
=
2.5cm
时,
因此⊙M
和直线OA
相切.
(1)
当r
=
2
cm
时,
(2)
当
r
=
4
cm
时,
因此⊙M
和直线OA
相交.
2.5
有
d
>
r,
有
d
<
r,
有
d
=
r
,
典型例题
如图:M是OB上的一点,且OM
=5
cm,
以M为圆心,半径r=2.5cm作⊙M.
试问过O的射线OA与OB所夹的锐角a取什么值时射线OA与⊙M
1)相离
(2)相切
(3)相交
?
C
O
B
A
M
5
a
2.5
例题的变式题
解:
过
M
作
MC⊥OA
于
C
1)当∠a
=
30°时,d=CM=2.5=r
此时射线OA与⊙M相切
2)当
30°<∠a
<
时
射线OA与⊙M相离
3)当∠a
<30°时
射线OA与⊙M相交
90°
设⊙O的圆心O到直线的距离为d,半径为r,d.r是
方程(m+9)x2-
(m+6)
x
+1=0的两根,且直线与⊙O相切
时,求m的值?
中考链接
d=r
析:直线与⊙O相切
b2-4ac=0
[-(m+6)]2-4(m+9)=0
解得
m1=
-8
m2=
0
当m=-8时原方程为x2+
2x+1=0
x1=x2=
-1
当m=0时原方程为9x2-
6x+1=0
b2-4ac=
[-(m+6)]2-4(m+9)=0
解:由题意可得
x1=x2=
1
3
∴
m=0
(不符合题意舍去)
直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
蓦然回首
挑战自我:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;
(2)r=2.4cm
(3)
r=3cm.
B
C
A
4
3
D
同课章节目录
