【A典学案】二次函数-确定二次函数的表达式 1课时 课件(21张PPT)
文档属性
| 名称 | 【A典学案】二次函数-确定二次函数的表达式 1课时 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 16:23:29 | ||
图片预览








文档简介
第二章 二次函数
第14课时 确定二次函数的表达式
北师大版 九年级下册
温故知新
1.解二元一次方程组(或三元一次方程组)有哪些基本方法?
2.什么叫待定系数法?
3.二次函数有哪几种基本形式?与你的小伙伴互相交流.
阅读感知
阅读课本 42~45 页,完成下面的填空:
1.确定二次函数的表达式需要_________个或________个条件.
2.确定二次函数的表达式一般用_________法求解,对不同的已知条件,应灵活设出二次函数的表达形式求解.
(1)在二次函数的各项系数中,若有两个是________的,一个是已知的,即知道图象上_______点的坐标,将两个点的坐标代入,求出两个未知数系数即可求出表达式.
阅读感知
(2)若已知二次函数的_________坐标及图象上另外一点,则可设顶点式(即:y=_________),将已知条件代入,求出待定系数化为一般式.
3.已知二次函数 图象上的_________个点的坐标,则设一般式(即:y=________),将已知条件代入,求出 a,b,c 的值.
4.若已知抛物线与 x 轴两个交点的坐标,可设交点式(即:y=_______),求解方便.
合作探究
探究 1:长方形的周长为 20 cm,设它的一边长为 x cm,面积为 y .y 随 x 的变化而变化的规律是什么?你能分别用函数表达式、表格和图象表示出来吗?
思考:(1)用函数表达式表示:y=_____________.
(2)用表格表示:
合作探究
(3)在如图所示的平面直角坐标系中用图象表示:
(4)在上述问题中,自变量 x 的取值范围是_________.
(5)当 x 取_______时,长方形的面积最大,它的最大面积是____. 你是怎样得到的?请描述一下 y 随 x 变化的情况.
合作探究
(6)填表:
合作探究
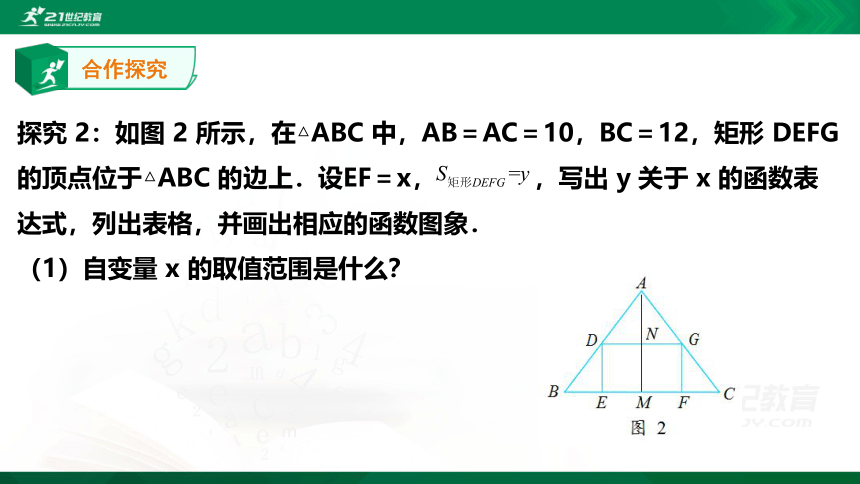
探究 2:如图 2 所示,在△ABC 中,AB=AC=10,BC=12,矩形 DEFG 的顶点位于△ABC 的边上.设EF=x, ,写出 y 关于 x 的函数表达式,列出表格,并画出相应的函数图象.
(1)自变量 x 的取值范围是什么?
合作探究
(2)图象的对称轴和顶点坐标分别是什么?
(3)如何描述 y 随 x 变化而变化的情况?
典例精讲
类型之一 求二次函数的表达式
【例 1】已知二次函数的图象经过点(0,-1),(-2,0), ,求这个二次函数的关系式.
解析:设二次函数关系式为
把点(0,-1)代入得,-a=-1,
∴a=1,
∴二次函数关系式为 .
典例精讲
类型之二 用三种不同方式表示二次函数关系
【例 2】行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离后才停止,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过 130 km/h),对这种汽车进行测试,测得数据如下表:
典例精讲
(1)以车速为 x 轴,刹车距离为 y 轴,建立坐标系,描出这些数据所表示的点,并用平滑曲线连接这些点,得到函数的大致图象;
(2)观察图象,估计该函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现测得刹车距离为 26.4 m,问在事故发生时,汽车是超速行驶还是正常行驶?请说明理由.
典例精讲
解析:(1)图略;
(2)设抛物线的解析式为
由题意得,
解得a=0.001,b=0.1,c=0,
故函数的解析式为:
(3)当y=26.4时,
典例精讲
解得: (舍去), .
∵120<130,
∴推测刹车时的速度是120 km/h,汽车是正常行驶.
课堂操练
1.若 ,则由表格中信息可知 y 与 x 之间的函数关系式是
( )
A
课堂操练
2.将抛物线 绕着它与 y 轴的交点旋转 180°,所得抛物线的解析式是( )
3.已知二次函数 的图象过点 A(1,0),且关于直线 x=2 对称,则这个二次函数的函数表达式是______________________.
B
课堂操练
4.已知二次函数 过(-1,0),(3,0), ,求此抛物线的表达式.(要求:选择除一般式求解外的方法)
解析:设所求抛物线的表达式为
∵抛物线与x轴交于(-1,0)和(3,0)两点,
∴抛物线的表达式为y=a(x+1)(x-3).
又∵抛物线过点 ,
∴a(0+1)(0-3)= ,即a=- .
课堂操练
∴y=
中考在线
(黑龙江)如图所示,在平面直角坐标系中,抛物线 与 x 轴交于点 A(3,0)点 B(-1,0),与 y轴交于点 C.
(1)求拋物线的解析式;
(2)过点 D(0,3)作直线 MN∥x 轴,点 P 在直线 NN 上且
,直接写出点 P 的坐标
中考在线
解析:(1)将点A(3,0)、点B(-1,0)代入 ,可得b=-2,c=-3,
(2)∵C(0,-3),
设P(x,3),直线CP与x轴交点为Q,
则 ,∴AQ=1,
∴Q(2,0)或Q(4,0),
中考在线
∴直线CQ为
当y=3时,x=4或x=8,
∴P(4,3)或P(8,3);
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第14课时 确定二次函数的表达式
北师大版 九年级下册
温故知新
1.解二元一次方程组(或三元一次方程组)有哪些基本方法?
2.什么叫待定系数法?
3.二次函数有哪几种基本形式?与你的小伙伴互相交流.
阅读感知
阅读课本 42~45 页,完成下面的填空:
1.确定二次函数的表达式需要_________个或________个条件.
2.确定二次函数的表达式一般用_________法求解,对不同的已知条件,应灵活设出二次函数的表达形式求解.
(1)在二次函数的各项系数中,若有两个是________的,一个是已知的,即知道图象上_______点的坐标,将两个点的坐标代入,求出两个未知数系数即可求出表达式.
阅读感知
(2)若已知二次函数的_________坐标及图象上另外一点,则可设顶点式(即:y=_________),将已知条件代入,求出待定系数化为一般式.
3.已知二次函数 图象上的_________个点的坐标,则设一般式(即:y=________),将已知条件代入,求出 a,b,c 的值.
4.若已知抛物线与 x 轴两个交点的坐标,可设交点式(即:y=_______),求解方便.
合作探究
探究 1:长方形的周长为 20 cm,设它的一边长为 x cm,面积为 y .y 随 x 的变化而变化的规律是什么?你能分别用函数表达式、表格和图象表示出来吗?
思考:(1)用函数表达式表示:y=_____________.
(2)用表格表示:
合作探究
(3)在如图所示的平面直角坐标系中用图象表示:
(4)在上述问题中,自变量 x 的取值范围是_________.
(5)当 x 取_______时,长方形的面积最大,它的最大面积是____. 你是怎样得到的?请描述一下 y 随 x 变化的情况.
合作探究
(6)填表:
合作探究
探究 2:如图 2 所示,在△ABC 中,AB=AC=10,BC=12,矩形 DEFG 的顶点位于△ABC 的边上.设EF=x, ,写出 y 关于 x 的函数表达式,列出表格,并画出相应的函数图象.
(1)自变量 x 的取值范围是什么?
合作探究
(2)图象的对称轴和顶点坐标分别是什么?
(3)如何描述 y 随 x 变化而变化的情况?
典例精讲
类型之一 求二次函数的表达式
【例 1】已知二次函数的图象经过点(0,-1),(-2,0), ,求这个二次函数的关系式.
解析:设二次函数关系式为
把点(0,-1)代入得,-a=-1,
∴a=1,
∴二次函数关系式为 .
典例精讲
类型之二 用三种不同方式表示二次函数关系
【例 2】行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离后才停止,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过 130 km/h),对这种汽车进行测试,测得数据如下表:
典例精讲
(1)以车速为 x 轴,刹车距离为 y 轴,建立坐标系,描出这些数据所表示的点,并用平滑曲线连接这些点,得到函数的大致图象;
(2)观察图象,估计该函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现测得刹车距离为 26.4 m,问在事故发生时,汽车是超速行驶还是正常行驶?请说明理由.
典例精讲
解析:(1)图略;
(2)设抛物线的解析式为
由题意得,
解得a=0.001,b=0.1,c=0,
故函数的解析式为:
(3)当y=26.4时,
典例精讲
解得: (舍去), .
∵120<130,
∴推测刹车时的速度是120 km/h,汽车是正常行驶.
课堂操练
1.若 ,则由表格中信息可知 y 与 x 之间的函数关系式是
( )
A
课堂操练
2.将抛物线 绕着它与 y 轴的交点旋转 180°,所得抛物线的解析式是( )
3.已知二次函数 的图象过点 A(1,0),且关于直线 x=2 对称,则这个二次函数的函数表达式是______________________.
B
课堂操练
4.已知二次函数 过(-1,0),(3,0), ,求此抛物线的表达式.(要求:选择除一般式求解外的方法)
解析:设所求抛物线的表达式为
∵抛物线与x轴交于(-1,0)和(3,0)两点,
∴抛物线的表达式为y=a(x+1)(x-3).
又∵抛物线过点 ,
∴a(0+1)(0-3)= ,即a=- .
课堂操练
∴y=
中考在线
(黑龙江)如图所示,在平面直角坐标系中,抛物线 与 x 轴交于点 A(3,0)点 B(-1,0),与 y轴交于点 C.
(1)求拋物线的解析式;
(2)过点 D(0,3)作直线 MN∥x 轴,点 P 在直线 NN 上且
,直接写出点 P 的坐标
中考在线
解析:(1)将点A(3,0)、点B(-1,0)代入 ,可得b=-2,c=-3,
(2)∵C(0,-3),
设P(x,3),直线CP与x轴交点为Q,
则 ,∴AQ=1,
∴Q(2,0)或Q(4,0),
中考在线
∴直线CQ为
当y=3时,x=4或x=8,
∴P(4,3)或P(8,3);
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
