【A典学案】圆-弧长及扇形的面积 1课时 课件(17张PPT)
文档属性
| 名称 | 【A典学案】圆-弧长及扇形的面积 1课时 课件(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览






文档简介
第三章 圆
第30课时 弧长及扇形的面积
北师大版 九年级下册
温故知新
1.⊙O 的半径为 r,则⊙O 的的周长 C=_______,面积 S=_______.
2.将 360°的圆心角 360 等分,则每一份的圆心角的度数为 _______,圆周被 _______等分,圆面被_______等分.
阅读感知
阅读课本 100~101 页的内容,完成下面的填空:
1.弧长的计算公式
在半径为 R 的圆中,n°的圆心角所对的弧长的计算公式为 l=_______.
2.扇形的面积
扇形的半径为 R,圆心角为 n°,那么扇形面积的计算公式为__________.
3.扇形的面积与弧长的关系
= ________ .其中 l 是扇形的弧长,R 为半径.
合作探究
探究 1:(1)你还记得圆周长的计算公式吗?圆的周长可以看成多少度的圆心角所对的弧长?
(2)1°的圆心角所对的弧长是多少?2°的呢?26°的呢?
合作探究
(3)你认为 n°的圆心角所对的弧长是多少?为什么?
(4)如图 1 所示,制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度).你会计算图中弧 AB 的长度吗?
合作探究
探究 2:(1)圆心角为 1°的扇形面积是 ________,圆心角为 n°的扇形的面积是 _______.
(2)如果已知扇形的圆心角为 120°,半径为 2,那么这个扇形的面积 S 是多少?
(3)扇形的面积公式由 S= ,如何变形为公式 S= ?
合作探究
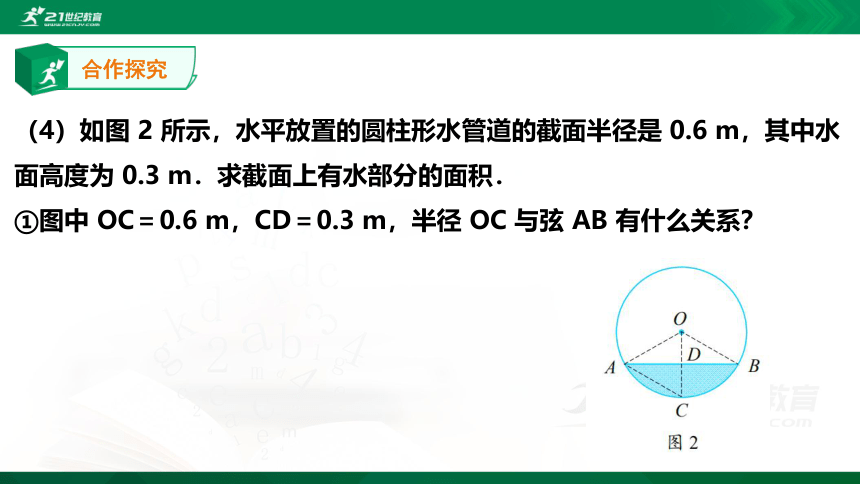
(4)如图 2 所示,水平放置的圆柱形水管道的截面半径是 0.6 m,其中水面高度为 0.3 m.求截面上有水部分的面积.
①图中 OC=0.6 m,CD=0.3 m,半径 OC 与弦 AB 有什么关系?
合作探究
②扇形 AOB 的圆心角∠AOB 的度数是多少?为什么?
③求弓形 AB 的面积方案是怎样的(即计算的关系等式)?
典例精讲
类型之一 利用弧长公式计算弧长
【例 1】如图所示是一个零件示意图,∠A,∠B,∠C 都是直角, 是圆心角为 90°的弧,其大小尺寸如图所示,求 的长.
解析: 所在圆的半径为r=7-3=4,
的长为: ×2πr=2π.
典例精讲
类型之二 利用扇形面积公式进行计算
【例 2】如图所示是某工件形状,圆弧 BC 的度数为 60°,AB=6 cm,点 B 到点 C 的距离等于 AB,∠BAC=30°,求工件的面积.
解析:在⊙O中,∵弧BC的度数为60°,
∴∠BOC=60°,△BOC是等边三角形,
∵∠BAC=30°,
∴点A也在⊙O上,
∵AB=BC,
典例精讲
∴△ABO是等边三角形,
∴∠AOB=∠OBC=60°,
∴BC∥AO,∴
∴工件的面积等于=
课堂操练
1.圆心角为 90°,半径为 R 的弧长为( )
2.如图所示,秋千拉绳长 3 米,静止时踩板离地面 0.5 米,某小朋友荡秋千时,秋千在最高处踩板离地面2 米(左右对称),则该秋千所荡过的圆弧长为( )
A
B
课堂操练
3.某花园内有一块五边形的空地如图所示,为了美化环境,现计划在以五边形各顶点为圆心,2 m 长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是( )
A.6π B.5π C.4π D.3π
A
课堂操练
4.如图所示,已知在扇形 AOB 中,若∠AOB=45°,AD=4 cm, =3π cm,则图中阴影部分的面积是 __________ .
14π
课堂操练
5.如图所示,∠AOB=90°,∠B=20°,以点 O 为圆心,OA 长为半径的圆交 AB 于点 C,若 AO=12,求 的长.
解析:连接OC,
∵∠AOB=90°,∠B=20°,
∴∠A=180°-∠AOB-∠B=70°.
∵OC=OA,
∴∠OCA=∠A=70°,
∴∠AOC=180°-2×70°=40°.
中考在线
1.(泰安)如图所示,将⊙O 沿弦 AB 折叠, 恰好经过圆心 O,若⊙O 的半径为 3,则 的长为( )
A.
B.π
C.2π
D.3π
C
中考在线
2.(南充)如图所示,在半径为 6 的⊙O 中,点 A,B,C 都在⊙O 上,四边形 OABC 是平行四边形,则图中阴影部分的面积为( )
A.6π
B.
C.
D.2π
A
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第30课时 弧长及扇形的面积
北师大版 九年级下册
温故知新
1.⊙O 的半径为 r,则⊙O 的的周长 C=_______,面积 S=_______.
2.将 360°的圆心角 360 等分,则每一份的圆心角的度数为 _______,圆周被 _______等分,圆面被_______等分.
阅读感知
阅读课本 100~101 页的内容,完成下面的填空:
1.弧长的计算公式
在半径为 R 的圆中,n°的圆心角所对的弧长的计算公式为 l=_______.
2.扇形的面积
扇形的半径为 R,圆心角为 n°,那么扇形面积的计算公式为__________.
3.扇形的面积与弧长的关系
= ________ .其中 l 是扇形的弧长,R 为半径.
合作探究
探究 1:(1)你还记得圆周长的计算公式吗?圆的周长可以看成多少度的圆心角所对的弧长?
(2)1°的圆心角所对的弧长是多少?2°的呢?26°的呢?
合作探究
(3)你认为 n°的圆心角所对的弧长是多少?为什么?
(4)如图 1 所示,制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度).你会计算图中弧 AB 的长度吗?
合作探究
探究 2:(1)圆心角为 1°的扇形面积是 ________,圆心角为 n°的扇形的面积是 _______.
(2)如果已知扇形的圆心角为 120°,半径为 2,那么这个扇形的面积 S 是多少?
(3)扇形的面积公式由 S= ,如何变形为公式 S= ?
合作探究
(4)如图 2 所示,水平放置的圆柱形水管道的截面半径是 0.6 m,其中水面高度为 0.3 m.求截面上有水部分的面积.
①图中 OC=0.6 m,CD=0.3 m,半径 OC 与弦 AB 有什么关系?
合作探究
②扇形 AOB 的圆心角∠AOB 的度数是多少?为什么?
③求弓形 AB 的面积方案是怎样的(即计算的关系等式)?
典例精讲
类型之一 利用弧长公式计算弧长
【例 1】如图所示是一个零件示意图,∠A,∠B,∠C 都是直角, 是圆心角为 90°的弧,其大小尺寸如图所示,求 的长.
解析: 所在圆的半径为r=7-3=4,
的长为: ×2πr=2π.
典例精讲
类型之二 利用扇形面积公式进行计算
【例 2】如图所示是某工件形状,圆弧 BC 的度数为 60°,AB=6 cm,点 B 到点 C 的距离等于 AB,∠BAC=30°,求工件的面积.
解析:在⊙O中,∵弧BC的度数为60°,
∴∠BOC=60°,△BOC是等边三角形,
∵∠BAC=30°,
∴点A也在⊙O上,
∵AB=BC,
典例精讲
∴△ABO是等边三角形,
∴∠AOB=∠OBC=60°,
∴BC∥AO,∴
∴工件的面积等于=
课堂操练
1.圆心角为 90°,半径为 R 的弧长为( )
2.如图所示,秋千拉绳长 3 米,静止时踩板离地面 0.5 米,某小朋友荡秋千时,秋千在最高处踩板离地面2 米(左右对称),则该秋千所荡过的圆弧长为( )
A
B
课堂操练
3.某花园内有一块五边形的空地如图所示,为了美化环境,现计划在以五边形各顶点为圆心,2 m 长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是( )
A.6π B.5π C.4π D.3π
A
课堂操练
4.如图所示,已知在扇形 AOB 中,若∠AOB=45°,AD=4 cm, =3π cm,则图中阴影部分的面积是 __________ .
14π
课堂操练
5.如图所示,∠AOB=90°,∠B=20°,以点 O 为圆心,OA 长为半径的圆交 AB 于点 C,若 AO=12,求 的长.
解析:连接OC,
∵∠AOB=90°,∠B=20°,
∴∠A=180°-∠AOB-∠B=70°.
∵OC=OA,
∴∠OCA=∠A=70°,
∴∠AOC=180°-2×70°=40°.
中考在线
1.(泰安)如图所示,将⊙O 沿弦 AB 折叠, 恰好经过圆心 O,若⊙O 的半径为 3,则 的长为( )
A.
B.π
C.2π
D.3π
C
中考在线
2.(南充)如图所示,在半径为 6 的⊙O 中,点 A,B,C 都在⊙O 上,四边形 OABC 是平行四边形,则图中阴影部分的面积为( )
A.6π
B.
C.
D.2π
A
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
