【A典学案】圆-切线长定理 1课时(18张PPT)
文档属性
| 名称 | 【A典学案】圆-切线长定理 1课时(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览







文档简介
第三章 圆
第28课时 切线长定理
北师大版 九年级下册
温故知新
1.角平分线的性质:角平分线上任意一点到角两边的距离_________.
2.三角形的外接圆及外心:经过三角形三个顶点的圆叫做________,三角形的外心是三角形的三条的交点,它到三角形三个顶点的距离_________.
切线的性质定理:圆的切线________于过切点的半经
阅读感知
阅读课本 94~95 页的内容,思考并填空:
1.经过圆外一点作圆的切线,这点和切点之间的线段的长度,叫做这点到圆的______.切线长是指一条线段的长度,这条线段的端点是________,而圆的切线是________,它是无限长的.
2.经过圆上一点可以作______ 条切线,而经过圆外的一点,可以作_____条切线.
合作探究
探究 1:如图 1 所示,过⊙O 外一点 P,引圆的切线 PA,PB,切点分别为 A,B.因为直线 OP 是⊙O 的_______,把图形沿直线 OP 对折后,点 A 与点 B 重合,此时 PB=_____,∠1=_____,△ABP 的形状是_______.
由此我们得到切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平方两条切线的夹角.
和小伙伴讨论:在图 1 中,你还能得到哪些结论?
合作探究
探究 2:如图 2 所示,△ABC 的内切圆⊙O 与 BC,CA,AB 分别相切于点 D,E,F,且 AB=9 cm,BC=14 cm,CA=13 cm,求 AF,BD,CE 的长.
合作讨论:
(1)图中除的半径相等外,还有哪些相等的线段?
(2)若设 AF=x cm,则 BF=____,BD=____,CD=____.
解:
因此,AF,BD,CE 的长分别是 _________.
典例精讲
类型之一 利用切线长定理进行计算
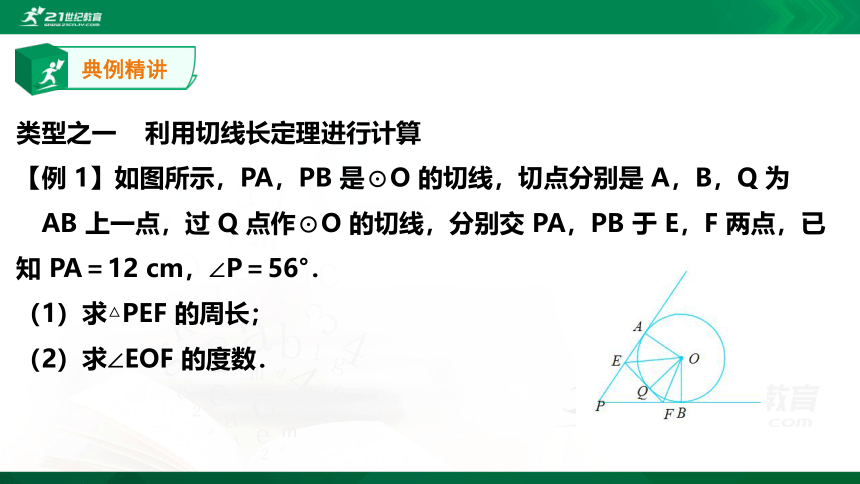
【例 1】如图所示,PA,PB 是⊙O 的切线,切点分别是 A,B,Q 为 ?AB 上一点,过 Q 点作⊙O 的切线,分别交 PA,PB 于 E,F 两点,已知 PA=12 cm,∠P=56°.
(1)求△PEF 的周长;
(2)求∠EOF 的度数.
典例精讲
解析:(1)∵PA,PB是⊙O的切线,
过点Q作⊙O的切线,PA=12 cm,
∴EA=EQ,FQ=FB,PA=PB=12 cm,
∴△PEF的周长=PE+EQ+FQ+PF=PA+PB=24 cm;
(2)∵PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°.
∵∠P=56°,∴∠AOB=124°.
∵PA,PB是⊙O的切线,过点Q作⊙O的切线,
典例精讲
∴∠EAO=∠EQO=90°,∠FQO=∠FBO=90°,
∵EA=EQ,OE=OE,∴Rt△EAO≌Rt△EQO,
∴∠AOE=∠QOE.
同理可得∠QOF=∠FOB,
∴∠EOF= ∠AOB=62°.
典例精讲
类型之二 利用切线长定理进行证明
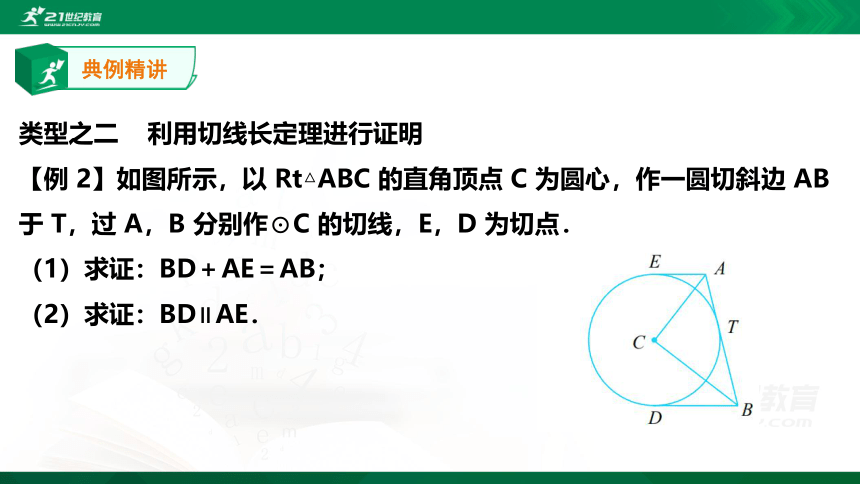
【例 2】如图所示,以 Rt△ABC 的直角顶点 C 为圆心,作一圆切斜边 AB 于 T,过 A,B 分别作⊙C 的切线,E,D 为切点.
(1)求证:BD+AE=AB;
(2)求证:BD∥AE.
典例精讲
解析:(1)∵AE,AT分别是⊙C的切线,
∴AE=AT,同理可得BD=BT,
∵BT+AT=AB,
∴BD+AE=AB;
(2)提示:∠CAB+∠CBA=90°,
∠EAB+∠DBA=180°,BD∥AE.
典例精讲
类型之三 三角形的内切圆的有关计算
【例 3】如图所示,△ABC 中,AB=AC,∠A 为锐角,CD 为 AB 上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )
A.120°
B.125°
C.135°
D.150°
C
课堂操练
1.一个钢管放在 V 形架内(如图所示),O 为钢管的圆心.如果钢管的半径为 25 cm,∠MPN=60度,则OP=( )
A
课堂操练
2.如图所示,△ABC 与⊙O 分别切于点 D,E,F,DE∥BC,AB=8,AD=5,则 BC 的长为( )
A.3 B.6 C.5 D.无法求出
B
课堂操练
3.如图所示,AC,BC 分别与⊙O 相切,∠C=80°,则∠D=____________.
4.斜边为 26 的直角三角形的内切圆的半径为 4,则此直角三角形的周长为 ___________.
50°
60
课堂操练
5.如图所示,PA,PB 是⊙O 的两条切线,A,B 为切点.求证:∠ABO=
∠APB
解析:连接OP,
∵PA,PB均为⊙O的切线,A和B是切点,
∴∠APO=∠BPO,OB⊥BP,PA=PB.
∴∠APB=2∠BPO,∠OBP=90°,PO⊥AB.
∴∠ABO+∠BOP=90°,∠BOP+∠BPO=90°.
∴∠ABO=∠BPO.∴∠ABO= ∠APB.
中考在线
(资阳)如图所示,AC 是⊙O 的直径,PA 切⊙O 于点 A,PB 切⊙O 于点 B,且∠APB=60°.
(1)求∠BAC 的度数;
(2)若 PA=1,求点 O 到弦 AB 的距离.
中考在线
解析:(1)∵PA切⊙O于点A,PB切⊙O于点B,
∴PA=PB,∠PAC=90°,
∵∠APB=60°,∴△APB是等边三角形,
∴∠BAP=60°,
∴∠BAC=90°-∠BAP=30°;
(2)作OD⊥AB于D,
则AD=BD= AB,
中考在线
由(1)得:△APB是等边三角形,
∴AB=PA=1,∴AD= ,
∵∠BAC=30°,∴AD=
即求点O到弦AB的距离为
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第28课时 切线长定理
北师大版 九年级下册
温故知新
1.角平分线的性质:角平分线上任意一点到角两边的距离_________.
2.三角形的外接圆及外心:经过三角形三个顶点的圆叫做________,三角形的外心是三角形的三条的交点,它到三角形三个顶点的距离_________.
切线的性质定理:圆的切线________于过切点的半经
阅读感知
阅读课本 94~95 页的内容,思考并填空:
1.经过圆外一点作圆的切线,这点和切点之间的线段的长度,叫做这点到圆的______.切线长是指一条线段的长度,这条线段的端点是________,而圆的切线是________,它是无限长的.
2.经过圆上一点可以作______ 条切线,而经过圆外的一点,可以作_____条切线.
合作探究
探究 1:如图 1 所示,过⊙O 外一点 P,引圆的切线 PA,PB,切点分别为 A,B.因为直线 OP 是⊙O 的_______,把图形沿直线 OP 对折后,点 A 与点 B 重合,此时 PB=_____,∠1=_____,△ABP 的形状是_______.
由此我们得到切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平方两条切线的夹角.
和小伙伴讨论:在图 1 中,你还能得到哪些结论?
合作探究
探究 2:如图 2 所示,△ABC 的内切圆⊙O 与 BC,CA,AB 分别相切于点 D,E,F,且 AB=9 cm,BC=14 cm,CA=13 cm,求 AF,BD,CE 的长.
合作讨论:
(1)图中除的半径相等外,还有哪些相等的线段?
(2)若设 AF=x cm,则 BF=____,BD=____,CD=____.
解:
因此,AF,BD,CE 的长分别是 _________.
典例精讲
类型之一 利用切线长定理进行计算
【例 1】如图所示,PA,PB 是⊙O 的切线,切点分别是 A,B,Q 为 ?AB 上一点,过 Q 点作⊙O 的切线,分别交 PA,PB 于 E,F 两点,已知 PA=12 cm,∠P=56°.
(1)求△PEF 的周长;
(2)求∠EOF 的度数.
典例精讲
解析:(1)∵PA,PB是⊙O的切线,
过点Q作⊙O的切线,PA=12 cm,
∴EA=EQ,FQ=FB,PA=PB=12 cm,
∴△PEF的周长=PE+EQ+FQ+PF=PA+PB=24 cm;
(2)∵PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°.
∵∠P=56°,∴∠AOB=124°.
∵PA,PB是⊙O的切线,过点Q作⊙O的切线,
典例精讲
∴∠EAO=∠EQO=90°,∠FQO=∠FBO=90°,
∵EA=EQ,OE=OE,∴Rt△EAO≌Rt△EQO,
∴∠AOE=∠QOE.
同理可得∠QOF=∠FOB,
∴∠EOF= ∠AOB=62°.
典例精讲
类型之二 利用切线长定理进行证明
【例 2】如图所示,以 Rt△ABC 的直角顶点 C 为圆心,作一圆切斜边 AB 于 T,过 A,B 分别作⊙C 的切线,E,D 为切点.
(1)求证:BD+AE=AB;
(2)求证:BD∥AE.
典例精讲
解析:(1)∵AE,AT分别是⊙C的切线,
∴AE=AT,同理可得BD=BT,
∵BT+AT=AB,
∴BD+AE=AB;
(2)提示:∠CAB+∠CBA=90°,
∠EAB+∠DBA=180°,BD∥AE.
典例精讲
类型之三 三角形的内切圆的有关计算
【例 3】如图所示,△ABC 中,AB=AC,∠A 为锐角,CD 为 AB 上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )
A.120°
B.125°
C.135°
D.150°
C
课堂操练
1.一个钢管放在 V 形架内(如图所示),O 为钢管的圆心.如果钢管的半径为 25 cm,∠MPN=60度,则OP=( )
A
课堂操练
2.如图所示,△ABC 与⊙O 分别切于点 D,E,F,DE∥BC,AB=8,AD=5,则 BC 的长为( )
A.3 B.6 C.5 D.无法求出
B
课堂操练
3.如图所示,AC,BC 分别与⊙O 相切,∠C=80°,则∠D=____________.
4.斜边为 26 的直角三角形的内切圆的半径为 4,则此直角三角形的周长为 ___________.
50°
60
课堂操练
5.如图所示,PA,PB 是⊙O 的两条切线,A,B 为切点.求证:∠ABO=
∠APB
解析:连接OP,
∵PA,PB均为⊙O的切线,A和B是切点,
∴∠APO=∠BPO,OB⊥BP,PA=PB.
∴∠APB=2∠BPO,∠OBP=90°,PO⊥AB.
∴∠ABO+∠BOP=90°,∠BOP+∠BPO=90°.
∴∠ABO=∠BPO.∴∠ABO= ∠APB.
中考在线
(资阳)如图所示,AC 是⊙O 的直径,PA 切⊙O 于点 A,PB 切⊙O 于点 B,且∠APB=60°.
(1)求∠BAC 的度数;
(2)若 PA=1,求点 O 到弦 AB 的距离.
中考在线
解析:(1)∵PA切⊙O于点A,PB切⊙O于点B,
∴PA=PB,∠PAC=90°,
∵∠APB=60°,∴△APB是等边三角形,
∴∠BAP=60°,
∴∠BAC=90°-∠BAP=30°;
(2)作OD⊥AB于D,
则AD=BD= AB,
中考在线
由(1)得:△APB是等边三角形,
∴AB=PA=1,∴AD= ,
∵∠BAC=30°,∴AD=
即求点O到弦AB的距离为
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
