【A典学案】圆-圆内接正多边形 1课时 课件(20张PPT)
文档属性
| 名称 | 【A典学案】圆-圆内接正多边形 1课时 课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 16:51:15 | ||
图片预览








文档简介
第三章 圆
第29课时 圆内接正多边形
北师大版 九年级下册
温故知新
1.圆心角、圆周角、弧、弦之间的关系:在同圆或等圆中,一条弧所对的圆心角等于它所对的圆周角的______;在同圆或等圆中,同弧或等弧所对的圆周角______;在同圆或等圆中,相等的圆心角所对的弧 ______;所对的弦 ______.
2.各个 ______都相等,各条______都相等的多边形叫正多边形.
3.n(n≥3)边形的内角和等于______,任意多边形的外角和均为______.
4.垂径定理:垂直于弦的直径必______,并且平分弦所对的______
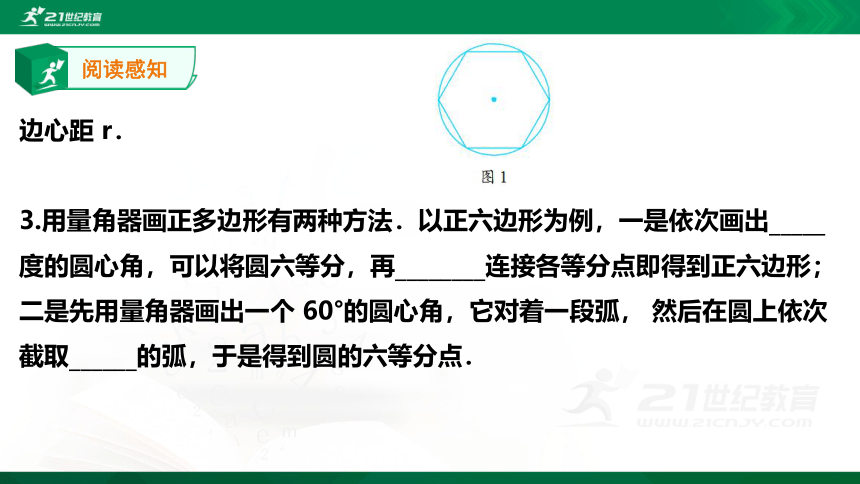
阅读感知
请同学们阅读课本第 97~98 页的内容,思考并完成下面的问题: 1.我们知道,三条边相等的三角形是正三角形,那么,各边相等的多边形就一定是正多边形吗? 只有①_____相等,②_____相等的多边形才是正多边形. 这两个条件缺一不可,
2.一个正多边形的_______的圆心叫正多边形的中心,外接圆的______叫正多边形的半径. 正多边形每一条边所对的圆心角叫正多边形的______.
中心到正多边形的一边的距离叫做正多边形的______.
请同学们在图 1 中,表示出这个六边形的中心点 O,半径 R,中心角 α,
阅读感知
边心距 r.
3.用量角器画正多边形有两种方法.以正六边形为例,一是依次画出_____度的圆心角,可以将圆六等分,再________连接各等分点即得到正六边形;二是先用量角器画出一个 60°的圆心角,它对着一段弧, 然后在圆上依次截取______的弧,于是得到圆的六等分点.
合作探究
探究 1:如图 2 所示,A,B,C,D,E 是⊙O 的五等分点,顺次连接这五个点,得到五边形.
(1)这五条边相等吗?你的依据是什么?
(2)这个五边形的五个内角相等吗?你的依据是什么?
(3)由上面的(1),(2)可知,如果将一个圆 n 等分,顺次连接各等分点,那么,得到的图形是______.
合作探究
探究 2:以图 1 的正六边形为例.
(1)正六边形的内角度数为 _____,则正 n 边形的内角度数为_____;正六边形的中心角度数为_____.则正 n 边形的中心角的度数为_____,正 n 边形的中心角与外角的大小关系是______.
(2)正六边形的半径把它分成_____个三角形,这些三角形全等吗?正 n 边形的半径、边心距与边的一半构成三角形是_____三角形,正 n 边形中,这样的三角形共有______个;
(3)正六边形有内切圆吗?其内切圆的半径与边心距的关系是______.因
合作探究
此正 n 边形的_____等于其内切圆的半径.
思考:正 n 边形是轴对称图形吗?它有______条对称轴.正多边形是是中心对称图形吗?只有边数的正多边形才是中心对称图形.
合作探究
探究 3:画一个边长为 2 cm 的正六边形.
(1)我们知道正六边形的中心角为 _______,则用量角器和圆规画正六边形有如下两种方法:
方法一:第一步:画半径为 2 cm 的⊙O,(请在图 3 中完成以下步骤);
第二步:________________________________;
第三步:________________________________.
合作探究
方法二:第一步:画半径为 2 cm 的⊙O,(请在图 4 中完成以下步骤)
第二步:________________________________;
第三步:________________________________;
第四步:________________________________.
合作探究
(2)由于正六边形的边长与其半径相等,因此,可用尺规作图.作法如下
方法三:第一步:画半径为 2 cm 的⊙O,(请在图 5 中完成以下步骤);第二步:作⊙O 的直径 AB;
第三步:分别以 A,B 为圆心,以________为半径,与圆相交于四点;
第四步:顺次连接圆上六点,即得正六边形.
合作探究
思考:(1)用尺规作出圆内接正六边形后,由此可以作出哪些正多边形?
(2)请同学们两两合作,仿照上面的三种方法依次作出正三角形、正方形和正八边形,体会以上三种方法并进行比较.
典例精讲
类型之一 证明圆内接多边形是正多边形
【例 1】如图所示,△ACD 是⊙O 的内接等腰三角形,顶角∠CAD=36°,弦 CE,DB 分别平分∠ACD,∠ADC.求证:五边形 ABCDE 为正五边形.
解析:∵AD=AC,∴∠ADC=∠ACD,
又∵∠DAC=36°,∴∠ADC=∠ACD=72°.
又∵BD,CE平分∠ADC,∠ACD,
∴∠BDC=∠BDA=∠ACE=∠ECD=∠CAD=36°,
典例精讲
∴BC=BA=AE=ED=CD,
∴五边形ABCDE为正五边形.
典例精讲
类型之二 正多边形的有关计算
【例 2】小赵对芜湖科技馆富有创意的科学方舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折,旋转放置,做成科学方舟模型,如图所示,该正五边形的边心距 OB 长 ,AC 为科学方舟船头 A 到船底的距离,请你计算 AC+ AB= _____________.(不能用三角函数表达式表示)
课堂操练
1.下列命题中,假命题的是( )
A.各边相等的圆内接多边形是正多边形
B.正多边形的任意两个角的平分线如果相交,则交点为正多边形的中心C.正多边形的任意两条边的中垂线如果相交,则交点是正多边形的中心D.一个外角小于一个内角的正多边形一定是正五边形
D
课堂操练
2.同圆的内接正四边形与外切正四边形的面积之比是( )
3.正________边形的中心角等于 18°,正十边形的一个内角等于它的中心角的________倍.
4.半径为 R 的圆内接正六边形的周长是 _________.
C
二十
四
6R
课堂操练
5.如图所示,正五边形 ABCDE 中,点 M 是 CD 的中点.求证:AM⊥CD.
解析:连接AC,AD,
∵五边形ABCDE是正五边形,
∴AB=BC=AE=ED,∠ABC=∠AED,
在△ABC和△AED中,
课堂操练
∴△ABC≌△AED(SAS),
∴AC=AD,
又M是CD的中点,
∴AM⊥CD.
中考在线
1.(雅安)如图所示,已知⊙O 的内接六边形 ABCDEF 的边心距 OM=2,则该圆的内接正△ACE 的面积为( )
A.2 B.4 C. D.
D
中考在线
2.(柳州)在半径为 5 的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为___________.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第29课时 圆内接正多边形
北师大版 九年级下册
温故知新
1.圆心角、圆周角、弧、弦之间的关系:在同圆或等圆中,一条弧所对的圆心角等于它所对的圆周角的______;在同圆或等圆中,同弧或等弧所对的圆周角______;在同圆或等圆中,相等的圆心角所对的弧 ______;所对的弦 ______.
2.各个 ______都相等,各条______都相等的多边形叫正多边形.
3.n(n≥3)边形的内角和等于______,任意多边形的外角和均为______.
4.垂径定理:垂直于弦的直径必______,并且平分弦所对的______
阅读感知
请同学们阅读课本第 97~98 页的内容,思考并完成下面的问题: 1.我们知道,三条边相等的三角形是正三角形,那么,各边相等的多边形就一定是正多边形吗? 只有①_____相等,②_____相等的多边形才是正多边形. 这两个条件缺一不可,
2.一个正多边形的_______的圆心叫正多边形的中心,外接圆的______叫正多边形的半径. 正多边形每一条边所对的圆心角叫正多边形的______.
中心到正多边形的一边的距离叫做正多边形的______.
请同学们在图 1 中,表示出这个六边形的中心点 O,半径 R,中心角 α,
阅读感知
边心距 r.
3.用量角器画正多边形有两种方法.以正六边形为例,一是依次画出_____度的圆心角,可以将圆六等分,再________连接各等分点即得到正六边形;二是先用量角器画出一个 60°的圆心角,它对着一段弧, 然后在圆上依次截取______的弧,于是得到圆的六等分点.
合作探究
探究 1:如图 2 所示,A,B,C,D,E 是⊙O 的五等分点,顺次连接这五个点,得到五边形.
(1)这五条边相等吗?你的依据是什么?
(2)这个五边形的五个内角相等吗?你的依据是什么?
(3)由上面的(1),(2)可知,如果将一个圆 n 等分,顺次连接各等分点,那么,得到的图形是______.
合作探究
探究 2:以图 1 的正六边形为例.
(1)正六边形的内角度数为 _____,则正 n 边形的内角度数为_____;正六边形的中心角度数为_____.则正 n 边形的中心角的度数为_____,正 n 边形的中心角与外角的大小关系是______.
(2)正六边形的半径把它分成_____个三角形,这些三角形全等吗?正 n 边形的半径、边心距与边的一半构成三角形是_____三角形,正 n 边形中,这样的三角形共有______个;
(3)正六边形有内切圆吗?其内切圆的半径与边心距的关系是______.因
合作探究
此正 n 边形的_____等于其内切圆的半径.
思考:正 n 边形是轴对称图形吗?它有______条对称轴.正多边形是是中心对称图形吗?只有边数的正多边形才是中心对称图形.
合作探究
探究 3:画一个边长为 2 cm 的正六边形.
(1)我们知道正六边形的中心角为 _______,则用量角器和圆规画正六边形有如下两种方法:
方法一:第一步:画半径为 2 cm 的⊙O,(请在图 3 中完成以下步骤);
第二步:________________________________;
第三步:________________________________.
合作探究
方法二:第一步:画半径为 2 cm 的⊙O,(请在图 4 中完成以下步骤)
第二步:________________________________;
第三步:________________________________;
第四步:________________________________.
合作探究
(2)由于正六边形的边长与其半径相等,因此,可用尺规作图.作法如下
方法三:第一步:画半径为 2 cm 的⊙O,(请在图 5 中完成以下步骤);第二步:作⊙O 的直径 AB;
第三步:分别以 A,B 为圆心,以________为半径,与圆相交于四点;
第四步:顺次连接圆上六点,即得正六边形.
合作探究
思考:(1)用尺规作出圆内接正六边形后,由此可以作出哪些正多边形?
(2)请同学们两两合作,仿照上面的三种方法依次作出正三角形、正方形和正八边形,体会以上三种方法并进行比较.
典例精讲
类型之一 证明圆内接多边形是正多边形
【例 1】如图所示,△ACD 是⊙O 的内接等腰三角形,顶角∠CAD=36°,弦 CE,DB 分别平分∠ACD,∠ADC.求证:五边形 ABCDE 为正五边形.
解析:∵AD=AC,∴∠ADC=∠ACD,
又∵∠DAC=36°,∴∠ADC=∠ACD=72°.
又∵BD,CE平分∠ADC,∠ACD,
∴∠BDC=∠BDA=∠ACE=∠ECD=∠CAD=36°,
典例精讲
∴BC=BA=AE=ED=CD,
∴五边形ABCDE为正五边形.
典例精讲
类型之二 正多边形的有关计算
【例 2】小赵对芜湖科技馆富有创意的科学方舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折,旋转放置,做成科学方舟模型,如图所示,该正五边形的边心距 OB 长 ,AC 为科学方舟船头 A 到船底的距离,请你计算 AC+ AB= _____________.(不能用三角函数表达式表示)
课堂操练
1.下列命题中,假命题的是( )
A.各边相等的圆内接多边形是正多边形
B.正多边形的任意两个角的平分线如果相交,则交点为正多边形的中心C.正多边形的任意两条边的中垂线如果相交,则交点是正多边形的中心D.一个外角小于一个内角的正多边形一定是正五边形
D
课堂操练
2.同圆的内接正四边形与外切正四边形的面积之比是( )
3.正________边形的中心角等于 18°,正十边形的一个内角等于它的中心角的________倍.
4.半径为 R 的圆内接正六边形的周长是 _________.
C
二十
四
6R
课堂操练
5.如图所示,正五边形 ABCDE 中,点 M 是 CD 的中点.求证:AM⊥CD.
解析:连接AC,AD,
∵五边形ABCDE是正五边形,
∴AB=BC=AE=ED,∠ABC=∠AED,
在△ABC和△AED中,
课堂操练
∴△ABC≌△AED(SAS),
∴AC=AD,
又M是CD的中点,
∴AM⊥CD.
中考在线
1.(雅安)如图所示,已知⊙O 的内接六边形 ABCDEF 的边心距 OM=2,则该圆的内接正△ACE 的面积为( )
A.2 B.4 C. D.
D
中考在线
2.(柳州)在半径为 5 的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为___________.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
