【A典学案】圆-章末复习 1课时 课件(23张PPT)
文档属性
| 名称 | 【A典学案】圆-章末复习 1课时 课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 16:55:15 | ||
图片预览







文档简介
第三章 圆
第31课时 章末复习
北师大版 九年级下册
内容分析
圆是最“完美”的几何图形,内容主要包括圆的有关概念和性质、圆中有关的角、与圆有关的位置关系、切线的判定与性质以及与圆有关的计算等.本章的重点是垂径定理、圆周角定理、圆的切线判定及性质和圆的有关计算,本章的难点是灵活运用圆的有关性质进行计算、证明和解决实际问题.
知识链接
1. 勾 股 定 理 :________.
2.全等三角形的判定方法有________ 、________、________、________、HL; 全 等 三 角 形 的 性 质 是________.
3. 相 似 三 角 形 的 判 定 方 法 有 :________ 、________ 、________;
相 似 三 角 形 的 性 质 有________.
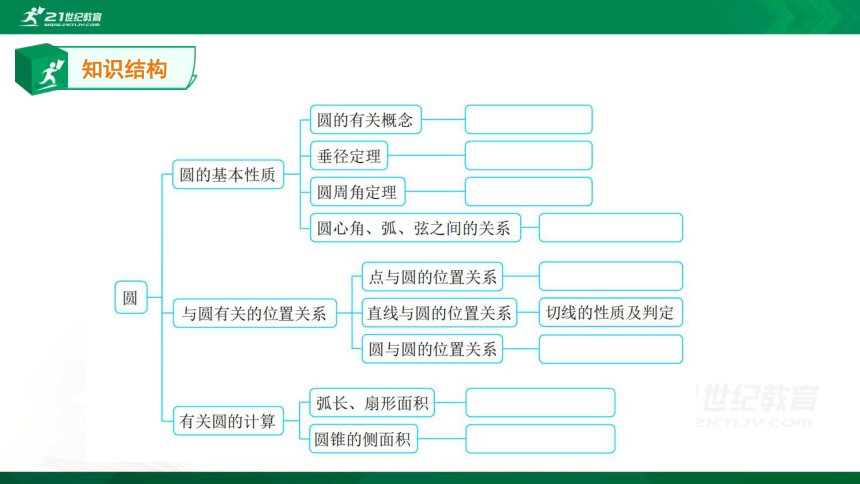
知识结构
典例精讲
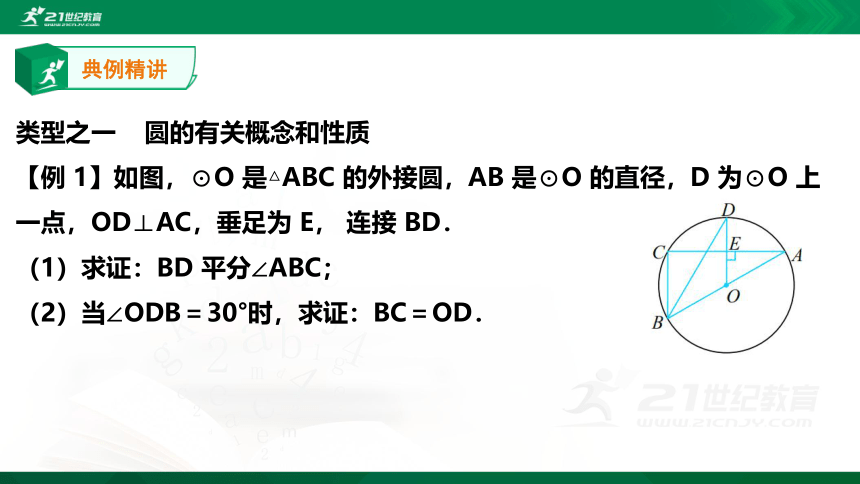
类型之一 圆的有关概念和性质
【例 1】如图,⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,D 为⊙O 上一点,OD⊥AC,垂足为 E, 连接 BD.
(1)求证:BD 平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
典例精讲
解析:(1)∵OD⊥AC,OD为半径,∴弧CD=弧AD.
∴∠CBD=∠ABD
∴BD平分∠ABC.
(2)∵OB=OD,
∴∠OBD=∠ODB=30°.
∴∠AOD=∠OBD+∠ODB=30°+30°=60°.
又∵OD⊥AC于E,
∴∠OEA=90°.
典例精讲
∴∠A=180°-∠OEA-∠AOD
=180°-90°-60°=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°.
则在Rt△ACB中,BC= AB,
∵OD= AB,
∴BC=OD.
典例精讲
类型之二 直线与圆的位置关系
【例 2】如图,已知 P 是⊙O 外一点,PO 交圆 O 于点 C,OC=CP=2,弦 AB⊥OC,劣弧 AB 所对的圆心角的度数为 120°,连接 PB.
(1)求 BC 的长;
(2)求证:PB 是⊙O 的切线.
典例精讲
解析:(1)连接OB.
∵弦AB⊥OC,劣弧AB所对的圆心角的度数为
120°,∴∠BOC=60°.
∵OB=OC,
∴△OBC是等边三角形.
典例精讲
∴BC=OC=2.
(2)证明:∵OC=CP,BC=OC,
∴BC=CP.
∴∠CBP=∠CPB.
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°.∴∠CBP=30°.
∴∠OBP=∠CBP+∠OBC=90°.∴OB⊥BP.
又∵点B在⊙O上,∴PB是⊙O的切线.
典例精讲
类型之三 弧长及扇形的面积
【例 3】如图所示,在扇形 AOB 中,∠AOB=90°,半径 OA=6.将扇形 AOB 沿过点 B 的直线折叠, 点 O 恰好落在 上点 D 处,折痕交 OA 于点 C,求整个阴影部分的周长和面积
典例精讲
解析:由折叠性质,得△BCO≌△BCD.
∴CD=CO,BD=BO=6.
∴AC+CD+BD=AC+CO+BO=AO+BO=12.
又弧AB的长为 π×6=3π,
∴阴影部分的周长为12+3π.
如图,连接OD.
∵OB=BD=OD,
∴△OBD为等边三角形.
典例精讲
∴∠DBO=60°.
∵△BCO≌△BCD.
∴∠CBO=∠CBD=30°.
∵tan 30°= ,
∴OC=OB·tan 30°=6×
课堂操练
1.如图,PA,PB 是⊙O 的切线,AC 是⊙O 的直径,∠P=50°,则∠BOC 的度数为( )
A
课堂操练
2.如图,在△ABC 中,AB=AC=10,BC=16,分别以 AB,AC 为直径作半圆,则图中阴影部分的面积是( )
A.50π-48
B.25π-48
C.50π-24
D.
B
课堂操练
3.如图所示,AM 为⊙O 的切线,A 为切点,BD⊥AM 于点 D,BD 交⊙O 于 C,OC 平分∠AOB.则∠B 的度数是__________.
60
课堂操练
4.如图所示,某小岛受到了污染,污染范围可以大致看成是以 O 为圆心,AD 为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O 的切线 BD(点 D 为切点)上选择相距 300 米的 B,C 两点,分别测得∠ABD=30°,∠ACD=60°,则直径 AD=_________米.(结果精确到 1 米)
260
课堂操练
5.如图,已知⊙O 的直径 AB 与弦 CD 互相垂直,垂足为点 E.⊙O 的切线 BF 与弦 AD 的延长线相交于点 F,且 AD=3,cos∠BCD= .
(1)求证:CD∥BF;(2)求⊙O 的半径;(3)求弦 CD 的长.
课堂操练
解析:(1)∵BF是⊙O的切线,
∴AB⊥BF.
∵AB⊥CD,
∴CD∥BF.
(2)连结BD,
∵AB是直径,
∴∠ADB=90°.
∵∠BCD=∠BAD,cos∠BCD= ,
课堂操练
∴cos∠BAD=
又∵AD=3,
∴AB=4
∴⊙O的半径为2
(3)∵cos∠DAE= ,AD=3,
∴AE=
∴ED=
CD=2ED=
中考在线
(东营)如图,AB 是⊙O 的直径,点 D 是 AB 延长线上的一点,点 C 在⊙O 上,且 AC=CD,∠ACD=120°.
(1)求证:CD 是⊙O 的切线;
(2)若⊙O 的半径为 3,求图中阴影部分的面积.
解析:(1)连接OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
中考在线
∴∠ACO=∠A=30°.
∴∠OCD=∠ACD-∠ACO=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)∵∠A=30°,∴∠COB=2∠A=60°.
∴
在Rt△OCD中,CD=OC·tan60°=
中考在线
∴图中阴影部分的面积为
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第31课时 章末复习
北师大版 九年级下册
内容分析
圆是最“完美”的几何图形,内容主要包括圆的有关概念和性质、圆中有关的角、与圆有关的位置关系、切线的判定与性质以及与圆有关的计算等.本章的重点是垂径定理、圆周角定理、圆的切线判定及性质和圆的有关计算,本章的难点是灵活运用圆的有关性质进行计算、证明和解决实际问题.
知识链接
1. 勾 股 定 理 :________.
2.全等三角形的判定方法有________ 、________、________、________、HL; 全 等 三 角 形 的 性 质 是________.
3. 相 似 三 角 形 的 判 定 方 法 有 :________ 、________ 、________;
相 似 三 角 形 的 性 质 有________.
知识结构
典例精讲
类型之一 圆的有关概念和性质
【例 1】如图,⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,D 为⊙O 上一点,OD⊥AC,垂足为 E, 连接 BD.
(1)求证:BD 平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
典例精讲
解析:(1)∵OD⊥AC,OD为半径,∴弧CD=弧AD.
∴∠CBD=∠ABD
∴BD平分∠ABC.
(2)∵OB=OD,
∴∠OBD=∠ODB=30°.
∴∠AOD=∠OBD+∠ODB=30°+30°=60°.
又∵OD⊥AC于E,
∴∠OEA=90°.
典例精讲
∴∠A=180°-∠OEA-∠AOD
=180°-90°-60°=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°.
则在Rt△ACB中,BC= AB,
∵OD= AB,
∴BC=OD.
典例精讲
类型之二 直线与圆的位置关系
【例 2】如图,已知 P 是⊙O 外一点,PO 交圆 O 于点 C,OC=CP=2,弦 AB⊥OC,劣弧 AB 所对的圆心角的度数为 120°,连接 PB.
(1)求 BC 的长;
(2)求证:PB 是⊙O 的切线.
典例精讲
解析:(1)连接OB.
∵弦AB⊥OC,劣弧AB所对的圆心角的度数为
120°,∴∠BOC=60°.
∵OB=OC,
∴△OBC是等边三角形.
典例精讲
∴BC=OC=2.
(2)证明:∵OC=CP,BC=OC,
∴BC=CP.
∴∠CBP=∠CPB.
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°.∴∠CBP=30°.
∴∠OBP=∠CBP+∠OBC=90°.∴OB⊥BP.
又∵点B在⊙O上,∴PB是⊙O的切线.
典例精讲
类型之三 弧长及扇形的面积
【例 3】如图所示,在扇形 AOB 中,∠AOB=90°,半径 OA=6.将扇形 AOB 沿过点 B 的直线折叠, 点 O 恰好落在 上点 D 处,折痕交 OA 于点 C,求整个阴影部分的周长和面积
典例精讲
解析:由折叠性质,得△BCO≌△BCD.
∴CD=CO,BD=BO=6.
∴AC+CD+BD=AC+CO+BO=AO+BO=12.
又弧AB的长为 π×6=3π,
∴阴影部分的周长为12+3π.
如图,连接OD.
∵OB=BD=OD,
∴△OBD为等边三角形.
典例精讲
∴∠DBO=60°.
∵△BCO≌△BCD.
∴∠CBO=∠CBD=30°.
∵tan 30°= ,
∴OC=OB·tan 30°=6×
课堂操练
1.如图,PA,PB 是⊙O 的切线,AC 是⊙O 的直径,∠P=50°,则∠BOC 的度数为( )
A
课堂操练
2.如图,在△ABC 中,AB=AC=10,BC=16,分别以 AB,AC 为直径作半圆,则图中阴影部分的面积是( )
A.50π-48
B.25π-48
C.50π-24
D.
B
课堂操练
3.如图所示,AM 为⊙O 的切线,A 为切点,BD⊥AM 于点 D,BD 交⊙O 于 C,OC 平分∠AOB.则∠B 的度数是__________.
60
课堂操练
4.如图所示,某小岛受到了污染,污染范围可以大致看成是以 O 为圆心,AD 为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O 的切线 BD(点 D 为切点)上选择相距 300 米的 B,C 两点,分别测得∠ABD=30°,∠ACD=60°,则直径 AD=_________米.(结果精确到 1 米)
260
课堂操练
5.如图,已知⊙O 的直径 AB 与弦 CD 互相垂直,垂足为点 E.⊙O 的切线 BF 与弦 AD 的延长线相交于点 F,且 AD=3,cos∠BCD= .
(1)求证:CD∥BF;(2)求⊙O 的半径;(3)求弦 CD 的长.
课堂操练
解析:(1)∵BF是⊙O的切线,
∴AB⊥BF.
∵AB⊥CD,
∴CD∥BF.
(2)连结BD,
∵AB是直径,
∴∠ADB=90°.
∵∠BCD=∠BAD,cos∠BCD= ,
课堂操练
∴cos∠BAD=
又∵AD=3,
∴AB=4
∴⊙O的半径为2
(3)∵cos∠DAE= ,AD=3,
∴AE=
∴ED=
CD=2ED=
中考在线
(东营)如图,AB 是⊙O 的直径,点 D 是 AB 延长线上的一点,点 C 在⊙O 上,且 AC=CD,∠ACD=120°.
(1)求证:CD 是⊙O 的切线;
(2)若⊙O 的半径为 3,求图中阴影部分的面积.
解析:(1)连接OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
中考在线
∴∠ACO=∠A=30°.
∴∠OCD=∠ACD-∠ACO=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)∵∠A=30°,∴∠COB=2∠A=60°.
∴
在Rt△OCD中,CD=OC·tan60°=
中考在线
∴图中阴影部分的面积为
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
