【A典学案】圆-直线和圆的位置关系第1课时 课件(21张PPT)
文档属性
| 名称 | 【A典学案】圆-直线和圆的位置关系第1课时 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 17:02:36 | ||
图片预览








文档简介
第三章 圆
第26课时 直线和圆的位置关系
北师大版 九年级下册
温故知新
1.点和圆有哪些位置关系?
2.类比点与圆的位置关系猜想直线和圆的位置关系.
阅读感知
阅读课本 89~90 页的内容,完成下面的填空:
1.直线和圆的位置关系
直线和圆的三种位置关系是:______、______、______.
直线和圆有唯一的公共点时,这条直线叫做圆的 ______,这个唯一的公共点叫做 ______.
2.圆心到直线的距离与半径之间的关系
设圆心 O 到直线 l 的距离为 d,圆的半径为 r,当直线和圆相交时,d ______r;当直线和圆相切时, d______r;当直线和圆相离时,d______ r.
阅读感知
3.圆的切线定理
圆的切线垂直于过______的直径.
合作探究
探究 1:在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,根据你的发现,填写下表:
合作探究
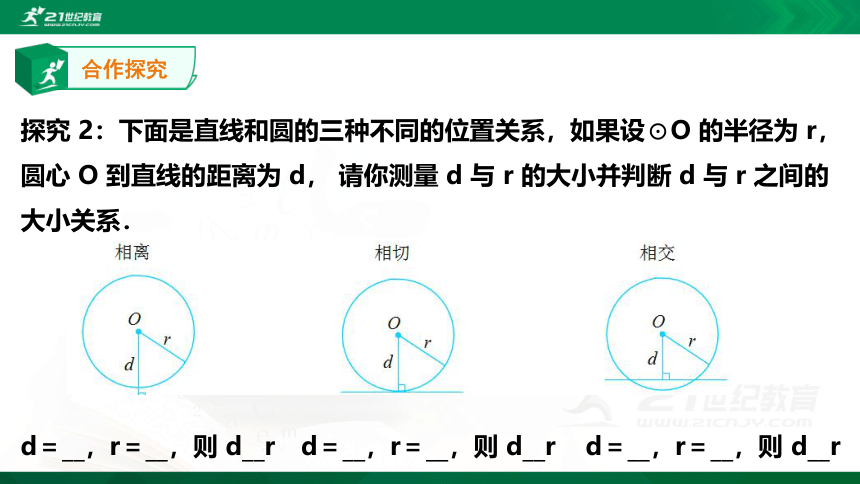
探究 2:下面是直线和圆的三种不同的位置关系,如果设⊙O 的半径为 r,圆心 O 到直线的距离为 d, 请你测量 d 与 r 的大小并判断 d 与 r 之间的大小关系.
d=__,r=__,则 d__r d=__,r=__,则 d__r d=__,r=__,则 d__r
合作探究
点和圆的位置关系可以由点与圆心的距离来决定,那么,直线和圆的三种位置关系又可以由什么来决定呢?
合作探究
探究 3:求证:圆的切线垂直于过切点的直径.
已知:如图所示,直线 CD 和⊙O 相切于点 A,AB 是⊙O 的直径.
求证:CD⊥AB.
典例精讲
类型之一 直线与圆的位置关系的判别
【例 1】已知 Rt△ABC 的斜边 AB=8 cm,AC=4 cm.
(1)以点 C 为圆心作圆,当半径为多长时,AB 与⊙O 相切?
(2)以点 C 为圆心,分别以 2 cm,4 cm 为半径作两个圆,这两个圆与直线 AB 有怎样的位置关系?
解析:(1)2 cm;
(2)r=2 cm时,⊙C与AB相离;
r=4 cm时,⊙C与AB相交.
典例精讲
类型之二 切线的性质
【例 2】如图所示,在△ABC 中,以 AB 为直径的⊙O 交 BC 与点 P,PD⊥AC 于点 D,且 PD 与⊙O 相切.
(1)求证:AB=AC;
(2)若 BC=6,AB=4,求 CD 的值.
典例精讲
解析:(1)连接OP,∵PD与⊙O相切,∴OP⊥PD,
∵AC⊥PD,∴OP∥AC,
∵OP=OA=OB= AB,∴OP是△ABC的中位线,
∴OP= AC,
∴AC=AB;
(2)连接AP,∵AB为直径,∴AP⊥BC;
由(1)知,AC=AB=4,∴PC=PB;
又∵BC=6,∴PC=3;
典例精讲
在Rt△CDP与Rt△CPA中,∠C=∠C,
∴Rt△CDP∽Rt△CPA,∴ ,
∵PC=3,AC=4,∴ .
课堂操练
1.已知⊙O 的半径为 5,圆心 O 到直线 l 的距离为 3,则反映直线 l 与⊙O 的位置关系的图形是( )
B
课堂操练
2.若 CD 是⊙O 的切线,要判定 AB⊥CD,还需添加的条件是( )
A.AB 经过圆心 O B.AB 是直径
C.AB 是直径,B 是切点 D.AB 是直线,B 是切点
3.如图所示,AB 是⊙O 的直径,O 是圆心,BC 与⊙O 相切于 B 点,CO 交⊙O 于点 D,且 BC=8,CD=4,那么⊙O 的半径是____________.
C
6
课堂操练
4.如图所示,AB 与⊙O 相切于点 B,AO 的延长线交⊙O 于点 C,连接 BC.若∠A=36°,则∠C=________.
27°
课堂操练
5.如图所示,在锐角△ABC 中,BA=BC,点 O 是边 AB 上的一个动点(不与点 A,B 重合),以 O 为圆心,OA 为半径的圆交边 AC 于点 M,过点 M 作 O 的切线 MN 交 BC 于点 N.
(1)当 OA=OB 时,求证 MN⊥BC;
(2)分别判断 OA<OB,OA>OB 时,上述结论是否成立.请选择一种情况,说明理由.
课堂操练
解析:(1)证法一:连接BC,OM.
∵AB为⊙O的直径,∴BM⊥AC.
∵BA=BC,∴M为AC的中点.
∵点O为AB的中点,∴OM∥BC.
∵MN切⊙O于中点M,∴∠OMN=90°.
∴∠MNC=∠OMN=90°,即MN⊥BC.
证法二:连接OM.∵OM=OA,∴∠A=∠OMA.
∵BA=BC,∴∠A=∠C.∴∠OMA=∠C.
课堂操练
∴OM∥BC.
∵MN切⊙O于点M,∴∠OMN=90°.
∴∠MNC=∠OMN=90°,即MN⊥BC.
(2)当OA<OB时,成立;
当OA>OB时,也成立.
以OA<OB为例证明如下.
连接OM.∵OA=OM,∴∠A=∠OMA.
∵BA=BC,∴∠A=∠C,∠OMA=∠C.
课堂操练
∴OM∥BC.
∵MN为⊙O的切线,∴∠OMN=90°.
∴∠MNC=∠OMN=90°,即MN⊥BC
中考在线
1.(嘉兴)如图所示,已知⊙O 上三点 A,B,C,半径 OC=1,∠ABC=30°,切线 PA 交 OC 延长线于点 P,则 PA 的长为( )
B
中考在线
2.(南京)如图所示,PA,PB 是⊙O 的切线,A,B 为切点,点 C,D 在⊙O 上.若∠P=102°,则∠A+∠C= ____________.
219°
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第26课时 直线和圆的位置关系
北师大版 九年级下册
温故知新
1.点和圆有哪些位置关系?
2.类比点与圆的位置关系猜想直线和圆的位置关系.
阅读感知
阅读课本 89~90 页的内容,完成下面的填空:
1.直线和圆的位置关系
直线和圆的三种位置关系是:______、______、______.
直线和圆有唯一的公共点时,这条直线叫做圆的 ______,这个唯一的公共点叫做 ______.
2.圆心到直线的距离与半径之间的关系
设圆心 O 到直线 l 的距离为 d,圆的半径为 r,当直线和圆相交时,d ______r;当直线和圆相切时, d______r;当直线和圆相离时,d______ r.
阅读感知
3.圆的切线定理
圆的切线垂直于过______的直径.
合作探究
探究 1:在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,根据你的发现,填写下表:
合作探究
探究 2:下面是直线和圆的三种不同的位置关系,如果设⊙O 的半径为 r,圆心 O 到直线的距离为 d, 请你测量 d 与 r 的大小并判断 d 与 r 之间的大小关系.
d=__,r=__,则 d__r d=__,r=__,则 d__r d=__,r=__,则 d__r
合作探究
点和圆的位置关系可以由点与圆心的距离来决定,那么,直线和圆的三种位置关系又可以由什么来决定呢?
合作探究
探究 3:求证:圆的切线垂直于过切点的直径.
已知:如图所示,直线 CD 和⊙O 相切于点 A,AB 是⊙O 的直径.
求证:CD⊥AB.
典例精讲
类型之一 直线与圆的位置关系的判别
【例 1】已知 Rt△ABC 的斜边 AB=8 cm,AC=4 cm.
(1)以点 C 为圆心作圆,当半径为多长时,AB 与⊙O 相切?
(2)以点 C 为圆心,分别以 2 cm,4 cm 为半径作两个圆,这两个圆与直线 AB 有怎样的位置关系?
解析:(1)2 cm;
(2)r=2 cm时,⊙C与AB相离;
r=4 cm时,⊙C与AB相交.
典例精讲
类型之二 切线的性质
【例 2】如图所示,在△ABC 中,以 AB 为直径的⊙O 交 BC 与点 P,PD⊥AC 于点 D,且 PD 与⊙O 相切.
(1)求证:AB=AC;
(2)若 BC=6,AB=4,求 CD 的值.
典例精讲
解析:(1)连接OP,∵PD与⊙O相切,∴OP⊥PD,
∵AC⊥PD,∴OP∥AC,
∵OP=OA=OB= AB,∴OP是△ABC的中位线,
∴OP= AC,
∴AC=AB;
(2)连接AP,∵AB为直径,∴AP⊥BC;
由(1)知,AC=AB=4,∴PC=PB;
又∵BC=6,∴PC=3;
典例精讲
在Rt△CDP与Rt△CPA中,∠C=∠C,
∴Rt△CDP∽Rt△CPA,∴ ,
∵PC=3,AC=4,∴ .
课堂操练
1.已知⊙O 的半径为 5,圆心 O 到直线 l 的距离为 3,则反映直线 l 与⊙O 的位置关系的图形是( )
B
课堂操练
2.若 CD 是⊙O 的切线,要判定 AB⊥CD,还需添加的条件是( )
A.AB 经过圆心 O B.AB 是直径
C.AB 是直径,B 是切点 D.AB 是直线,B 是切点
3.如图所示,AB 是⊙O 的直径,O 是圆心,BC 与⊙O 相切于 B 点,CO 交⊙O 于点 D,且 BC=8,CD=4,那么⊙O 的半径是____________.
C
6
课堂操练
4.如图所示,AB 与⊙O 相切于点 B,AO 的延长线交⊙O 于点 C,连接 BC.若∠A=36°,则∠C=________.
27°
课堂操练
5.如图所示,在锐角△ABC 中,BA=BC,点 O 是边 AB 上的一个动点(不与点 A,B 重合),以 O 为圆心,OA 为半径的圆交边 AC 于点 M,过点 M 作 O 的切线 MN 交 BC 于点 N.
(1)当 OA=OB 时,求证 MN⊥BC;
(2)分别判断 OA<OB,OA>OB 时,上述结论是否成立.请选择一种情况,说明理由.
课堂操练
解析:(1)证法一:连接BC,OM.
∵AB为⊙O的直径,∴BM⊥AC.
∵BA=BC,∴M为AC的中点.
∵点O为AB的中点,∴OM∥BC.
∵MN切⊙O于中点M,∴∠OMN=90°.
∴∠MNC=∠OMN=90°,即MN⊥BC.
证法二:连接OM.∵OM=OA,∴∠A=∠OMA.
∵BA=BC,∴∠A=∠C.∴∠OMA=∠C.
课堂操练
∴OM∥BC.
∵MN切⊙O于点M,∴∠OMN=90°.
∴∠MNC=∠OMN=90°,即MN⊥BC.
(2)当OA<OB时,成立;
当OA>OB时,也成立.
以OA<OB为例证明如下.
连接OM.∵OA=OM,∴∠A=∠OMA.
∵BA=BC,∴∠A=∠C,∠OMA=∠C.
课堂操练
∴OM∥BC.
∵MN为⊙O的切线,∴∠OMN=90°.
∴∠MNC=∠OMN=90°,即MN⊥BC
中考在线
1.(嘉兴)如图所示,已知⊙O 上三点 A,B,C,半径 OC=1,∠ABC=30°,切线 PA 交 OC 延长线于点 P,则 PA 的长为( )
B
中考在线
2.(南京)如图所示,PA,PB 是⊙O 的切线,A,B 为切点,点 C,D 在⊙O 上.若∠P=102°,则∠A+∠C= ____________.
219°
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
