26.1.2 第1课时 反比例函数的图象和性质(1) 课件(共28张PPT)
文档属性
| 名称 | 26.1.2 第1课时 反比例函数的图象和性质(1) 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 15:24:52 | ||
图片预览






文档简介
(共28张PPT)
第一节
反比例函数
第1课时
反比例函数的图象和性质(1)
第二十六章
反比例函数
人教版
九年级数学下册
上课课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
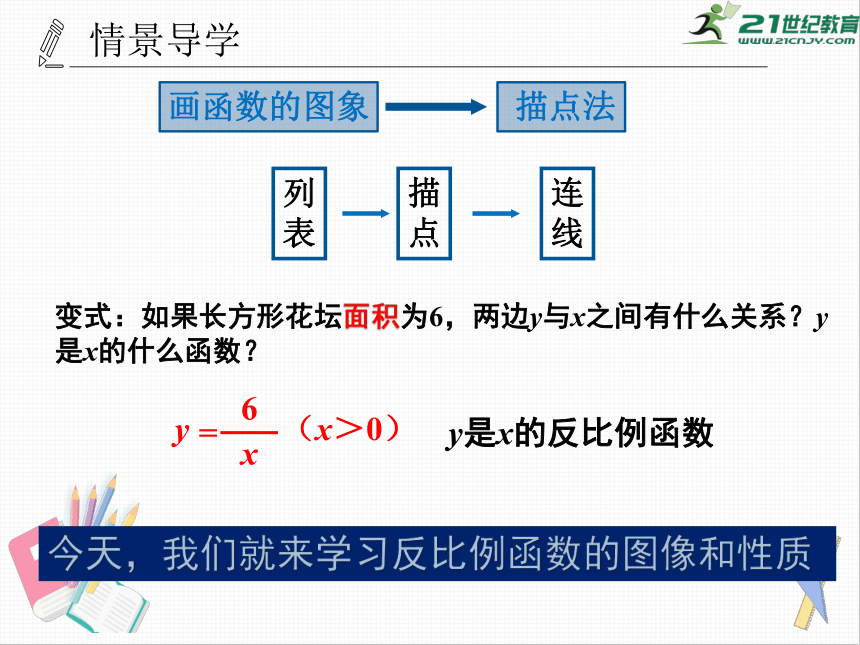
问题:如图所修建的长方形花坛一边长为6,面积y和另一边长x之间有什么关系?y是x的什么函数?
我们以前是怎样研究正比例函数y=kx(k≠0)图象和性质的?
y=6x
(x>o),y是x的正比例函数
情景导学
变式:如果长方形花坛面积为6,两边y与x之间有什么关系?y是x的什么函数?
(x>0)
列
表
描
点
连
线
描点法
画函数的图象
y是x的反比例函数
今天,我们就来学习反比例函数的图像和性质
y
6
x
=
第二部分
新课目标
新课目标
1.会用描点法画反比例函数的图象.
2.结合图象分析并掌握反比例函数的性质.
3.在画反比例函数的图象并探究其性质的过程中,体会“类比”“分类讨论”“数形结合”及“由特殊到一般”的数学思想.
教学重点:由反比例函数的图象,并结合解析式,探究反比例函数的性质.
教学难点:反比例函数图象发展趋势的理解.
第三部分
新课进行时
x
…
…
…
…
y
=
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
6
1
-1
-6
-2
-3
-3
-1.5
-2
-4
-6
-1
y
=
x
6
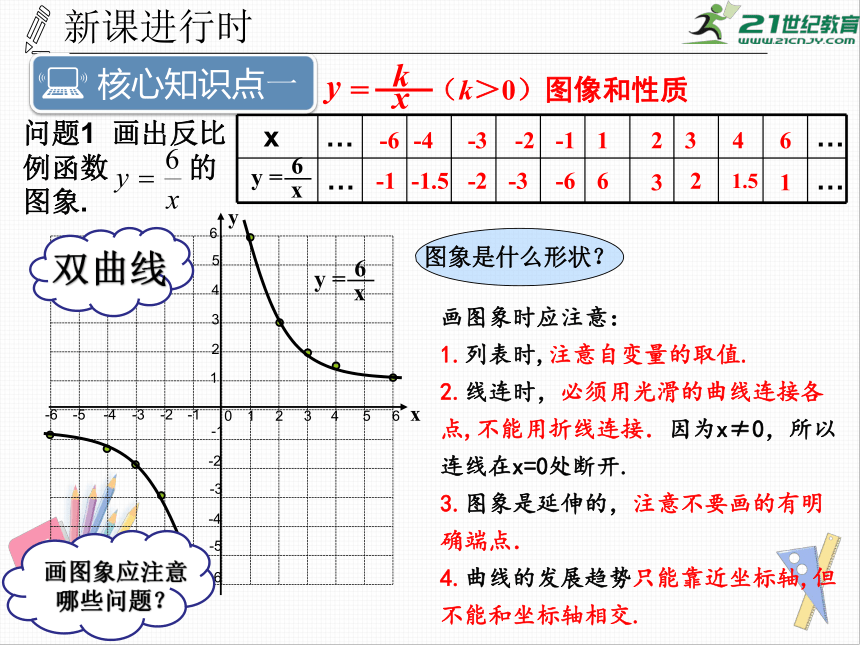
画图象时应注意:
1.列表时,注意自变量的取值.
2.线连时,必须用光滑的曲线连接各点,不能用折线连接.因为x≠0,所以连线在x=0处断开.
3.图象是延伸的,注意不要画的有明确端点.
4.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
问题1
画出反比例函数
的图象.
双曲线
图象是什么形状?
画图象应注意
哪些问题?
新课进行时
核心知识点一
y
k
x
=
(k>0)图像和性质
6
12
x
6
12
-6
-12
-6
-12
y
O
问题2
在同一坐标系内画出反比例函数
的图象
x
…
…
…
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
-1
-2
-3
-4
-6
-12
12
6
4
3
2
1
问题3
观察反比例函数
与
的图象,思考:
①它们的图象有什么共同特征?
②在每一个象限内,y随x的变化是如何变化的?
你能由它们的解析式说明理由吗?
归纳:1.反比例函数
与
的图象都有两支,分别位于第一、第三象限;2.
在每一象限内,y随x的增大而减小.
y
减
小
x
增大
新课进行时
y也为负
y也为正
x为正时
x
…
…
…
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
-1
-2
-3
-4
-6
-12
12
6
4
3
2
1
在每一象限内(每一支),
y随x的增大而减小.
y逐渐减小
x逐渐增大
x为负时
x逐渐增大
y逐渐减小
y也为正
x为正时
y也为负
x为负时
函数图象有两支
位于第一象限
位于第三象限
(+,+)
(-,-)
x≠0
新课进行时
O
x
y
对于反比例函数
(k>0),你能得到同样的性质吗?
反比例函数
(k>0)
的图象和性质:
●由两条曲线组成,且分别位于第一、三象限
,它们与
x
轴、y
轴都不相交;
●在每个象限内,y
随
x
的增大而减小.
【反思小结】由于双曲线的两个分支在两个不同的象限内,因此函数y随x的增减性就不能连续的看,一定要强调“在每一象限内”,否则,笼统说当k>0时,y随x的增大而减小,从而出现错误.
归纳
新课进行时
问题4
在同一坐标系内画出反比例函数
和
的图象.
问题5
观察图象思考:
x
y
O
6
6
-6
-6
-12
-12
12
12
1.函数图象有什么共同特征?
2.在每一象限内,y随x的变化是如何变化的?
你能由它们的解析式说明理由吗?
归纳:1.反比例函数
与
的图象有两支,分别位于第二、四象限;
2.在每一象限内,y随x的增大而增大.
新课进行时
归纳:
反比例函数图象由两条曲线组成,它是双曲线.
k>0
k<0
双曲线的两支分别位于第一、三象限
双曲线的两支分别位于第二、四象限
在每一个象限内,y随x的增大而减小
在每一个象限内,y随x的增大而增大
y
6
12
x
6
12
-6
-12
-6
O
x
y
O
6
6
-6
-6
-12
-12
12
12
k>0
k<0
新课进行时
第四部分
知识小结
函数
k的取值
图象形状
图象位置
函数值
增减规律
在每一个象限内,y随x的增大而减小
在每一个象限内,y随x的增大而增大
双曲线的两支分别位于第一、三象限
双曲线的两支分别位于第二、四象限
k>0
k<0
反比例函数的图象由两条曲线组成,它是双曲线。
数学思想:类比、分类讨论、数形结合、从特殊到一般。
知识小结
第五部分
随堂演练
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数
y
=
的图象大致是(
)
C
随堂演练
2.已知反比例函数y=
的图象过点(1,-2),则k
的值为(
)
A.2
B.-
C.1
D.-2
D
3.点
,
,
均在函数
的图象
上,则y1,y2,y3的大小关系是(
)
A.
B.
C.
D.
D
随堂演练
4.函数
的图象在第________象限,在每一象限内,y
随x
的增大而_________.
5.已知反比例函数
若函数的图象位于第一、三象限,则k_________;若在每一象限内,y随x增大而减小,则k_______.
6.若点(2,y1)、(1,y2)在反比例函数
的图
象上,则y1___
y2(填“>、<、=”)
一、三
减小
<
4
<4
<
随堂演练
7.如图所示的图象对应的函数解析式为(
)
A.y=5x
B.y=2x+3
C.
D.
变式:反比例函数为
如上题所示,则
k
0,且在图象的每一支上,y
随
x
的增大而
.
D
<
增大
随堂演练
8.已知反比例函数
的图象两个分支在二、四象限,则m的取值范围是______.
变式:若在双曲线
的一个分支上,y都随x的增大而增大,则m的取值范围是_______
m<-1
m<-1
9.已知反比例函数
在每个象限内,y
随着
x
的增大而增大,则
m
的值是____
.
-3
随堂演练
10.
已知反比例函数
的图象在第一、三象
限内,则m的取值范围是________.
11.
下列关于反比例函数
的图象的三个结论:
(1)
经过点
(-1,12)
和点
(10,-1.2);
(2)
在每一个象限内,y
随
x
的增大而减小;
(3)
双曲线位于二、四象限.
其中正确的是
(填序号).
(1)(3)
m
>
2
随堂演练
12.
已知反比例函数
y
=
mxm?-5,它的两个分支分别在第一、第三象限,求
m
的值.
解:因为反比例函数
y
=
mxm?-5
的两个分支分别在第
一、第三象限,
所以有
m2-5=-1,
m>0,
解得
m=2.
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
第一节
反比例函数
第1课时
反比例函数的图象和性质(1)
第二十六章
反比例函数
人教版
九年级数学下册
上课课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
问题:如图所修建的长方形花坛一边长为6,面积y和另一边长x之间有什么关系?y是x的什么函数?
我们以前是怎样研究正比例函数y=kx(k≠0)图象和性质的?
y=6x
(x>o),y是x的正比例函数
情景导学
变式:如果长方形花坛面积为6,两边y与x之间有什么关系?y是x的什么函数?
(x>0)
列
表
描
点
连
线
描点法
画函数的图象
y是x的反比例函数
今天,我们就来学习反比例函数的图像和性质
y
6
x
=
第二部分
新课目标
新课目标
1.会用描点法画反比例函数的图象.
2.结合图象分析并掌握反比例函数的性质.
3.在画反比例函数的图象并探究其性质的过程中,体会“类比”“分类讨论”“数形结合”及“由特殊到一般”的数学思想.
教学重点:由反比例函数的图象,并结合解析式,探究反比例函数的性质.
教学难点:反比例函数图象发展趋势的理解.
第三部分
新课进行时
x
…
…
…
…
y
=
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
6
1
-1
-6
-2
-3
-3
-1.5
-2
-4
-6
-1
y
=
x
6
画图象时应注意:
1.列表时,注意自变量的取值.
2.线连时,必须用光滑的曲线连接各点,不能用折线连接.因为x≠0,所以连线在x=0处断开.
3.图象是延伸的,注意不要画的有明确端点.
4.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
问题1
画出反比例函数
的图象.
双曲线
图象是什么形状?
画图象应注意
哪些问题?
新课进行时
核心知识点一
y
k
x
=
(k>0)图像和性质
6
12
x
6
12
-6
-12
-6
-12
y
O
问题2
在同一坐标系内画出反比例函数
的图象
x
…
…
…
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
-1
-2
-3
-4
-6
-12
12
6
4
3
2
1
问题3
观察反比例函数
与
的图象,思考:
①它们的图象有什么共同特征?
②在每一个象限内,y随x的变化是如何变化的?
你能由它们的解析式说明理由吗?
归纳:1.反比例函数
与
的图象都有两支,分别位于第一、第三象限;2.
在每一象限内,y随x的增大而减小.
y
减
小
x
增大
新课进行时
y也为负
y也为正
x为正时
x
…
…
…
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
-1
-2
-3
-4
-6
-12
12
6
4
3
2
1
在每一象限内(每一支),
y随x的增大而减小.
y逐渐减小
x逐渐增大
x为负时
x逐渐增大
y逐渐减小
y也为正
x为正时
y也为负
x为负时
函数图象有两支
位于第一象限
位于第三象限
(+,+)
(-,-)
x≠0
新课进行时
O
x
y
对于反比例函数
(k>0),你能得到同样的性质吗?
反比例函数
(k>0)
的图象和性质:
●由两条曲线组成,且分别位于第一、三象限
,它们与
x
轴、y
轴都不相交;
●在每个象限内,y
随
x
的增大而减小.
【反思小结】由于双曲线的两个分支在两个不同的象限内,因此函数y随x的增减性就不能连续的看,一定要强调“在每一象限内”,否则,笼统说当k>0时,y随x的增大而减小,从而出现错误.
归纳
新课进行时
问题4
在同一坐标系内画出反比例函数
和
的图象.
问题5
观察图象思考:
x
y
O
6
6
-6
-6
-12
-12
12
12
1.函数图象有什么共同特征?
2.在每一象限内,y随x的变化是如何变化的?
你能由它们的解析式说明理由吗?
归纳:1.反比例函数
与
的图象有两支,分别位于第二、四象限;
2.在每一象限内,y随x的增大而增大.
新课进行时
归纳:
反比例函数图象由两条曲线组成,它是双曲线.
k>0
k<0
双曲线的两支分别位于第一、三象限
双曲线的两支分别位于第二、四象限
在每一个象限内,y随x的增大而减小
在每一个象限内,y随x的增大而增大
y
6
12
x
6
12
-6
-12
-6
O
x
y
O
6
6
-6
-6
-12
-12
12
12
k>0
k<0
新课进行时
第四部分
知识小结
函数
k的取值
图象形状
图象位置
函数值
增减规律
在每一个象限内,y随x的增大而减小
在每一个象限内,y随x的增大而增大
双曲线的两支分别位于第一、三象限
双曲线的两支分别位于第二、四象限
k>0
k<0
反比例函数的图象由两条曲线组成,它是双曲线。
数学思想:类比、分类讨论、数形结合、从特殊到一般。
知识小结
第五部分
随堂演练
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数
y
=
的图象大致是(
)
C
随堂演练
2.已知反比例函数y=
的图象过点(1,-2),则k
的值为(
)
A.2
B.-
C.1
D.-2
D
3.点
,
,
均在函数
的图象
上,则y1,y2,y3的大小关系是(
)
A.
B.
C.
D.
D
随堂演练
4.函数
的图象在第________象限,在每一象限内,y
随x
的增大而_________.
5.已知反比例函数
若函数的图象位于第一、三象限,则k_________;若在每一象限内,y随x增大而减小,则k_______.
6.若点(2,y1)、(1,y2)在反比例函数
的图
象上,则y1___
y2(填“>、<、=”)
一、三
减小
<
4
<4
<
随堂演练
7.如图所示的图象对应的函数解析式为(
)
A.y=5x
B.y=2x+3
C.
D.
变式:反比例函数为
如上题所示,则
k
0,且在图象的每一支上,y
随
x
的增大而
.
D
<
增大
随堂演练
8.已知反比例函数
的图象两个分支在二、四象限,则m的取值范围是______.
变式:若在双曲线
的一个分支上,y都随x的增大而增大,则m的取值范围是_______
m<-1
m<-1
9.已知反比例函数
在每个象限内,y
随着
x
的增大而增大,则
m
的值是____
.
-3
随堂演练
10.
已知反比例函数
的图象在第一、三象
限内,则m的取值范围是________.
11.
下列关于反比例函数
的图象的三个结论:
(1)
经过点
(-1,12)
和点
(10,-1.2);
(2)
在每一个象限内,y
随
x
的增大而减小;
(3)
双曲线位于二、四象限.
其中正确的是
(填序号).
(1)(3)
m
>
2
随堂演练
12.
已知反比例函数
y
=
mxm?-5,它的两个分支分别在第一、第三象限,求
m
的值.
解:因为反比例函数
y
=
mxm?-5
的两个分支分别在第
一、第三象限,
所以有
m2-5=-1,
m>0,
解得
m=2.
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
