26.2 实际问题与反比例函数 课件(共31张PPT)
文档属性
| 名称 | 26.2 实际问题与反比例函数 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 13:39:31 | ||
图片预览









文档简介
(共31张PPT)
第二十六章
反比例函数
第二节
实际问题与反比例函数
人教版
九年级数学下册
上课课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
你吃过拉面吗?你知道在做拉面的过程中渗透着什么数学知识吗?
(1)体积为20cm3的面团做成拉面,面条的总长度y与面条粗细(横截面积)s有怎样的函数关系?
(2)某家面馆的师傅手艺精湛,他拉的面条粗1mm2,面条总长是多少?
上面的问题中,面条的总长度y是面条粗细x的反比例函数,反比例函数在实际生活中应用非常广泛,今天这节课我们就来学习反比例函数的应用.
2000
cm
情景导学
y
=
20
s
第二部分
新课目标
新课目标
1.利用反比例函数的知识分析、解决实际生活中的面(体)积问题、装卸货物问题及物理中的实际问题.
2.从实际问题中抽象出数学问题,建立函数模型,运用所学的数学知识解决实际问题.
3.掌握反比例函数在其他学科中的运用,让学生体验学科的整合思想
.
教学重点:运用反比例函数的性质解决实际问题
教学难点:构建反比例函数模型解决实际应用问题,巩固反比例函数性质.
第三部分
新课进行时
例1:市煤气公司要在地下修建一个容积为104
m3的圆柱形煤气储存室.
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积S定为500
m2,施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?
新课进行时
核心知识点一
用反比例函数解决面积、体积类问题
解:
(1)根据圆柱体的体积公式,我们有
s×d
=
变形得
即储存室的底面积S是其深度d的反比例函数.
(1)求储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系时,可以根据圆柱体的什么公式列方程再变形?
(2)公司决定把储存室的底面积S定为500
m?,施工队施工时应该向下掘进多深?实际上是已知什么条件,求什么?如何解答?
解:
把S=500代入
,得
解得
d=20
如果把储存室的底面积定为500
?,施工时应向地下掘进20m深.
s
=
104
d
104
s
=
104
d
500
=
104
d
新课进行时
根据题意,把d=15代入
,得
解得
S≈666.67
答:当储存室的深为15m时,储存室的底面积应改为666.67m2才能满足需要.
(3)求当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要时,实际上是已知什么条件,求什么?如何求?组卷网
解:
反思小结:解决实际生活中的体积问题,应先根据体积公式列出方程,再变形从而得出函数解析式,然后再结合题意中已知的两个量,求出另外一个量.
新课进行时
思考:如何应用反比例函数解决生活中的体积问题?
s
=
104
d
s
=
104
15
例2:码头工人以每天30吨的速度往
一艘轮船上装载货物,把轮船装载完
毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货
速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
(2)由于遇到紧急情况,船上的货物必须在不超过5日内卸载完毕,那么平均每天至少要卸多少吨货物?
1.如何求装载的货物的数量?装载的货物与卸载的货物有什么关系?卸载的货物的数量、卸货时间与卸货速度之间有什么关系?
2.卸货时间是5天时,每天应卸货多少?如何根据反比例函数的性质,求出在不超过5日内卸载完毕,平均每天至少的卸货量?
新课进行时
核心知识点二
用反比例函数解决工程问题
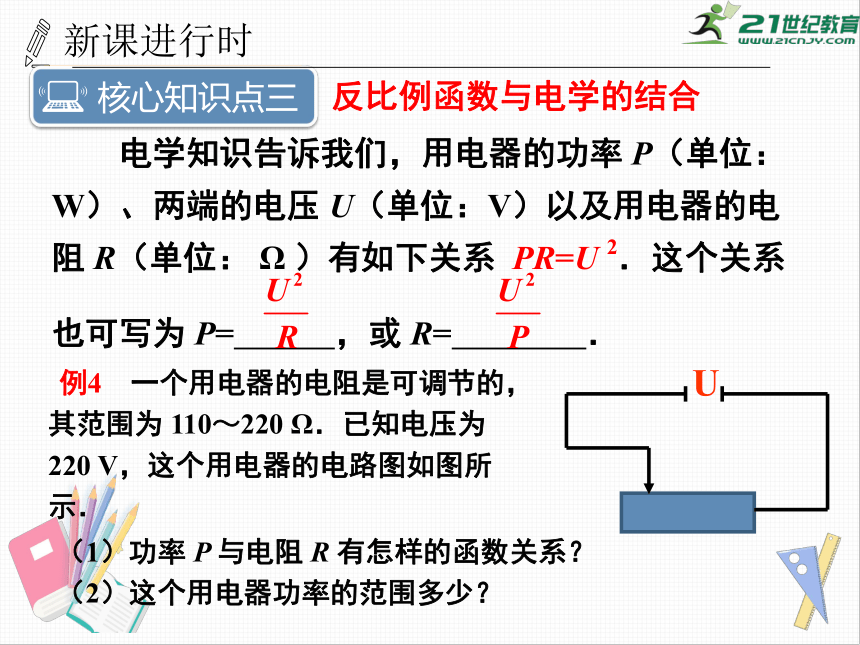
电学知识告诉我们,用电器的功率
P(单位:W)、两端的电压
U(单位:V)以及用电器的电阻
R(单位:
Ω
)有如下关系
PR=U
2.这个关系
也可写为
P= ,或
R= .
例4
一个用电器的电阻是可调节的,其范围为
110~220
Ω.已知电压为
220
V,这个用电器的电路图如图所示.
(1)功率
P
与电阻
R
有怎样的函数关系?
(2)这个用电器功率的范围多少?
U
新课进行时
核心知识点三
反比例函数与电学的结合
解:(1)根据电学知识,当
U=220
时,得
即输出功率
P
是电阻
R
的反比例函数,函数解析式
为
①
(2)根据反比例函数的性质可知,电阻越大,功率越小.把电阻的最小值
R=110
代入
①
式,得到功率的最大值
把电阻的最大值
R=220
代入
①
式,得到功率的最
小值
因此,用电器的功率为
220~440
W
.
新课进行时
阻力
动力
支点
动力臂
阻力臂
例3
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为
1
200
N
和
0.5
m.(1)动力
F
与动力臂
l
有怎样的函数关系?当动力臂为
1.5
m
时,撬动石头至少需要多大的力?(2)若想使动力
F
不超过题(1)中所用力的一半,则动力臂
l
至少要加长多少?
1.动力、动力臂与阻力、阻力臂之间有什么关系?
2.如何运用反比例函数的性质,计算要想使动力
F
不超过题(1)中所用力的一半,则动力臂
l
至少要加长的长度?
新课进行时
核心知识点四
反比例函数在力学中的应用
思考
3-1.5=1.5(m)
因此,若想用力不超过
400
N
的一半,动力臂至少要加长
1.5
m.
(2)当
F=400×0.5=200
N
时,
解:(1)根据“杠杆原理”得,
Fl
=
1
200×0.5,所以
F
关于
l
的函数解析式为
当
l
=
1.5
m
时,
新课进行时
对于函数
,当F大于0时,F
随
l
的增大而减小,即F取最大值200N时,l
有最小值3
m
结合例4,小组讨论为什么收音机的音量、某些台灯的亮度以及电风扇的转速可以调节.
因为电压一定时,电功率与电阻成反比例,改变用电器的电阻,电功率就会改变,而收音机的音量、台灯的亮度以及电风扇的转速由用电器的功率决定.
新课进行时
第四部分
知识小结
知识小结:
1.圆柱体的体积一定时,柱体的底面积与高成反比;
2.卸载货物的总量一定时,卸载时间与速度成反比例;
3.“杠杆定律”:动力×动力臂=阻力×阻力臂;
4.电压一定时,电功率与电阻成反比例.
(1)本节课你有哪些收获?还有什么困惑?
思想方法小结:建模—反比例函数的数学思想方法.
(2)建立反比例函数模型解决实际问题的过程是怎样的
?
实际问题
现实生活中的反比例函数
建立反比例函数模型
运用反比例函数图象性质
知识小结
第五部分
随堂演练
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛和0.5米,那么动力F和动力臂L之间的函数关系式是________.
2.
小强欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1000牛顿和0.5米,则当动力臂为1米时,撬动石头至少需要的力为________牛顿.
500
随堂演练
3.如图,科技小组准备用材料围建一个面积为50
m2
的矩形科技园
ABCD,其中一边
AB
靠墙,墙长为
12
m,设
AD
的长为
x
m,DC
的长为
y
m.
①求
y
与
x
之间的函数关系式;
②若围成矩形科技园
ABCD
的三边材料总长
20m,求x和y的值.
x
=
5
m,y
=
10
m
随堂演练
y
=
50
x
解:(1)由题意,S△ABC=
xy,把点(3,4)代入得S△ABC=
6,
∴y关于x的函数解析式是y=
,△ABC的面积是6厘米2;
(2)如图所示:当x=2时,y=6;当x=8时,y=1.5,
由函数y=
图象的性质得,
在第一象限y随x的增大而减小,
∴当2<x<8时,y的取值范围是1.5<y<6.
4.设?ABC中BC边的长为x(cm),BC上的高AD为y(cm).
已知y关于x的函数图象过点(3,4).
⑴求y关于x的函数解析式和?ABC
的面积.
⑵画出函数的图象,并利用图象,求当2<x<8时y的取值范围.
随堂演练
1
2
12
x
12
x
5.某项工程需要沙石料2×106立方米,阳光公司承担了该工程运送沙石料的任务.
(1)在这项任务中平均每天的工作量v(立方米/天)与完成任务所需要的时间t(天)之间具有怎样的函数关系写出这个函数关系式.
(2)阳光公司计划投入A型卡车200辆,每天一共可以运送沙石料2×104立方米,则完成全部运送任务需要多少天如果工作了25天后,由于工程进度的需要,公司准备再投入A型卡车120辆.在保持每辆车每天工作量不变的前提下,问:是否能提前28天完成任务?
解:把V=2×104代入函数式得:t=100天,每辆车每天能运送石料100(立方米),
(2×106-2×104×25)÷[(200+120)×100]=46.875(天),
因为100-25-46.875=28.125>28,所以能提前28天完成任务.
随堂演练
v
=
2×106
t
6.为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量
y(毫克)与时间
t(小时)成正比;药物释放完毕后,y
与
t
的函数关系式为
(a为常数).如图所示,据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y
与
t
之间的两个函数关系式及相应的自变量的取值范围;
解:(1)药物释放过程:
药物释放完毕后:
随堂演练
(2)据测定,当空气中每立方米的含药量降低到
0.25
毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
解:(2)当
y
=
0.25
毫克时,由
得
(小时),至少需要经过
6
小时后,学生才能进入教室.
随堂演练
7.现在要求取消市场上使用杆秤的呼声越来越高.原因在于,一些不法商贩在卖货时将秤砣挖空或更换较小秤砣,使秤砣变轻,从而欺骗顾客.
a.如图1,2所示,对于同一物体,哪个用了较轻的秤砣?
b.在称同一物体时,秤砣到支点的距离
y
与所用秤砣质量
x
之间满足__________关系;
c.当秤砣变轻时,称得的物体变重,这正好符合哪个函数的哪些性质?
反比例
随堂演练
8.
舞台灯光可以瞬间将阳光灿烂的晴天变成浓云密布的阴天,或由黑夜变成白昼,这样的效果是通过改变电阻来控制电流的变化实现的.因为当电流
I
较小时,灯光较暗;反之,当电流
I
较大时,灯光较亮.在某一舞台的电路中,保持电压不变,
电流
I(A)与电阻
R(Ω)成
反比例,当电阻R
=20
Ω时,电流
I
=11
A.
(1)求电流
I(A)与电阻
R(Ω)之间的函数关系式;
(2)当舞台线路所承受的电流不超过
10
A时,那么电阻
R
至少应该是多少?
R至少应该是22Ω
随堂演练
I
=
2×106
t
U
R
=
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
文本
文本
文本
单击此处添加文本
文本
谢谢欣赏
第二十六章
反比例函数
第二节
实际问题与反比例函数
人教版
九年级数学下册
上课课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
你吃过拉面吗?你知道在做拉面的过程中渗透着什么数学知识吗?
(1)体积为20cm3的面团做成拉面,面条的总长度y与面条粗细(横截面积)s有怎样的函数关系?
(2)某家面馆的师傅手艺精湛,他拉的面条粗1mm2,面条总长是多少?
上面的问题中,面条的总长度y是面条粗细x的反比例函数,反比例函数在实际生活中应用非常广泛,今天这节课我们就来学习反比例函数的应用.
2000
cm
情景导学
y
=
20
s
第二部分
新课目标
新课目标
1.利用反比例函数的知识分析、解决实际生活中的面(体)积问题、装卸货物问题及物理中的实际问题.
2.从实际问题中抽象出数学问题,建立函数模型,运用所学的数学知识解决实际问题.
3.掌握反比例函数在其他学科中的运用,让学生体验学科的整合思想
.
教学重点:运用反比例函数的性质解决实际问题
教学难点:构建反比例函数模型解决实际应用问题,巩固反比例函数性质.
第三部分
新课进行时
例1:市煤气公司要在地下修建一个容积为104
m3的圆柱形煤气储存室.
(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
(2)公司决定把储存室的底面积S定为500
m2,施工队施工时应该向下掘进多深?
(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?
新课进行时
核心知识点一
用反比例函数解决面积、体积类问题
解:
(1)根据圆柱体的体积公式,我们有
s×d
=
变形得
即储存室的底面积S是其深度d的反比例函数.
(1)求储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系时,可以根据圆柱体的什么公式列方程再变形?
(2)公司决定把储存室的底面积S定为500
m?,施工队施工时应该向下掘进多深?实际上是已知什么条件,求什么?如何解答?
解:
把S=500代入
,得
解得
d=20
如果把储存室的底面积定为500
?,施工时应向地下掘进20m深.
s
=
104
d
104
s
=
104
d
500
=
104
d
新课进行时
根据题意,把d=15代入
,得
解得
S≈666.67
答:当储存室的深为15m时,储存室的底面积应改为666.67m2才能满足需要.
(3)求当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要时,实际上是已知什么条件,求什么?如何求?组卷网
解:
反思小结:解决实际生活中的体积问题,应先根据体积公式列出方程,再变形从而得出函数解析式,然后再结合题意中已知的两个量,求出另外一个量.
新课进行时
思考:如何应用反比例函数解决生活中的体积问题?
s
=
104
d
s
=
104
15
例2:码头工人以每天30吨的速度往
一艘轮船上装载货物,把轮船装载完
毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货
速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
(2)由于遇到紧急情况,船上的货物必须在不超过5日内卸载完毕,那么平均每天至少要卸多少吨货物?
1.如何求装载的货物的数量?装载的货物与卸载的货物有什么关系?卸载的货物的数量、卸货时间与卸货速度之间有什么关系?
2.卸货时间是5天时,每天应卸货多少?如何根据反比例函数的性质,求出在不超过5日内卸载完毕,平均每天至少的卸货量?
新课进行时
核心知识点二
用反比例函数解决工程问题
电学知识告诉我们,用电器的功率
P(单位:W)、两端的电压
U(单位:V)以及用电器的电阻
R(单位:
Ω
)有如下关系
PR=U
2.这个关系
也可写为
P= ,或
R= .
例4
一个用电器的电阻是可调节的,其范围为
110~220
Ω.已知电压为
220
V,这个用电器的电路图如图所示.
(1)功率
P
与电阻
R
有怎样的函数关系?
(2)这个用电器功率的范围多少?
U
新课进行时
核心知识点三
反比例函数与电学的结合
解:(1)根据电学知识,当
U=220
时,得
即输出功率
P
是电阻
R
的反比例函数,函数解析式
为
①
(2)根据反比例函数的性质可知,电阻越大,功率越小.把电阻的最小值
R=110
代入
①
式,得到功率的最大值
把电阻的最大值
R=220
代入
①
式,得到功率的最
小值
因此,用电器的功率为
220~440
W
.
新课进行时
阻力
动力
支点
动力臂
阻力臂
例3
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为
1
200
N
和
0.5
m.(1)动力
F
与动力臂
l
有怎样的函数关系?当动力臂为
1.5
m
时,撬动石头至少需要多大的力?(2)若想使动力
F
不超过题(1)中所用力的一半,则动力臂
l
至少要加长多少?
1.动力、动力臂与阻力、阻力臂之间有什么关系?
2.如何运用反比例函数的性质,计算要想使动力
F
不超过题(1)中所用力的一半,则动力臂
l
至少要加长的长度?
新课进行时
核心知识点四
反比例函数在力学中的应用
思考
3-1.5=1.5(m)
因此,若想用力不超过
400
N
的一半,动力臂至少要加长
1.5
m.
(2)当
F=400×0.5=200
N
时,
解:(1)根据“杠杆原理”得,
Fl
=
1
200×0.5,所以
F
关于
l
的函数解析式为
当
l
=
1.5
m
时,
新课进行时
对于函数
,当F大于0时,F
随
l
的增大而减小,即F取最大值200N时,l
有最小值3
m
结合例4,小组讨论为什么收音机的音量、某些台灯的亮度以及电风扇的转速可以调节.
因为电压一定时,电功率与电阻成反比例,改变用电器的电阻,电功率就会改变,而收音机的音量、台灯的亮度以及电风扇的转速由用电器的功率决定.
新课进行时
第四部分
知识小结
知识小结:
1.圆柱体的体积一定时,柱体的底面积与高成反比;
2.卸载货物的总量一定时,卸载时间与速度成反比例;
3.“杠杆定律”:动力×动力臂=阻力×阻力臂;
4.电压一定时,电功率与电阻成反比例.
(1)本节课你有哪些收获?还有什么困惑?
思想方法小结:建模—反比例函数的数学思想方法.
(2)建立反比例函数模型解决实际问题的过程是怎样的
?
实际问题
现实生活中的反比例函数
建立反比例函数模型
运用反比例函数图象性质
知识小结
第五部分
随堂演练
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛和0.5米,那么动力F和动力臂L之间的函数关系式是________.
2.
小强欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1000牛顿和0.5米,则当动力臂为1米时,撬动石头至少需要的力为________牛顿.
500
随堂演练
3.如图,科技小组准备用材料围建一个面积为50
m2
的矩形科技园
ABCD,其中一边
AB
靠墙,墙长为
12
m,设
AD
的长为
x
m,DC
的长为
y
m.
①求
y
与
x
之间的函数关系式;
②若围成矩形科技园
ABCD
的三边材料总长
20m,求x和y的值.
x
=
5
m,y
=
10
m
随堂演练
y
=
50
x
解:(1)由题意,S△ABC=
xy,把点(3,4)代入得S△ABC=
6,
∴y关于x的函数解析式是y=
,△ABC的面积是6厘米2;
(2)如图所示:当x=2时,y=6;当x=8时,y=1.5,
由函数y=
图象的性质得,
在第一象限y随x的增大而减小,
∴当2<x<8时,y的取值范围是1.5<y<6.
4.设?ABC中BC边的长为x(cm),BC上的高AD为y(cm).
已知y关于x的函数图象过点(3,4).
⑴求y关于x的函数解析式和?ABC
的面积.
⑵画出函数的图象,并利用图象,求当2<x<8时y的取值范围.
随堂演练
1
2
12
x
12
x
5.某项工程需要沙石料2×106立方米,阳光公司承担了该工程运送沙石料的任务.
(1)在这项任务中平均每天的工作量v(立方米/天)与完成任务所需要的时间t(天)之间具有怎样的函数关系写出这个函数关系式.
(2)阳光公司计划投入A型卡车200辆,每天一共可以运送沙石料2×104立方米,则完成全部运送任务需要多少天如果工作了25天后,由于工程进度的需要,公司准备再投入A型卡车120辆.在保持每辆车每天工作量不变的前提下,问:是否能提前28天完成任务?
解:把V=2×104代入函数式得:t=100天,每辆车每天能运送石料100(立方米),
(2×106-2×104×25)÷[(200+120)×100]=46.875(天),
因为100-25-46.875=28.125>28,所以能提前28天完成任务.
随堂演练
v
=
2×106
t
6.为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量
y(毫克)与时间
t(小时)成正比;药物释放完毕后,y
与
t
的函数关系式为
(a为常数).如图所示,据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y
与
t
之间的两个函数关系式及相应的自变量的取值范围;
解:(1)药物释放过程:
药物释放完毕后:
随堂演练
(2)据测定,当空气中每立方米的含药量降低到
0.25
毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
解:(2)当
y
=
0.25
毫克时,由
得
(小时),至少需要经过
6
小时后,学生才能进入教室.
随堂演练
7.现在要求取消市场上使用杆秤的呼声越来越高.原因在于,一些不法商贩在卖货时将秤砣挖空或更换较小秤砣,使秤砣变轻,从而欺骗顾客.
a.如图1,2所示,对于同一物体,哪个用了较轻的秤砣?
b.在称同一物体时,秤砣到支点的距离
y
与所用秤砣质量
x
之间满足__________关系;
c.当秤砣变轻时,称得的物体变重,这正好符合哪个函数的哪些性质?
反比例
随堂演练
8.
舞台灯光可以瞬间将阳光灿烂的晴天变成浓云密布的阴天,或由黑夜变成白昼,这样的效果是通过改变电阻来控制电流的变化实现的.因为当电流
I
较小时,灯光较暗;反之,当电流
I
较大时,灯光较亮.在某一舞台的电路中,保持电压不变,
电流
I(A)与电阻
R(Ω)成
反比例,当电阻R
=20
Ω时,电流
I
=11
A.
(1)求电流
I(A)与电阻
R(Ω)之间的函数关系式;
(2)当舞台线路所承受的电流不超过
10
A时,那么电阻
R
至少应该是多少?
R至少应该是22Ω
随堂演练
I
=
2×106
t
U
R
=
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
文本
文本
文本
单击此处添加文本
文本
谢谢欣赏
