26.3 第1课时 运用二次函数解决实际问题 课件(共41张PPT)
文档属性
| 名称 | 26.3 第1课时 运用二次函数解决实际问题 课件(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 15:37:56 | ||
图片预览




文档简介
(共41张PPT)
第二十六章
二次函数
26.3
实践与探索
第1课时
运用二次函数解决实际问题
华东师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.(重点)
2.利用二次函数解决拱桥及运动中的有关问题.
(重、难点)
3.能运用二次函数的图象与性质进行决策.
情景导学
2
情景导学
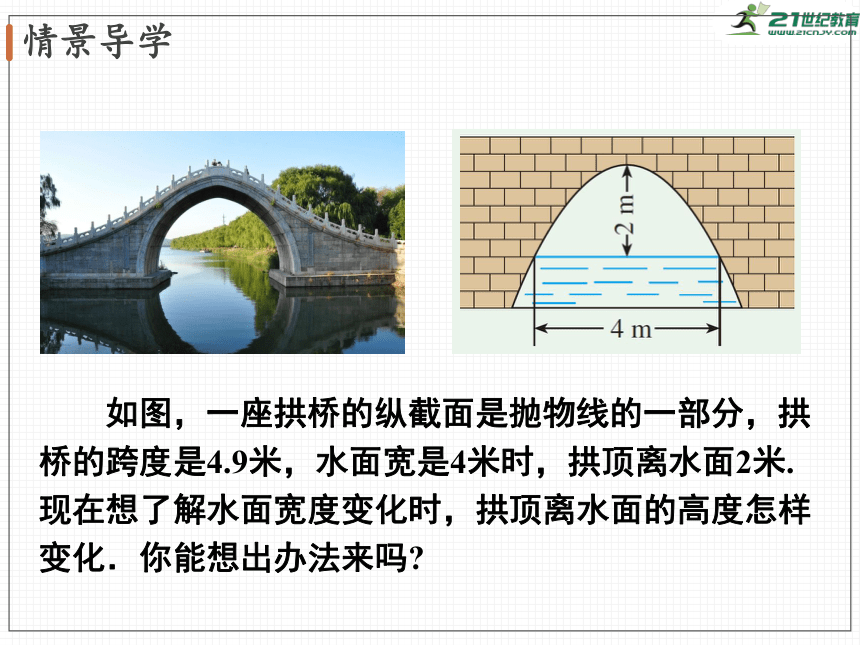
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
新课进行时
3
新课进行时
核心知识点一
利用二次函数解决实物抛物线形问题
建立函数模型
这是什么样的函数呢?
拱桥的纵截面是抛物线,所以应当是个二次函数。
你能想出办法来吗?
合作探究
新课进行时
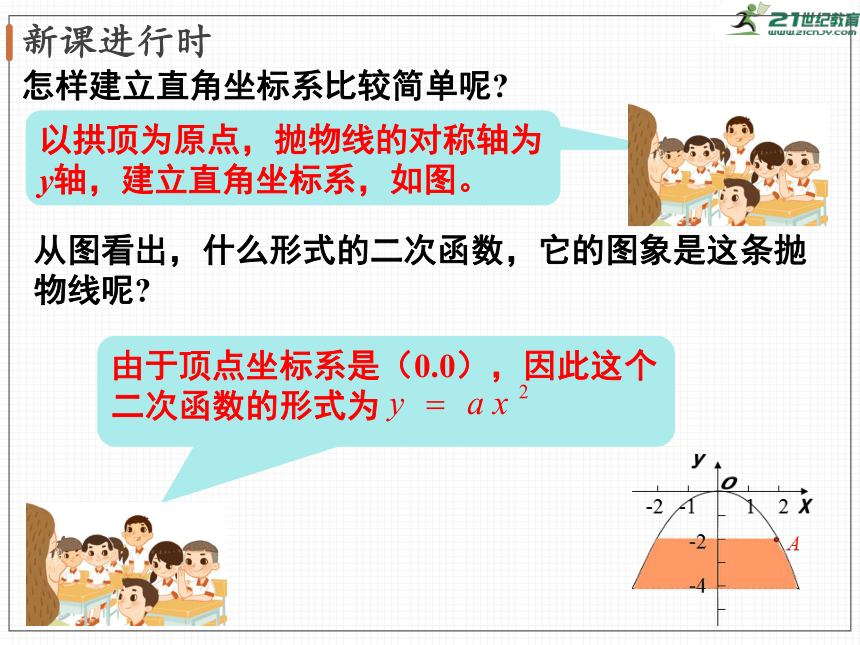
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图。
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
新课进行时
x
O
y
-2
-4
2
1
-2
-1
A
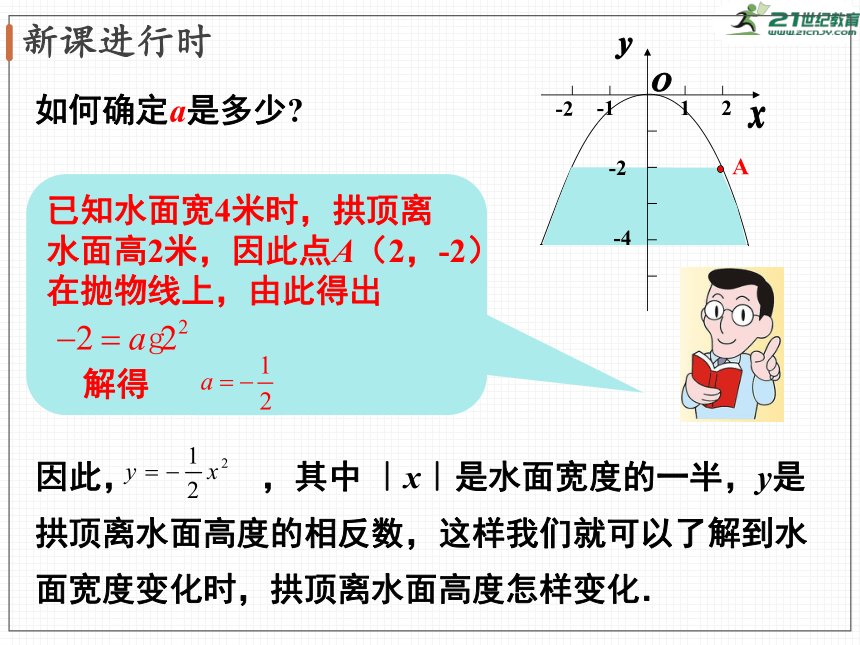
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
因此,
,其中
|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
解得
新课进行时
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时
从而
因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
新课进行时
知识要点
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的图象和性质求解
实际问题的解
新课进行时
例1
某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
典例精析
新课进行时
解:建立如图所示的坐标系,
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
●B(1,2.25)
(0,1.25)
●
C
●
D
o
A
x
y
新课进行时
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0)
;同理,点
D的坐标为(-2.5,0)
.
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=-
(x-1)2+2.25.
●B(1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
新课进行时
核心知识点二
利用二次函数解决运动中抛物线型问题
例2:如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
新课进行时
解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
新课进行时
解得
a=-0.2,
k=3.5,
设以y轴为对称轴的抛物线的解析式为
y=a(x-0)2+k
,
即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=-0.2x2+3.5.
当
x=-2.5时,y=2.25
.
故该运动员出手时的高度为2.25m.
2.25a+k=3.05,
k=3.5,
x
y
O
新课进行时
核心知识点三
拱桥问题
问题1
图中是抛物线形拱桥,当拱顶离水面
2m时,水面宽
4m
.
水面下降
1m,水面宽度增加多少?
互动探究
新课进行时
(1)求宽度增加多少需要什么数据?
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
想一想
新课进行时
问题2
如何建立直角坐标系?
l
问题3
解决本题的关键是什么?
y
x
o
解:如图建立直角坐标系.
解:建立合适的直角坐标系.
新课进行时
l
y
x
o
解:如图建立直角坐标系.根据题意可设该拱桥形成的抛物线的解析式为y=ax2+2.
∵该抛物线过(2,0),
∴0=4a+2,a=
∵水面下降1m,即当y=-1时,
∴水面宽度增加了
米.
新课进行时
有一座抛物线形拱桥,正常水位时桥下水面宽度为
20m,拱顶距离水面
4m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20
m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
练一练
新课进行时
核心知识点四
利润最大问题
某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价为每件40元,则每星期销售额是
元,销售利润
元.
探究交流
18000
6000
数量关系
(1)销售额=
售价×销售量;
(2)利润=
销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
新课进行时
例3
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售
①每件涨价x元,则每星期售出商品的利润y元,填空:
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
新课进行时
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x
≥0,且x
≥0,因此自变量的取值范围是0
≤x
≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当
时,y=-10×52+100×5+6000=6250.
即定价65元时,最大利润是6250元.
新课进行时
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
降价销售
20
300
20-x
300+18x
y=(20-x)(300+18x)
建立函数关系式:y=(20-x)(300+18x),
即:y=-18x2+60x+6000.
例3
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
6000
新课进行时
综合可知,应定价65元时,才能使利润最大。
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x
≥0,且x
≥0,因此自变量的取值范围是0
≤x
≤20.
③涨价多少元时,利润最大,是多少?
当
时,
即定价57.5元时,最大利润是6050元.
即:y=-18x2+60x+6000,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?
新课进行时
知识要点
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
新课进行时
y=(160+10x)(120-6x)
例4
某旅馆有客房120间,每间房的日租金为160元,每天都客满.经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?
解:设每间客房的日租金提高10x元,则每天客房出租数会减少6x间,则
当x=2时,y有最大值,且y最大=19440.
答:每间客房的日租金提高到180元时,客房日租金的总收入最高,最大收入为19440.
=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
这时每间客房的日租金为160+10×2=180(元).
知识小结
4
知识小结
商品利润最大问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降件:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
随堂演练
5
随堂演练
1.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20
≤x
≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为
元.
25
2.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为
.
每月利润w(元)与衬衣售价x(元)之间的函数关系式为
.(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
随堂演练
3.足球被从地面上踢起,它距地面的高度h(m)可用公式h=
-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
4.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为
,那么铅球运动过程中最高点离地面的距离为
米.
x
y
O
2
随堂演练
5.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
C
随堂演练
6.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
x
y
5
16
O
7
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.即销售单价定为10元时,销售利润最大,25元;
(2)由对称性知y=16时,x=7和13.
故销售单价在7
≤x
≤13时,利润不低于16元.
课后作业
6
文本
文本
文本
单击此处添加文本
文本
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第二十六章
二次函数
26.3
实践与探索
第1课时
运用二次函数解决实际问题
华东师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.(重点)
2.利用二次函数解决拱桥及运动中的有关问题.
(重、难点)
3.能运用二次函数的图象与性质进行决策.
情景导学
2
情景导学
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
新课进行时
3
新课进行时
核心知识点一
利用二次函数解决实物抛物线形问题
建立函数模型
这是什么样的函数呢?
拱桥的纵截面是抛物线,所以应当是个二次函数。
你能想出办法来吗?
合作探究
新课进行时
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图。
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0.0),因此这个二次函数的形式为
新课进行时
x
O
y
-2
-4
2
1
-2
-1
A
如何确定a是多少?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
因此,
,其中
|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
解得
新课进行时
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时
从而
因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
新课进行时
知识要点
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的图象和性质求解
实际问题的解
新课进行时
例1
某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
典例精析
新课进行时
解:建立如图所示的坐标系,
根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
数学化
●B(1,2.25)
(0,1.25)
●
C
●
D
o
A
x
y
新课进行时
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0)
;同理,点
D的坐标为(-2.5,0)
.
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=-
(x-1)2+2.25.
●B(1,2.25)
(0,1.25)
●
D
o
A
x
y
●
C
新课进行时
核心知识点二
利用二次函数解决运动中抛物线型问题
例2:如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
新课进行时
解:如图,建立直角坐标系.
则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).
以点C表示运动员投篮球的出手处.
x
y
O
新课进行时
解得
a=-0.2,
k=3.5,
设以y轴为对称轴的抛物线的解析式为
y=a(x-0)2+k
,
即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=-0.2x2+3.5.
当
x=-2.5时,y=2.25
.
故该运动员出手时的高度为2.25m.
2.25a+k=3.05,
k=3.5,
x
y
O
新课进行时
核心知识点三
拱桥问题
问题1
图中是抛物线形拱桥,当拱顶离水面
2m时,水面宽
4m
.
水面下降
1m,水面宽度增加多少?
互动探究
新课进行时
(1)求宽度增加多少需要什么数据?
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
想一想
新课进行时
问题2
如何建立直角坐标系?
l
问题3
解决本题的关键是什么?
y
x
o
解:如图建立直角坐标系.
解:建立合适的直角坐标系.
新课进行时
l
y
x
o
解:如图建立直角坐标系.根据题意可设该拱桥形成的抛物线的解析式为y=ax2+2.
∵该抛物线过(2,0),
∴0=4a+2,a=
∵水面下降1m,即当y=-1时,
∴水面宽度增加了
米.
新课进行时
有一座抛物线形拱桥,正常水位时桥下水面宽度为
20m,拱顶距离水面
4m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20
m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
练一练
新课进行时
核心知识点四
利润最大问题
某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价为每件40元,则每星期销售额是
元,销售利润
元.
探究交流
18000
6000
数量关系
(1)销售额=
售价×销售量;
(2)利润=
销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
新课进行时
例3
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售
①每件涨价x元,则每星期售出商品的利润y元,填空:
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
新课进行时
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x
≥0,且x
≥0,因此自变量的取值范围是0
≤x
≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当
时,y=-10×52+100×5+6000=6250.
即定价65元时,最大利润是6250元.
新课进行时
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
降价销售
20
300
20-x
300+18x
y=(20-x)(300+18x)
建立函数关系式:y=(20-x)(300+18x),
即:y=-18x2+60x+6000.
例3
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
6000
新课进行时
综合可知,应定价65元时,才能使利润最大。
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x
≥0,且x
≥0,因此自变量的取值范围是0
≤x
≤20.
③涨价多少元时,利润最大,是多少?
当
时,
即定价57.5元时,最大利润是6050元.
即:y=-18x2+60x+6000,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?
新课进行时
知识要点
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
新课进行时
y=(160+10x)(120-6x)
例4
某旅馆有客房120间,每间房的日租金为160元,每天都客满.经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?
解:设每间客房的日租金提高10x元,则每天客房出租数会减少6x间,则
当x=2时,y有最大值,且y最大=19440.
答:每间客房的日租金提高到180元时,客房日租金的总收入最高,最大收入为19440.
=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
这时每间客房的日租金为160+10×2=180(元).
知识小结
4
知识小结
商品利润最大问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降件:要保证单件利润≥0.
确定最大利润
利用配方法或公式求最大值或利用函数简图和性质求出.
随堂演练
5
随堂演练
1.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20
≤x
≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为
元.
25
2.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为
.
每月利润w(元)与衬衣售价x(元)之间的函数关系式为
.(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
随堂演练
3.足球被从地面上踢起,它距地面的高度h(m)可用公式h=
-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
4.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为
,那么铅球运动过程中最高点离地面的距离为
米.
x
y
O
2
随堂演练
5.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
C
随堂演练
6.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
x
y
5
16
O
7
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.即销售单价定为10元时,销售利润最大,25元;
(2)由对称性知y=16时,x=7和13.
故销售单价在7
≤x
≤13时,利润不低于16元.
课后作业
6
文本
文本
文本
单击此处添加文本
文本
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
