26.3 实践与探索 课件(共23张PPT)
文档属性
| 名称 | 26.3 实践与探索 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 15:34:34 | ||
图片预览




文档简介
(共22张PPT)
第二十六章 二次函数
26.3 实践与探索
华东师大版 九年级数学下册 教学课件
情景导学
1
情景导学
二次函数解析式的几种表达式
1.一般式:
2.顶点式:
3.交点式:
其中,抛物线与x轴的两个交点坐标为
新课进行时
2
新课进行时
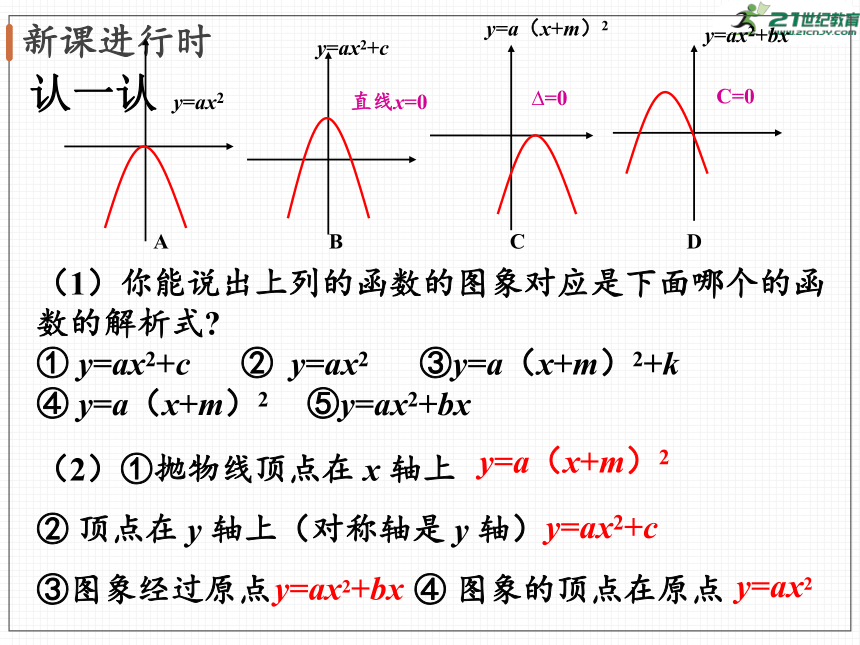
认一认
(1)你能说出上列的函数的图象对应是下面哪个的函数的解析式
① y=ax2+c ② y=ax2 ③y=a(x+m)2+k
④ y=a(x+m)2 ⑤y=ax2+bx
A B C D
(2)①抛物线顶点在 x 轴上
② 顶点在 y 轴上(对称轴是 y 轴)
③图象经过原点 ④ 图象的顶点在原点
=0
C=0
直线x=0
y=ax2+c
y=a(x+m)2
y=ax2+bx
y=ax2
y=a(x+m)2
y=ax2+c
y=ax2+bx
y=ax2
新课进行时
用数学的眼睛观察世界
新课进行时
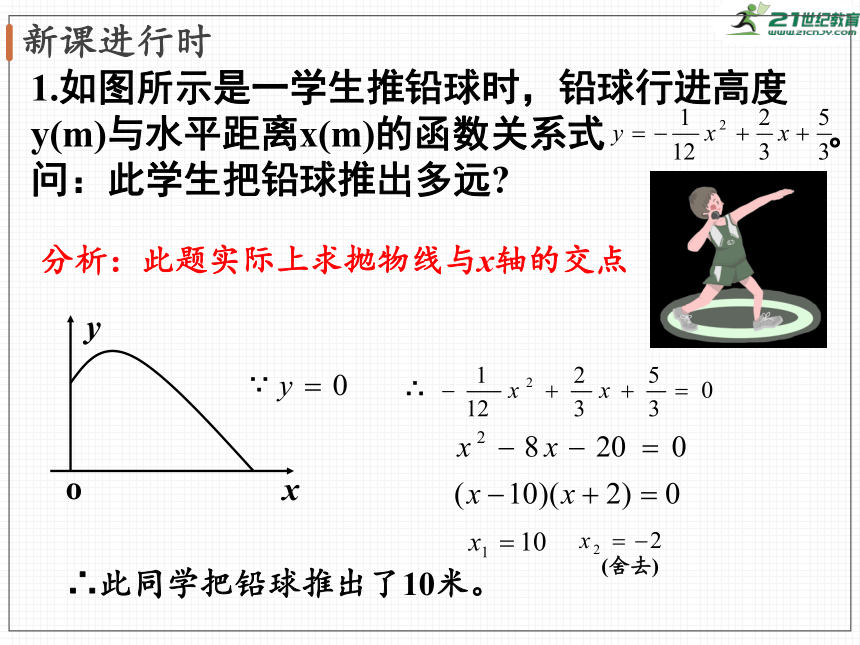
1.如图所示是一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数关系式 。
问:此学生把铅球推出多远
o
y
x
分析:此题实际上求抛物线与x轴的交点
∴此同学把铅球推出了10米。
∵
∴
(舍去)
新课进行时
2.一个涵洞截面成抛物线形,如图26.3.2.现测得,当水面宽AB=1.6 m时,涵洞顶点与水面的距离为OC=2.4 m.这时,离开水面1.5 m处,涵洞宽ED是多少 是否会超过1 m
由图象知,点B(0.8,-2.4)在抛物线上,
解:如图建立平面直角坐标系,
设涵洞所成的抛物线的解析式为:
(-0.8,-2.4)
(0.8,-2.4)
∴ 0.82a= - 2.4,
解得:
∴ 抛物线的解析式为:
当y=-(2.4-1.5)=-0.9时,
∴DE=
<1m
≈0.98(m)
答:离开水面1.5 m处,涵洞宽ED约是0.98m,不会超过1 m。
新课进行时
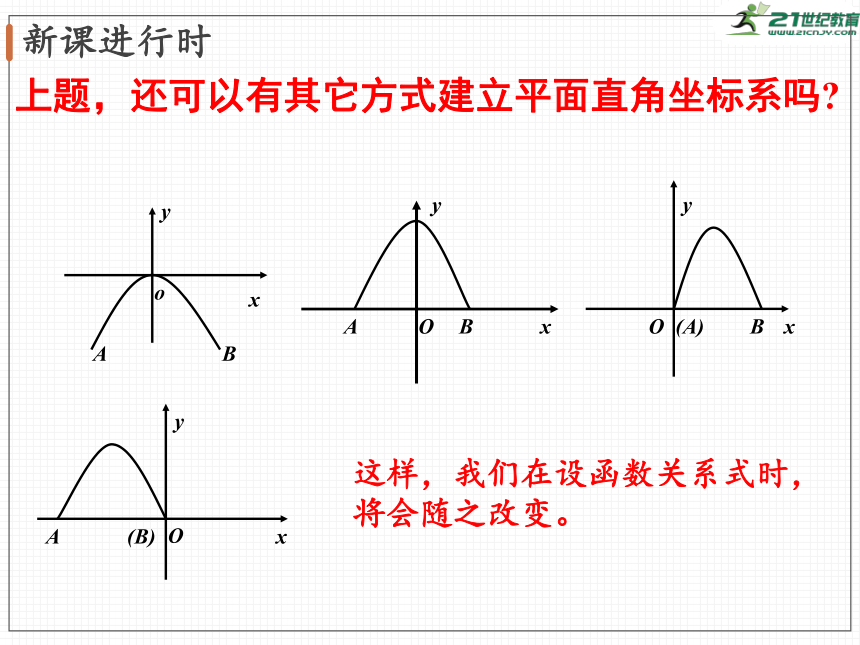
上题,还可以有其它方式建立平面直角坐标系吗
A
y
B
x
O
(A)
B
x
O
y
(B)
A
y
O
x
这样,我们在设函数关系式时,将会随之改变。
A
B
o
y
x
新课进行时
c
3.如图,一名运动员在距离篮下4米处跳起投篮,篮球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最高度3.5米,然后准确落入篮筐.已知篮筐中心到地面距离为3.05米.
(1)求篮球运行路线的抛物线的函数关系式。
(2)如果他的身高为1.9米,在这次跳投中,球在头顶上方0.15米处出手,问求出手时,他跳离地面的高度是多少
x
y
(0,3.5)
(1.5,3.05)
解:(1)建立如图所示的直角坐标系,则,顶点A(0, 3.5),B(1.5,3.05)
y=ax +3.5
设所求的抛物线为:
∵ 抛物线经过点B(1.5,3.05),
∴ 3.05=1.52a+3.5
a=–0.2
∴抛物线的解析式为:y=–0.2x +3.5
(2)
(-2.5, )
当x=–2.5时,
=2.25
y=
-0.2×(-2.5)2+3.5
∴他跳离地面的高度为:
2.25-1.9-0.15=
0.2m
新课进行时
咱来试一试
你知道吗 平时我们在跳大绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m
2.5m
4m
1m
甲
乙
丙
丁
x
y
o
(0,1)
(4,1)
(1,1.5)
知识小结
3
知识小结
利用二次函数的性质解决应用题的一般步骤:
1.设定实际问题中的变量;
2.建立变量与变量之间的函数关系式;
3.确定自变量的取值范围,保证自变量具有实际意义。
随堂演练
4
随堂演练
1.如图,拱桥是抛物线形,其函数解析式为
,当水位线在AB位置时,水面宽为12m,这时水面离桥顶的高度h是 ( )
A.3m B. m C. m D.9m
D
随堂演练
2.某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水呈抛物线状(抛物线所在平面与墙面垂直),如图所示,如果抛物线的最高点M离墙l米,离地面 米,则水流落地点B离墙的距离OB是 ( )
A.2米 B.3米 C.4米 D.5米
B
x
y
(0,10)
随堂演练
3.某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子OA,柱高为1.25 m.水流在各个方向上沿形状相同的抛物线路径落下,要求设计成水流在离OA距离为1 m处达到距水面最大高度2.25m。如图(1)所示.
请回答下列问题:
(1)如果不计其他因素,那么水池的半径至少为多少时才能使喷出的水流都落在水池内
(2)若水流喷出的抛物线形状与(1)相同,水池半径为3.5m,只要使水流不落到池外,此时水流的最大高度约为多少米 (精确到0.1m)
1
2.25
(0,1.25)
c
(1,2.25)
随堂演练
1
2.25
(0,1.25)
c
(1,2.25)
A(0,1.25),C(1,2.25)
设抛物线的解析式为:
将A(0,1.25)代入上式得:
解之得:
∴抛物线的解析式为:
当y=0时,
∴
∴
(舍去)
答:至少2.5m
解:(1)以O为原点,OA为y轴建立
平面直角坐标系,则
随堂演练
∴水流最大高度可达3.7m。
(0,1.25)
(2) ∵抛物线的形状与(1)相同,
(3.5,0)
∴设抛物线的解析式为:
∵抛物线过A(0,1.25),B(3.5,0)
∴代入解析式得:
解之得:
∴抛物线的解析式为:
课后作业
5
文本
文本
文本
单击此处添加文本
文本
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK YOU FOR LISTENING
第二十六章 二次函数
26.3 实践与探索
华东师大版 九年级数学下册 教学课件
情景导学
1
情景导学
二次函数解析式的几种表达式
1.一般式:
2.顶点式:
3.交点式:
其中,抛物线与x轴的两个交点坐标为
新课进行时
2
新课进行时
认一认
(1)你能说出上列的函数的图象对应是下面哪个的函数的解析式
① y=ax2+c ② y=ax2 ③y=a(x+m)2+k
④ y=a(x+m)2 ⑤y=ax2+bx
A B C D
(2)①抛物线顶点在 x 轴上
② 顶点在 y 轴上(对称轴是 y 轴)
③图象经过原点 ④ 图象的顶点在原点
=0
C=0
直线x=0
y=ax2+c
y=a(x+m)2
y=ax2+bx
y=ax2
y=a(x+m)2
y=ax2+c
y=ax2+bx
y=ax2
新课进行时
用数学的眼睛观察世界
新课进行时
1.如图所示是一学生推铅球时,铅球行进高度y(m)与水平距离x(m)的函数关系式 。
问:此学生把铅球推出多远
o
y
x
分析:此题实际上求抛物线与x轴的交点
∴此同学把铅球推出了10米。
∵
∴
(舍去)
新课进行时
2.一个涵洞截面成抛物线形,如图26.3.2.现测得,当水面宽AB=1.6 m时,涵洞顶点与水面的距离为OC=2.4 m.这时,离开水面1.5 m处,涵洞宽ED是多少 是否会超过1 m
由图象知,点B(0.8,-2.4)在抛物线上,
解:如图建立平面直角坐标系,
设涵洞所成的抛物线的解析式为:
(-0.8,-2.4)
(0.8,-2.4)
∴ 0.82a= - 2.4,
解得:
∴ 抛物线的解析式为:
当y=-(2.4-1.5)=-0.9时,
∴DE=
<1m
≈0.98(m)
答:离开水面1.5 m处,涵洞宽ED约是0.98m,不会超过1 m。
新课进行时
上题,还可以有其它方式建立平面直角坐标系吗
A
y
B
x
O
(A)
B
x
O
y
(B)
A
y
O
x
这样,我们在设函数关系式时,将会随之改变。
A
B
o
y
x
新课进行时
c
3.如图,一名运动员在距离篮下4米处跳起投篮,篮球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最高度3.5米,然后准确落入篮筐.已知篮筐中心到地面距离为3.05米.
(1)求篮球运行路线的抛物线的函数关系式。
(2)如果他的身高为1.9米,在这次跳投中,球在头顶上方0.15米处出手,问求出手时,他跳离地面的高度是多少
x
y
(0,3.5)
(1.5,3.05)
解:(1)建立如图所示的直角坐标系,则,顶点A(0, 3.5),B(1.5,3.05)
y=ax +3.5
设所求的抛物线为:
∵ 抛物线经过点B(1.5,3.05),
∴ 3.05=1.52a+3.5
a=–0.2
∴抛物线的解析式为:y=–0.2x +3.5
(2)
(-2.5, )
当x=–2.5时,
=2.25
y=
-0.2×(-2.5)2+3.5
∴他跳离地面的高度为:
2.25-1.9-0.15=
0.2m
新课进行时
咱来试一试
你知道吗 平时我们在跳大绳时,绳甩到最高处的形状可近似的看为抛物线,如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处时,刚好通过他们的头顶,已知学生丙的身高是1.5米,请你算一算学生丁的身高。
1m
2.5m
4m
1m
甲
乙
丙
丁
x
y
o
(0,1)
(4,1)
(1,1.5)
知识小结
3
知识小结
利用二次函数的性质解决应用题的一般步骤:
1.设定实际问题中的变量;
2.建立变量与变量之间的函数关系式;
3.确定自变量的取值范围,保证自变量具有实际意义。
随堂演练
4
随堂演练
1.如图,拱桥是抛物线形,其函数解析式为
,当水位线在AB位置时,水面宽为12m,这时水面离桥顶的高度h是 ( )
A.3m B. m C. m D.9m
D
随堂演练
2.某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水呈抛物线状(抛物线所在平面与墙面垂直),如图所示,如果抛物线的最高点M离墙l米,离地面 米,则水流落地点B离墙的距离OB是 ( )
A.2米 B.3米 C.4米 D.5米
B
x
y
(0,10)
随堂演练
3.某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子OA,柱高为1.25 m.水流在各个方向上沿形状相同的抛物线路径落下,要求设计成水流在离OA距离为1 m处达到距水面最大高度2.25m。如图(1)所示.
请回答下列问题:
(1)如果不计其他因素,那么水池的半径至少为多少时才能使喷出的水流都落在水池内
(2)若水流喷出的抛物线形状与(1)相同,水池半径为3.5m,只要使水流不落到池外,此时水流的最大高度约为多少米 (精确到0.1m)
1
2.25
(0,1.25)
c
(1,2.25)
随堂演练
1
2.25
(0,1.25)
c
(1,2.25)
A(0,1.25),C(1,2.25)
设抛物线的解析式为:
将A(0,1.25)代入上式得:
解之得:
∴抛物线的解析式为:
当y=0时,
∴
∴
(舍去)
答:至少2.5m
解:(1)以O为原点,OA为y轴建立
平面直角坐标系,则
随堂演练
∴水流最大高度可达3.7m。
(0,1.25)
(2) ∵抛物线的形状与(1)相同,
(3.5,0)
∴设抛物线的解析式为:
∵抛物线过A(0,1.25),B(3.5,0)
∴代入解析式得:
解之得:
∴抛物线的解析式为:
课后作业
5
文本
文本
文本
单击此处添加文本
文本
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK YOU FOR LISTENING
