第26章 小结与复习 课件(共31张PPT)
文档属性
| 名称 | 第26章 小结与复习 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 13:36:57 | ||
图片预览








文档简介
(共31张PPT)
第二十六章
二次函数
小结与复习
华东师大版
九年级数学下册
教学课件
要点梳理
1
要点梳理
1.二次函数的概念
一般地,形如
(a,b,c是常数,
)的函数,叫做二次函数.
y=ax2+bx+c
a
≠0
[注意]
(1)等号右边必须是整式;(2)自变量的最高次数是2;(3)当b=0,c=0时,y=ax2是特殊的二次函数.
2.二次函数的图象
二次函数的图象是一条
,它是
对称图形,其对称轴平行于_____轴.
[注意]
二次函数y=ax2+bx+c的图象的形状、大小、开口方向只与a有关.
抛物线
轴
y
要点梳理
(1)一般式:____________________;
3.二次函数的解析式
y=ax2+bx+c(a≠0)
(2)顶点式:____________________;
y=a(x-h)2+k
(a≠0)
(3)交点式:____________________;
y=a(x-x1)(x-x2)
(a≠0)
4.二次函数的平移
一般地,平移二次函数y=ax2的图象可得到二次函数y=a(x-h)2+k的图象.
y=ax2
上、下平移
y=ax2
左、右平移
左、右平移
上、下平移
上、下移且左、右移
[注意]
抓住顶点坐标的变化,熟记平移规律:左加右减,上加下减.
要点梳理
二次函数
y=a(x-h)2+k
y=ax2+bx+c
开口
方向
对称轴
顶点坐标
最值
a>0
a<0
增减性
a>0
a<0
5.二次函数的y=ax2+bx+c的图象与性质:
a>0
开口向上
a
<
0
开口向下
x=h
(h
,
k)
y最小=k
y最大=k
在对称轴左边,
x
↗y↘
;在对称轴右边,
x
↗
y
↗
在对称轴左边,
x
↗y
↗
;在对称轴右边,
x
↗
y
↘
y最小=
y最大=
要点梳理
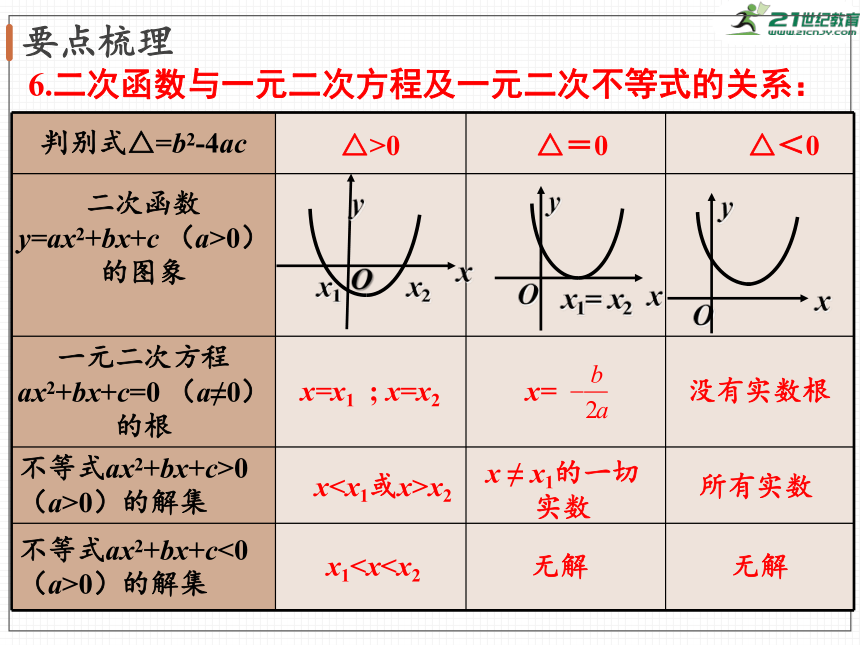
6.二次函数与一元二次方程及一元二次不等式的关系:
判别式△=b2-4ac
二次函数y=ax2+bx+c
(a>0)
的图象
一元二次方程ax2+bx+c=0
(a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
O
x
y
O
x1=
x2
x
y
x
O
y
△>0
△=0
△<0
x=x1
;
x=x2
没有实数根
xx2
x
≠
x1的一切实数
所有实数
x1无解
无解
x=
考点讲练
2
考点讲练
核心知识点一
求抛物线的顶点、对称轴、最值
例1
抛物线y=x2-2x+3的顶点坐标为____.
【解析】
方法一:
配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二:
代入公式
,
,
则顶点坐标为(1,2).
考点讲练
解决此类题目可以先把二次函数y=ax2+bx+c配方为顶点式y=a(x-h)2+k的形式,得到:对称轴是直线x=h,最值为y=k,顶点坐标为(h,k);也可以直接利用公式求解.
方法总结
考点讲练
针对训练
1.对于y=2(x-3)2+2的图象下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
C
考点讲练
核心知识点二
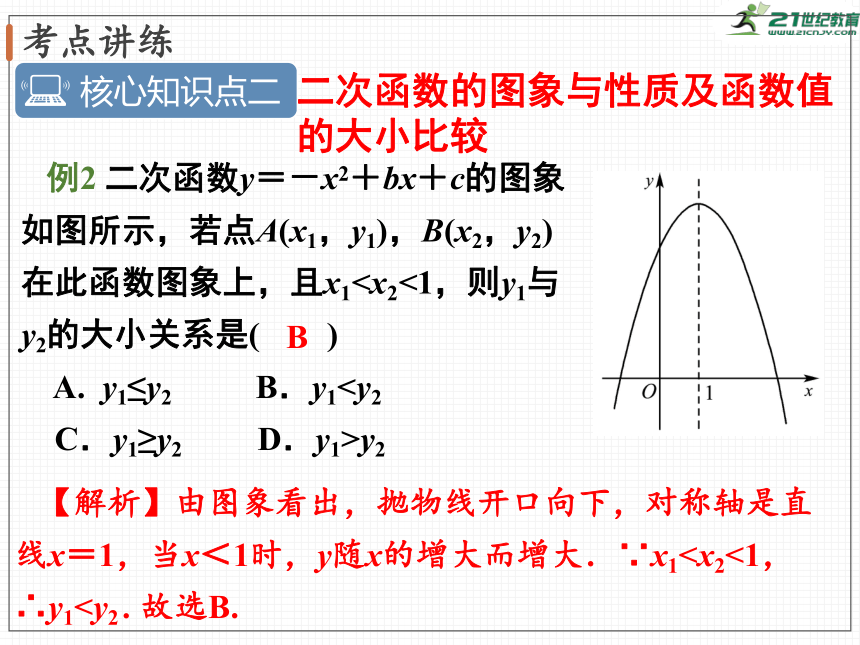
二次函数的图象与性质及函数值的大小比较
例2
二次函数y=-x2+bx+c的图象如图所示,若点A(x1,y1),B(x2,y2)在此函数图象上,且x1A.
y1≤y2
B.y1C.y1≥y2
D.y1>y2
【解析】由图象看出,抛物线开口向下,对称轴是直线x=1,当x<1时,y随x的增大而增大.∵x1.
故选B.
B
考点讲练
当二次函数的表达式与已知点的坐标中含有未知字母时,可以用如下方法比较函数值的大小:
(1)用含有未知字母的代数式表示各函数值,然后进行比较;
(2)在相应的范围内取未知字母的特殊值,采用特殊值法求解;
(3)根据二次函数的性质,结合函数图象比较.
方法总结
考点讲练
针对训练
2.下列函数中,当x>0时,y值随x值增大而减小的是(
)
A.
y=x2
B.y=x-1
C.
D.y=-3x2
D
考点讲练
核心知识点三
二次函数
y=ax2+bx+c(a≠0)的图象与系数a,b,c的关系
例3
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2.
其中正确的个数是( )
A.1 B.2
C.3 D.4
D
考点讲练
【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得
c>0,则abc>0,故①正确;由对称轴x>-1可得2a-b<0,故②正确;由图象上横坐标为
x=-2的点在第三象限可得4a-2b+c<0,故③正确;
由图象上横坐标为x=1的点在第四象限得出a+b+c<0,由图象上横坐标为x=-1的点在第二象限得出
a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.故选D.
【答案】
D
考点讲练
方法总结
1.可根据对称轴的位置确定b的符号:b=0?对称轴是y轴;a、b同号?对称轴在y轴左侧;a、b异号?对称轴在y轴右侧.这个规律可简记为“左同右异”.
2.当x=1时,函数y=a+b+c.当图象上横坐标
x=1的点在x轴上方时,a+b+c>0;当图象上横坐标x=1的点在x轴上时,a+b+c=0;当图象上横坐标x=1的点在x轴下方时,a+b+c<0.同理,可由图象上横坐标x=-1的点判断a-b+c的符号.
考点讲练
针对训练
3.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是(
)
A.b≥-1
B.b≤-1
C.b≥1
D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴
,即b≤1,故选择D
.
D
考点讲练
核心知识点四
抛物线的几何变换
抛物线平移的规律可总结如下口诀:左加右减自变量,上加下减常数项.
例4
将抛物线y=x2-6x+5向上平移
2个单位长度,再向右平移1个单位长度后,得到的抛物线表达式是
( )
A.y=(x-4)2-6
B.y=(x-4)2-2
C.y=(x-2)2-2
D.y=(x-1)2-3
【解析】因为y=x2-6x+5=(x-3)2-4,所以向上平移2个单位长度,再向右平移1个单位长度后,得到的表达式为y=(x-3-1)2-4+2,即y=
(x-4)2-2.故选B.
方法总结
B
考点讲练
针对训练
4.若抛物线
y=-7(x+4)2-1平移得到
y=-7x2,则必须(
)
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向下平移4个单位
B
考点讲练
核心知识点五
二次函数表达式的确定
例5:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的表达式.
待定系数法
解:设所求的二次函数为y=ax2+bx+c,
由题意得:
解得,
a=2,b=-3,c=5.
∴
所求的二次函数表达式为y=2x2-3x+5.
考点讲练
1.若已知图象上的任意三个点,则设一般式求表达式;
2.若已知抛物线的顶点坐标或对称轴与最值时,则可设顶点式求表达式,最后化为一般式;
3.若已知二次函数图象与x轴的交点坐标为
(x1,0)、(x2,0)时,可设交点式求表达式,最后化为一般式.
方法总结
考点讲练
针对训练
5.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的表达式.
解:∵抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同?
a=1或-1.
又∵顶点在直线x=1上,且顶点到x轴的距离为5,
∴顶点为(1,5)或(1,-5).
所以其解析式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
考点讲练
核心知识点六
二次函数与一元二次方程
例6
若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6
B.x1=1,x2=7
C.x1=1,x2=﹣7
D.x1=﹣1,x2=7
【解答】∵二次函数y=x2+mx的对称轴是x=3,
∴-
=3,解得m=-6,
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0,解得x1=-1,x2=7.
故选D.
D
考点讲练
核心知识点七
二次函数的应用
例7
某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)设矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0<x<6.
(2)S=-x2+6x=-(x-3)2+9;
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元).
考点讲练
利用二次函数的知识常解决以下几类问题:最大利润问题,求几何图形面积的最值问题,拱桥问题,运动型几何问题,方案设计问题等.
方法总结
课堂小结
3
知识小结
二次函数
图象画法
抛物线
开口方向
抛物线的顶点坐标和对称轴
二次函数的性质
抛物线的平移
最值
确定
解析式
应用
课后作业
4
文本
文本
文本
单击此处添加文本
文本
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第二十六章
二次函数
小结与复习
华东师大版
九年级数学下册
教学课件
要点梳理
1
要点梳理
1.二次函数的概念
一般地,形如
(a,b,c是常数,
)的函数,叫做二次函数.
y=ax2+bx+c
a
≠0
[注意]
(1)等号右边必须是整式;(2)自变量的最高次数是2;(3)当b=0,c=0时,y=ax2是特殊的二次函数.
2.二次函数的图象
二次函数的图象是一条
,它是
对称图形,其对称轴平行于_____轴.
[注意]
二次函数y=ax2+bx+c的图象的形状、大小、开口方向只与a有关.
抛物线
轴
y
要点梳理
(1)一般式:____________________;
3.二次函数的解析式
y=ax2+bx+c(a≠0)
(2)顶点式:____________________;
y=a(x-h)2+k
(a≠0)
(3)交点式:____________________;
y=a(x-x1)(x-x2)
(a≠0)
4.二次函数的平移
一般地,平移二次函数y=ax2的图象可得到二次函数y=a(x-h)2+k的图象.
y=ax2
上、下平移
y=ax2
左、右平移
左、右平移
上、下平移
上、下移且左、右移
[注意]
抓住顶点坐标的变化,熟记平移规律:左加右减,上加下减.
要点梳理
二次函数
y=a(x-h)2+k
y=ax2+bx+c
开口
方向
对称轴
顶点坐标
最值
a>0
a<0
增减性
a>0
a<0
5.二次函数的y=ax2+bx+c的图象与性质:
a>0
开口向上
a
<
0
开口向下
x=h
(h
,
k)
y最小=k
y最大=k
在对称轴左边,
x
↗y↘
;在对称轴右边,
x
↗
y
↗
在对称轴左边,
x
↗y
↗
;在对称轴右边,
x
↗
y
↘
y最小=
y最大=
要点梳理
6.二次函数与一元二次方程及一元二次不等式的关系:
判别式△=b2-4ac
二次函数y=ax2+bx+c
(a>0)
的图象
一元二次方程ax2+bx+c=0
(a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
O
x
y
O
x1=
x2
x
y
x
O
y
△>0
△=0
△<0
x=x1
;
x=x2
没有实数根
x
x
≠
x1的一切实数
所有实数
x1
无解
x=
考点讲练
2
考点讲练
核心知识点一
求抛物线的顶点、对称轴、最值
例1
抛物线y=x2-2x+3的顶点坐标为____.
【解析】
方法一:
配方,得y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
方法二:
代入公式
,
,
则顶点坐标为(1,2).
考点讲练
解决此类题目可以先把二次函数y=ax2+bx+c配方为顶点式y=a(x-h)2+k的形式,得到:对称轴是直线x=h,最值为y=k,顶点坐标为(h,k);也可以直接利用公式求解.
方法总结
考点讲练
针对训练
1.对于y=2(x-3)2+2的图象下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为y=3
C.当x≥3时,y随x的增大而增大
D.当x≥3时,y随x的增大而减小
C
考点讲练
核心知识点二
二次函数的图象与性质及函数值的大小比较
例2
二次函数y=-x2+bx+c的图象如图所示,若点A(x1,y1),B(x2,y2)在此函数图象上,且x1
y1≤y2
B.y1
D.y1>y2
【解析】由图象看出,抛物线开口向下,对称轴是直线x=1,当x<1时,y随x的增大而增大.∵x1
故选B.
B
考点讲练
当二次函数的表达式与已知点的坐标中含有未知字母时,可以用如下方法比较函数值的大小:
(1)用含有未知字母的代数式表示各函数值,然后进行比较;
(2)在相应的范围内取未知字母的特殊值,采用特殊值法求解;
(3)根据二次函数的性质,结合函数图象比较.
方法总结
考点讲练
针对训练
2.下列函数中,当x>0时,y值随x值增大而减小的是(
)
A.
y=x2
B.y=x-1
C.
D.y=-3x2
D
考点讲练
核心知识点三
二次函数
y=ax2+bx+c(a≠0)的图象与系数a,b,c的关系
例3
已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc>0;②2a-b<0;③4a-2b+c<0;④(a+c)2<b2.
其中正确的个数是( )
A.1 B.2
C.3 D.4
D
考点讲练
【解析】由图象开口向下可得a<0,由对称轴在y轴左侧可得b<0,由图象与y轴交于正半轴可得
c>0,则abc>0,故①正确;由对称轴x>-1可得2a-b<0,故②正确;由图象上横坐标为
x=-2的点在第三象限可得4a-2b+c<0,故③正确;
由图象上横坐标为x=1的点在第四象限得出a+b+c<0,由图象上横坐标为x=-1的点在第二象限得出
a-b+c>0,则(a+b+c)(a-b+c)<0,即(a+c)2-b2<0,可得(a+c)2<b2,故④正确.故选D.
【答案】
D
考点讲练
方法总结
1.可根据对称轴的位置确定b的符号:b=0?对称轴是y轴;a、b同号?对称轴在y轴左侧;a、b异号?对称轴在y轴右侧.这个规律可简记为“左同右异”.
2.当x=1时,函数y=a+b+c.当图象上横坐标
x=1的点在x轴上方时,a+b+c>0;当图象上横坐标x=1的点在x轴上时,a+b+c=0;当图象上横坐标x=1的点在x轴下方时,a+b+c<0.同理,可由图象上横坐标x=-1的点判断a-b+c的符号.
考点讲练
针对训练
3.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是(
)
A.b≥-1
B.b≤-1
C.b≥1
D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴
,即b≤1,故选择D
.
D
考点讲练
核心知识点四
抛物线的几何变换
抛物线平移的规律可总结如下口诀:左加右减自变量,上加下减常数项.
例4
将抛物线y=x2-6x+5向上平移
2个单位长度,再向右平移1个单位长度后,得到的抛物线表达式是
( )
A.y=(x-4)2-6
B.y=(x-4)2-2
C.y=(x-2)2-2
D.y=(x-1)2-3
【解析】因为y=x2-6x+5=(x-3)2-4,所以向上平移2个单位长度,再向右平移1个单位长度后,得到的表达式为y=(x-3-1)2-4+2,即y=
(x-4)2-2.故选B.
方法总结
B
考点讲练
针对训练
4.若抛物线
y=-7(x+4)2-1平移得到
y=-7x2,则必须(
)
A.先向左平移4个单位,再向下平移1个单位
B.先向右平移4个单位,再向上平移1个单位
C.先向左平移1个单位,再向下平移4个单位
D.先向右平移1个单位,再向下平移4个单位
B
考点讲练
核心知识点五
二次函数表达式的确定
例5:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的表达式.
待定系数法
解:设所求的二次函数为y=ax2+bx+c,
由题意得:
解得,
a=2,b=-3,c=5.
∴
所求的二次函数表达式为y=2x2-3x+5.
考点讲练
1.若已知图象上的任意三个点,则设一般式求表达式;
2.若已知抛物线的顶点坐标或对称轴与最值时,则可设顶点式求表达式,最后化为一般式;
3.若已知二次函数图象与x轴的交点坐标为
(x1,0)、(x2,0)时,可设交点式求表达式,最后化为一般式.
方法总结
考点讲练
针对训练
5.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的表达式.
解:∵抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同?
a=1或-1.
又∵顶点在直线x=1上,且顶点到x轴的距离为5,
∴顶点为(1,5)或(1,-5).
所以其解析式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
考点讲练
核心知识点六
二次函数与一元二次方程
例6
若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A.x1=0,x2=6
B.x1=1,x2=7
C.x1=1,x2=﹣7
D.x1=﹣1,x2=7
【解答】∵二次函数y=x2+mx的对称轴是x=3,
∴-
=3,解得m=-6,
∴关于x的方程x2+mx=7可化为x2-6x-7=0,
即(x+1)(x-7)=0,解得x1=-1,x2=7.
故选D.
D
考点讲练
核心知识点七
二次函数的应用
例7
某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)设矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0<x<6.
(2)S=-x2+6x=-(x-3)2+9;
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元).
考点讲练
利用二次函数的知识常解决以下几类问题:最大利润问题,求几何图形面积的最值问题,拱桥问题,运动型几何问题,方案设计问题等.
方法总结
课堂小结
3
知识小结
二次函数
图象画法
抛物线
开口方向
抛物线的顶点坐标和对称轴
二次函数的性质
抛物线的平移
最值
确定
解析式
应用
课后作业
4
文本
文本
文本
单击此处添加文本
文本
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
