安徽合肥市庐阳区四十五中2020-2021学年第一学期九年级期中数学试卷(Word版 含答案)
文档属性
| 名称 | 安徽合肥市庐阳区四十五中2020-2021学年第一学期九年级期中数学试卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 273.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 13:52:11 | ||
图片预览

文档简介
合肥庐阳区四十五中2020-2021第一学期九年级期中数学试卷(含答案)
一、选择题(本大题共10小题,每小题4分,满分
40分)
1、已知,则的值为(
)
A
B
C
D
2、下列函数中,当x>
0时,y随x的增大而减小的是(
)
A
y=-x2
B
y=x-1
C
y=x2-3
D
y=8x
3、将二次函数y=(x-1)2+2的图象向上平移3个单位长度,再向左平移2个单位长度,得到的抛物线相应的函数表达式为(
)
A.
y=(x+2)
2-1
B.
y=(x-3)
2+5
C.
y=(x+1)
2+5
D.
y=(x-1)
2+5
4、如图,AB//CD//EF,AD=4,BC=DF=3,则BE的长为(
)
A
B
C
4
D
6
第4题图
第8题图
第9题图
5、已知:在△ABC中,∠A=78°,AB=4,AC=6,下列阴影部分的三角形与原△ABC不相似的是(
)
A
B
C
D
6、函数y=ax2-a与y=ax-a(a≠0)在同一坐标系中的图象可能是(
)
A
B
C
D
7、点B是线段AC的黄金分割点,且AB<
BC,若AC=2,则BC的长为(
)
A
B
C
D
8、如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=且经过点(2,0),下列说法:①abc<
0;
②a+b=0;
③4a+2b+c<
0;④若(-,y1)、(,y2)是抛物线上的两点,则y1<
y2;⑤b>
m(am+b)
(其中
m≠)。其中说法正确的是(
)
A.
①②④⑤
B.
①②④
C
①④⑤
D.
③④⑤
9、如图,直线11//l2//l3,一等腰Rt△ABC的三个顶点A、B、C分别在直线11、l2、l3上,∠ACCB=90°,AC交l2于点D,若11与l2的距离为1,11与l3的距离为4,则AD长是(
)
A
B
C
D
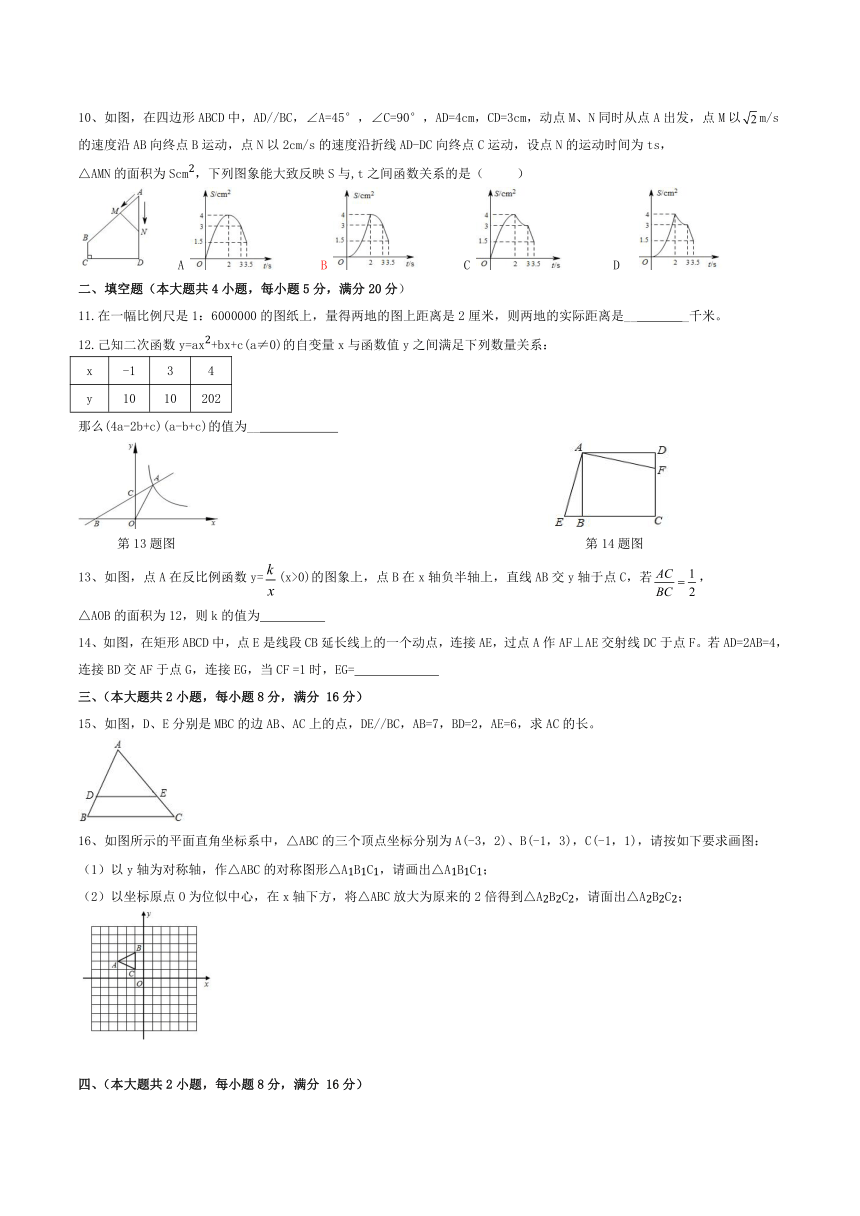
10、如图,在四边形ABCD中,AD//BC,∠A=45°,∠C=90°,AD=4cm,CD=3cm,动点M、N同时从点A出发,点M以m/s的速度沿AB向终点B运动,点N以2cm/s的速度沿折线AD-DC向终点C运动,设点N的运动时间为ts,
△AMN的面积为Scm2,下列图象能大致反映S与,t之间函数关系的是(
)
A
B
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在一幅比例尺是1:6000000的图纸上,量得两地的图上距离是2厘米,则两地的实际距离是__
_千米。
12.己知二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y之间满足下列数量关系:
x
-1
3
4
y
10
10
202
那么(4a-2b+c)(a-b+c)的值为__
第13题图
第14题图
13、如图,点A在反比例函数y=(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,
△AOB的面积为12,则k的值为
14、如图,在矩形ABCD中,点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F。若AD=2AB=4,连接BD交AF于点G,连接EG,当CF
=1时,EG=
三、(本大题共2小题,每小题8分,满分
16分)
15、如图,D、E分别是MBC的边AB、AC上的点,DE//BC,AB=7,BD=2,AE=6,求AC的长。
16、如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,2)、B(-1,3),C(-1,1),请按如下要求画图:
(1)以y轴为对称轴,作△ABC的对称图形△A1B1C1,请画出△A1B1C1;
(2)以坐标原点O为位似中心,在x轴下方,将△ABC放大为原来的2倍得到△A2B2C2,请面出△A2B2C2;
四、(本大题共2小题,每小题8分,满分
16分)
17、如图,已知抛物线y=x2+bx+c经过A(-1,0)、C(0,-3)两点。
(1)求抛物线的解析式和顶点坐标;
(2)当0<
x<
3时,请直接写出y的取值范围。
18、如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F
(1)求证:△ADF∽△EAB;
(2)若DF=6,求线段EF的长。
五、(本大题共2小题,每小题10分,满分
20分)
19.某公园草坪的防护栏形状是抛物线形,为了牢固起见,每段护栏需婴间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m
(如图),求其中防护栏支柱A1B1的长度。
20、如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F。
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求出△FCD的面积。
六、(本题满分
12分)
21、如图,已知一次函数y=x+b的图象与反比例函数y=(x<0)的图象交于点A(-1,2)
和点B,点P在y轴上。
(1)求b和k的值;
(2)当PA+PB最小时,点P的坐标为____
_;
(3)当x+b<时,请直接写出x的取值范围。
七、(本题满分
12分)
22.某服装批发市场销售种衬衫,村衫每件进货价为50元,规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件)
60
65
70
销售量y(件)
1400
1300
1200
(1)求出y与x之间的函数表达式;(不需
要求自变量x的取值范围)
(2)该批发市场每月想从这种衬杉销售中获利24000元,又想尽量给客户实惠,该如何给这种村衫定价?
(3)物价部门规定,该衬杉的每件利润不允许高于进货价的30%,设这种衬杉每月的总利润为w(元),那么售价定为多少元可获得最大利润?最大利润是多少?
八、(本题满分
14分)
23、如图,△ABC中,AB=AC,AB⊥AC,点D、E分别是BC、AC的中点,AF⊥BE与点F。
(1)求证:AE2=FE·BE;
(2)求∠AFC的大小;
(3)若DF=2,求△ABF的面积;
合肥庐阳区四十五中2020-2021第一学期九年级期中数学试卷答案
1
2
3
4
5
6
7
8
9
10
A
A
B
B
C
D
D
A
B
B
11、
12;
12、
2020;
13、
12;
14、
或;
15、;
16、
17、(1)y=(x-1)2-4;(1,-4);(2)-4≤y<0;
18、
19、
20、
21、(1)b=3;
k=-2;
(2)(0,);
(3)x>-2或-1<x<0;
22、(1)y=-20x+2600;
(2)70;
(3)售价定为65元时,最大利润19500元;
23、(1)∵AF⊥BE,AB⊥AC,∴∠AFE=∠BAE=90°,∠AEF=∠BEA,∴△AEF∽△BEA,∴AE2=FE·BE;
(2)135°;
(3)2;
一、选择题(本大题共10小题,每小题4分,满分
40分)
1、已知,则的值为(
)
A
B
C
D
2、下列函数中,当x>
0时,y随x的增大而减小的是(
)
A
y=-x2
B
y=x-1
C
y=x2-3
D
y=8x
3、将二次函数y=(x-1)2+2的图象向上平移3个单位长度,再向左平移2个单位长度,得到的抛物线相应的函数表达式为(
)
A.
y=(x+2)
2-1
B.
y=(x-3)
2+5
C.
y=(x+1)
2+5
D.
y=(x-1)
2+5
4、如图,AB//CD//EF,AD=4,BC=DF=3,则BE的长为(
)
A
B
C
4
D
6
第4题图
第8题图
第9题图
5、已知:在△ABC中,∠A=78°,AB=4,AC=6,下列阴影部分的三角形与原△ABC不相似的是(
)
A
B
C
D
6、函数y=ax2-a与y=ax-a(a≠0)在同一坐标系中的图象可能是(
)
A
B
C
D
7、点B是线段AC的黄金分割点,且AB<
BC,若AC=2,则BC的长为(
)
A
B
C
D
8、如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=且经过点(2,0),下列说法:①abc<
0;
②a+b=0;
③4a+2b+c<
0;④若(-,y1)、(,y2)是抛物线上的两点,则y1<
y2;⑤b>
m(am+b)
(其中
m≠)。其中说法正确的是(
)
A.
①②④⑤
B.
①②④
C
①④⑤
D.
③④⑤
9、如图,直线11//l2//l3,一等腰Rt△ABC的三个顶点A、B、C分别在直线11、l2、l3上,∠ACCB=90°,AC交l2于点D,若11与l2的距离为1,11与l3的距离为4,则AD长是(
)
A
B
C
D
10、如图,在四边形ABCD中,AD//BC,∠A=45°,∠C=90°,AD=4cm,CD=3cm,动点M、N同时从点A出发,点M以m/s的速度沿AB向终点B运动,点N以2cm/s的速度沿折线AD-DC向终点C运动,设点N的运动时间为ts,
△AMN的面积为Scm2,下列图象能大致反映S与,t之间函数关系的是(
)
A
B
C
D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在一幅比例尺是1:6000000的图纸上,量得两地的图上距离是2厘米,则两地的实际距离是__
_千米。
12.己知二次函数y=ax2+bx+c(a≠0)的自变量x与函数值y之间满足下列数量关系:
x
-1
3
4
y
10
10
202
那么(4a-2b+c)(a-b+c)的值为__
第13题图
第14题图
13、如图,点A在反比例函数y=(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,
△AOB的面积为12,则k的值为
14、如图,在矩形ABCD中,点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F。若AD=2AB=4,连接BD交AF于点G,连接EG,当CF
=1时,EG=
三、(本大题共2小题,每小题8分,满分
16分)
15、如图,D、E分别是MBC的边AB、AC上的点,DE//BC,AB=7,BD=2,AE=6,求AC的长。
16、如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,2)、B(-1,3),C(-1,1),请按如下要求画图:
(1)以y轴为对称轴,作△ABC的对称图形△A1B1C1,请画出△A1B1C1;
(2)以坐标原点O为位似中心,在x轴下方,将△ABC放大为原来的2倍得到△A2B2C2,请面出△A2B2C2;
四、(本大题共2小题,每小题8分,满分
16分)
17、如图,已知抛物线y=x2+bx+c经过A(-1,0)、C(0,-3)两点。
(1)求抛物线的解析式和顶点坐标;
(2)当0<
x<
3时,请直接写出y的取值范围。
18、如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为F
(1)求证:△ADF∽△EAB;
(2)若DF=6,求线段EF的长。
五、(本大题共2小题,每小题10分,满分
20分)
19.某公园草坪的防护栏形状是抛物线形,为了牢固起见,每段护栏需婴间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m
(如图),求其中防护栏支柱A1B1的长度。
20、如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F。
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求出△FCD的面积。
六、(本题满分
12分)
21、如图,已知一次函数y=x+b的图象与反比例函数y=(x<0)的图象交于点A(-1,2)
和点B,点P在y轴上。
(1)求b和k的值;
(2)当PA+PB最小时,点P的坐标为____
_;
(3)当x+b<时,请直接写出x的取值范围。
七、(本题满分
12分)
22.某服装批发市场销售种衬衫,村衫每件进货价为50元,规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/件)
60
65
70
销售量y(件)
1400
1300
1200
(1)求出y与x之间的函数表达式;(不需
要求自变量x的取值范围)
(2)该批发市场每月想从这种衬杉销售中获利24000元,又想尽量给客户实惠,该如何给这种村衫定价?
(3)物价部门规定,该衬杉的每件利润不允许高于进货价的30%,设这种衬杉每月的总利润为w(元),那么售价定为多少元可获得最大利润?最大利润是多少?
八、(本题满分
14分)
23、如图,△ABC中,AB=AC,AB⊥AC,点D、E分别是BC、AC的中点,AF⊥BE与点F。
(1)求证:AE2=FE·BE;
(2)求∠AFC的大小;
(3)若DF=2,求△ABF的面积;
合肥庐阳区四十五中2020-2021第一学期九年级期中数学试卷答案
1
2
3
4
5
6
7
8
9
10
A
A
B
B
C
D
D
A
B
B
11、
12;
12、
2020;
13、
12;
14、
或;
15、;
16、
17、(1)y=(x-1)2-4;(1,-4);(2)-4≤y<0;
18、
19、
20、
21、(1)b=3;
k=-2;
(2)(0,);
(3)x>-2或-1<x<0;
22、(1)y=-20x+2600;
(2)70;
(3)售价定为65元时,最大利润19500元;
23、(1)∵AF⊥BE,AB⊥AC,∴∠AFE=∠BAE=90°,∠AEF=∠BEA,∴△AEF∽△BEA,∴AE2=FE·BE;
(2)135°;
(3)2;
同课章节目录
