27.2.1 第1课时相似三角形的判定(1) 课件(共33张PPT)
文档属性
| 名称 | 27.2.1 第1课时相似三角形的判定(1) 课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 17:37:54 | ||
图片预览








文档简介
(共33张PPT)
第二节
相似三角形
第一课时
相似三角形的判定(1)
人教版
九年级数学下册
教学课件
第二十七章
相似
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
2.相似多边形中,最简单的就是相似三角形.如果
∠A
=∠A1,∠B=∠B1,∠C=∠C1,
=
=
,那么△ABC与△A1B1C1相似
吗?我们还有其他方法判定两个三角形相似吗?
1.
相似多边形的对应角
,对应边
,对
应边的比叫做
.
相等
成比例
相似比
情景导学
第二部分
新课目标
新课目标
1.
理解相似三角形的概念.
2.
理解平行线分线段成比例的基本事实及其推论,掌
握相似三角形判定定理的预备定理的有关证明.
3.
掌握平行线分线段成比例的基本事实及其推论的应
用,会用平行线判定两个三角形相似并进行证明和
计算.
第三部分
新课进行时
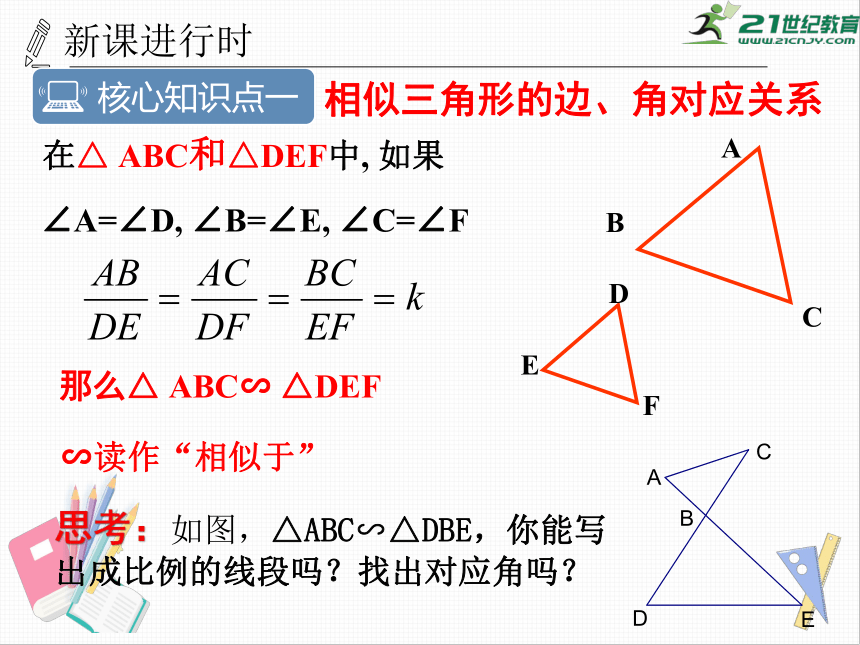
在△
ABC和△DEF中,
如果
A
B
C
D
E
F
∠A=∠D,
∠B=∠E,
∠C=∠F
那么△
ABC∽
△DEF
∽读作“相似于”
思考:如图,△ABC∽△DBE,你能写出成比例的线段吗?找出对应角吗?
新课进行时
核心知识点一
相似三角形的边、角对应关系
小组讨论1:“∽”与“相似”有什么区别和联系?相似三角形的定义是什么?由此得到相似三角形的性质又是什么?
【反思小结】当两个相似三角形用符号“∽”表示时,对应顶点已经给出,即相应位置上的点是对应点,由对应点可以写出对应角、对应边.一般地,最大边与最大边是对应边;最大角与最大角是对应角,公共角或对顶角是对应角;对应边的对角是对应角,对应角的对边是对应边.
新课进行时
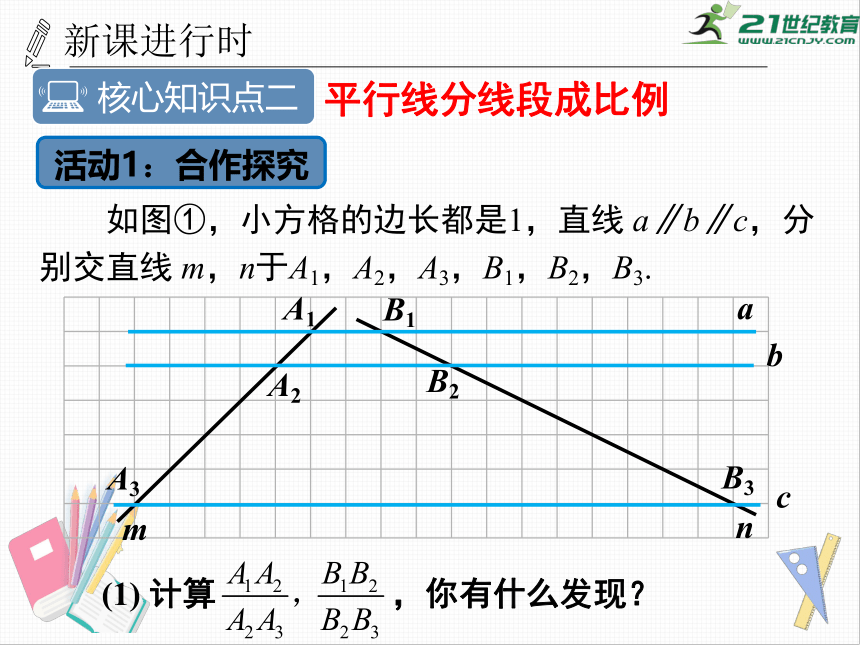
如图①,小方格的边长都是1,直线
a∥b∥c,分别交直线
m,n于A1,A2,A3,B1,B2,B3.
活动1:合作探究
A1
A2
A3
B1
B2
B3
m
n
a
b
c
(1)
计算
,你有什么发现?
新课进行时
核心知识点二
平行线分线段成比例
(2)
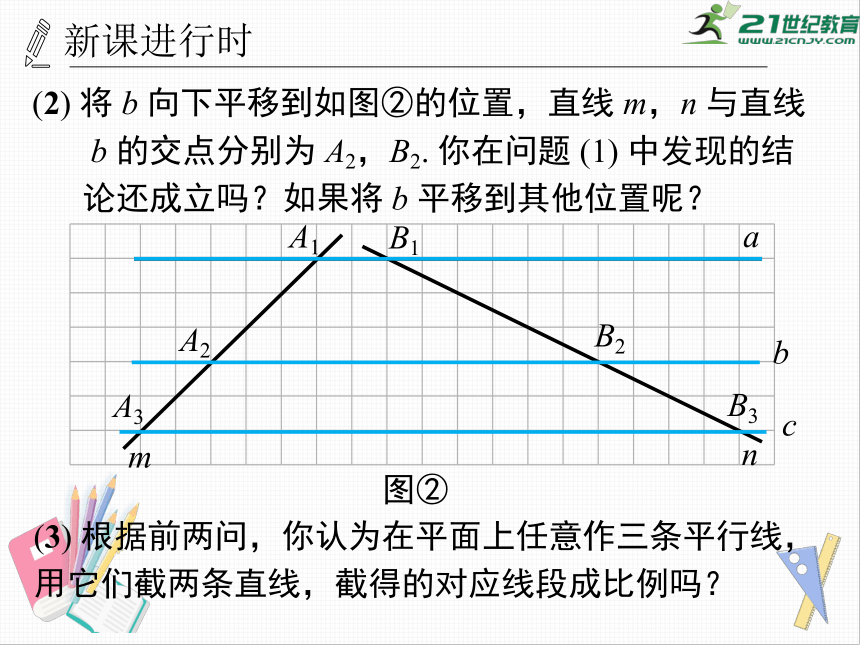
将
b
向下平移到如图②的位置,直线
m,n
与直线
b
的交点分别为
A2,B2.
你在问题
(1)
中发现的结
论还成立吗?如果将
b
平移到其他位置呢?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图②
(3)
根据前两问,你认为在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
新课进行时
一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
符号语言
若a∥b∥
c
,则
思考
A1
A2
A3
B1
B2
B3
b
c
a
1.
如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
归纳
新课进行时
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线
n
向左平移到
B1
与A1
重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
活动2
新课进行时
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线
n
向左平移到
B2
与A2
重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
新课进行时
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳
平行线分线段成比例的推论
新课进行时
活动3
如图,在△ABC中,D为AB边的中点,过点D作BC的平行线DE,交AC于点E.
问题1
:△ADE与△ABC的三个角分别相等吗?
问题2
:分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?
B
C
A
D
E
新课进行时
核心知识点三
相似三角形的判定的预备定理
这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似,相似比为
先证明两个三角形的对应角相等.
在△ADE与△ABC中,∠A=∠A
∵DE∥BC
∴∠ADE=∠B,∠AED=∠C
再证明两个三角形的对应边的比相等.
过点E作EF∥AB,EF交BC于点F.
在
BFED中,DE=BF,DB=EF
∵AD=BD=
AB
∴AD=EF
又∠A=∠1,∠2=∠C
∴△ADE≌△EFC
∴AE=EC=
AC
DE=FC=BF=
BC
A
B
C
D
E
F
1
2
新课进行时
1:2
A
B
C
D
E
改变点D在AB上的位置,继续观察图形,进一步想
△ADE与△ABC是否存在着相似关系.
F
证明:在
△ADE与
△ABC中,∠A=∠A.
∵
DE∥BC,∴
∠ADE=∠B,∠AED=∠C.
如图,过点
D
作
DF∥AC,交
BC
于点
F.
∵
DE∥BC,DF∥AC,
∴
∵
四边形DFCE为平行四边形
∴
DE=FC,
∴△ADE∽△ABC.
∴
新课进行时
由此我们得到判定三角形相似的定理:
平行于三角形一边的直线与其他两边相交,
所构成的三角形与原三角形相似.
符号语言表示:
∵DE∥BC,
∴△ADE∽△ABC
新课进行时
A
B
C
D
E
第四部分
知识小结
知识小结
?推论
?相似三角形判定的预备定理
?平行线分线段成比例定理
平行线分线段成比例
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
易错点
思想方法小结:
由
特殊到一般、数形结合的数学思想
第五部分
随堂演练
如图,AD∥EF∥BC,下列比例式不成立的是
(
)
A.
=
B.
=
C.
=
D.
=
C
随堂演练
2.
如图,在△ABC中,DE∥BC,小聪认为:
∵DE∥BC,∴
=
;小明认为应是:
∵DE∥BC,∴△ADE∽△ABC,∴
=
那么你认为(
)
A.仅小聪对
B.仅小明对
C.两人均对
D.两人均错
AD
AB
DE
BC
AD
AB
DE
BC
B
随堂演练
3.
如图,若△ABC∽△DEF,则∠A的度数为
______,DF=______.
105°
3
4.
如图,已知AB是⊙O的直径,C是AB延长线
上一点,BC=OB,CE是⊙O的切线,切点为
D,过点A作AE⊥CE,垂足为E,则
CD∶DE的值是_______.
2
随堂演练
随堂演练
5.
已知△ABC∽△A′B′C′,相似比为3∶5,且∠A=60°,∠B=36°,则△A′B′C′与△ABC的相似比为______,∠C′=______°.
6.
如图,△ABC∽△CDE,B,C,D三点在一条直线上,AB=6,BC=2,DE=4,求BD的长.
3:5
84
解:BD的长为14.
7.
如图,在△ABC中,DE∥BC,则△____∽△____,
对应边的比例式为
=
=
ADE
ABC
——
——.
8.
如图,在△ABC中,EF∥BC,AE=2cm,
BE=6cm,BC=4cm,EF的长为_______.
1cm
随堂演练
AE
AC
DE
BC
AD
AB
10.
如图,在□ABCD中,EF∥AB,
DE∶EA=2∶3,EF=4,求CD的长.
解:CD的长为10.
9.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么
DG:BC=_____。
A
B
C
D
E
F
G
H
I
1:4
随堂演练
11.
如图,在△ABC中,
EF∥BC.
(1)
如果E、F分别是
AB
和
AC
上的点,
AE
=
BE=7,
FC
=
4
,那么
AF
的长是多少?
A
B
C
E
F
解:∵
∴
解得
AF
=
4.
(2)
如果AB
=
10,AE=6,AF
=
5,那么
FC
的长是多少?
解:∵
∴
解得
AC
=
.
∴
FC
=
AC-AF
=
.
随堂演练
12.
如图,已知菱形
ABCD
内接于△AEF,AE=5cm,
AF
=
4
cm,求菱形的边长.
解:∵
四边形
ABCD
为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为
x
cm,则CD
=
AD
=
x
cm,DF
=
(4-x)
cm.
∴
解得
x
=
∴菱形的边长为
cm.
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
第二节
相似三角形
第一课时
相似三角形的判定(1)
人教版
九年级数学下册
教学课件
第二十七章
相似
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
2.相似多边形中,最简单的就是相似三角形.如果
∠A
=∠A1,∠B=∠B1,∠C=∠C1,
=
=
,那么△ABC与△A1B1C1相似
吗?我们还有其他方法判定两个三角形相似吗?
1.
相似多边形的对应角
,对应边
,对
应边的比叫做
.
相等
成比例
相似比
情景导学
第二部分
新课目标
新课目标
1.
理解相似三角形的概念.
2.
理解平行线分线段成比例的基本事实及其推论,掌
握相似三角形判定定理的预备定理的有关证明.
3.
掌握平行线分线段成比例的基本事实及其推论的应
用,会用平行线判定两个三角形相似并进行证明和
计算.
第三部分
新课进行时
在△
ABC和△DEF中,
如果
A
B
C
D
E
F
∠A=∠D,
∠B=∠E,
∠C=∠F
那么△
ABC∽
△DEF
∽读作“相似于”
思考:如图,△ABC∽△DBE,你能写出成比例的线段吗?找出对应角吗?
新课进行时
核心知识点一
相似三角形的边、角对应关系
小组讨论1:“∽”与“相似”有什么区别和联系?相似三角形的定义是什么?由此得到相似三角形的性质又是什么?
【反思小结】当两个相似三角形用符号“∽”表示时,对应顶点已经给出,即相应位置上的点是对应点,由对应点可以写出对应角、对应边.一般地,最大边与最大边是对应边;最大角与最大角是对应角,公共角或对顶角是对应角;对应边的对角是对应角,对应角的对边是对应边.
新课进行时
如图①,小方格的边长都是1,直线
a∥b∥c,分别交直线
m,n于A1,A2,A3,B1,B2,B3.
活动1:合作探究
A1
A2
A3
B1
B2
B3
m
n
a
b
c
(1)
计算
,你有什么发现?
新课进行时
核心知识点二
平行线分线段成比例
(2)
将
b
向下平移到如图②的位置,直线
m,n
与直线
b
的交点分别为
A2,B2.
你在问题
(1)
中发现的结
论还成立吗?如果将
b
平移到其他位置呢?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图②
(3)
根据前两问,你认为在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
新课进行时
一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
符号语言
若a∥b∥
c
,则
思考
A1
A2
A3
B1
B2
B3
b
c
a
1.
如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
归纳
新课进行时
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线
n
向左平移到
B1
与A1
重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
活动2
新课进行时
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线
n
向左平移到
B2
与A2
重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
新课进行时
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
归纳
平行线分线段成比例的推论
新课进行时
活动3
如图,在△ABC中,D为AB边的中点,过点D作BC的平行线DE,交AC于点E.
问题1
:△ADE与△ABC的三个角分别相等吗?
问题2
:分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?
B
C
A
D
E
新课进行时
核心知识点三
相似三角形的判定的预备定理
这样,我们证明了△ADE和△ABC的对应角相等,对应边的比相等,所以它们相似,相似比为
先证明两个三角形的对应角相等.
在△ADE与△ABC中,∠A=∠A
∵DE∥BC
∴∠ADE=∠B,∠AED=∠C
再证明两个三角形的对应边的比相等.
过点E作EF∥AB,EF交BC于点F.
在
BFED中,DE=BF,DB=EF
∵AD=BD=
AB
∴AD=EF
又∠A=∠1,∠2=∠C
∴△ADE≌△EFC
∴AE=EC=
AC
DE=FC=BF=
BC
A
B
C
D
E
F
1
2
新课进行时
1:2
A
B
C
D
E
改变点D在AB上的位置,继续观察图形,进一步想
△ADE与△ABC是否存在着相似关系.
F
证明:在
△ADE与
△ABC中,∠A=∠A.
∵
DE∥BC,∴
∠ADE=∠B,∠AED=∠C.
如图,过点
D
作
DF∥AC,交
BC
于点
F.
∵
DE∥BC,DF∥AC,
∴
∵
四边形DFCE为平行四边形
∴
DE=FC,
∴△ADE∽△ABC.
∴
新课进行时
由此我们得到判定三角形相似的定理:
平行于三角形一边的直线与其他两边相交,
所构成的三角形与原三角形相似.
符号语言表示:
∵DE∥BC,
∴△ADE∽△ABC
新课进行时
A
B
C
D
E
第四部分
知识小结
知识小结
?推论
?相似三角形判定的预备定理
?平行线分线段成比例定理
平行线分线段成比例
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
易错点
思想方法小结:
由
特殊到一般、数形结合的数学思想
第五部分
随堂演练
如图,AD∥EF∥BC,下列比例式不成立的是
(
)
A.
=
B.
=
C.
=
D.
=
C
随堂演练
2.
如图,在△ABC中,DE∥BC,小聪认为:
∵DE∥BC,∴
=
;小明认为应是:
∵DE∥BC,∴△ADE∽△ABC,∴
=
那么你认为(
)
A.仅小聪对
B.仅小明对
C.两人均对
D.两人均错
AD
AB
DE
BC
AD
AB
DE
BC
B
随堂演练
3.
如图,若△ABC∽△DEF,则∠A的度数为
______,DF=______.
105°
3
4.
如图,已知AB是⊙O的直径,C是AB延长线
上一点,BC=OB,CE是⊙O的切线,切点为
D,过点A作AE⊥CE,垂足为E,则
CD∶DE的值是_______.
2
随堂演练
随堂演练
5.
已知△ABC∽△A′B′C′,相似比为3∶5,且∠A=60°,∠B=36°,则△A′B′C′与△ABC的相似比为______,∠C′=______°.
6.
如图,△ABC∽△CDE,B,C,D三点在一条直线上,AB=6,BC=2,DE=4,求BD的长.
3:5
84
解:BD的长为14.
7.
如图,在△ABC中,DE∥BC,则△____∽△____,
对应边的比例式为
=
=
ADE
ABC
——
——.
8.
如图,在△ABC中,EF∥BC,AE=2cm,
BE=6cm,BC=4cm,EF的长为_______.
1cm
随堂演练
AE
AC
DE
BC
AD
AB
10.
如图,在□ABCD中,EF∥AB,
DE∶EA=2∶3,EF=4,求CD的长.
解:CD的长为10.
9.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么
DG:BC=_____。
A
B
C
D
E
F
G
H
I
1:4
随堂演练
11.
如图,在△ABC中,
EF∥BC.
(1)
如果E、F分别是
AB
和
AC
上的点,
AE
=
BE=7,
FC
=
4
,那么
AF
的长是多少?
A
B
C
E
F
解:∵
∴
解得
AF
=
4.
(2)
如果AB
=
10,AE=6,AF
=
5,那么
FC
的长是多少?
解:∵
∴
解得
AC
=
.
∴
FC
=
AC-AF
=
.
随堂演练
12.
如图,已知菱形
ABCD
内接于△AEF,AE=5cm,
AF
=
4
cm,求菱形的边长.
解:∵
四边形
ABCD
为菱形,
B
C
A
D
E
F
∴CD∥AB,
∴
设菱形的边长为
x
cm,则CD
=
AD
=
x
cm,DF
=
(4-x)
cm.
∴
解得
x
=
∴菱形的边长为
cm.
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
