27.2.1 第2课时相似三角形的判定(2) 课件(共29张PPT)
文档属性
| 名称 | 27.2.1 第2课时相似三角形的判定(2) 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
第二十七章
相似
第二节
相似三角形
第二课时
相似三角形的判定(2)
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
不需要
能
第二部分
新课目标
新课目标
1.掌握相似三角形的判定定理:“三边成比例的两个三角形相似”,“两边成比例且夹角相等的两个三角形相似”.
2.会进行简单的证明、计算.
教学重点:利用相似三角形的判定定理1、2计算与证明.
教学难点:利用相似三角形的判定定理1、2计算与证明.
第三部分
新课进行时
新课进行时
核心知识点一
三边成比例的两个三角形相似
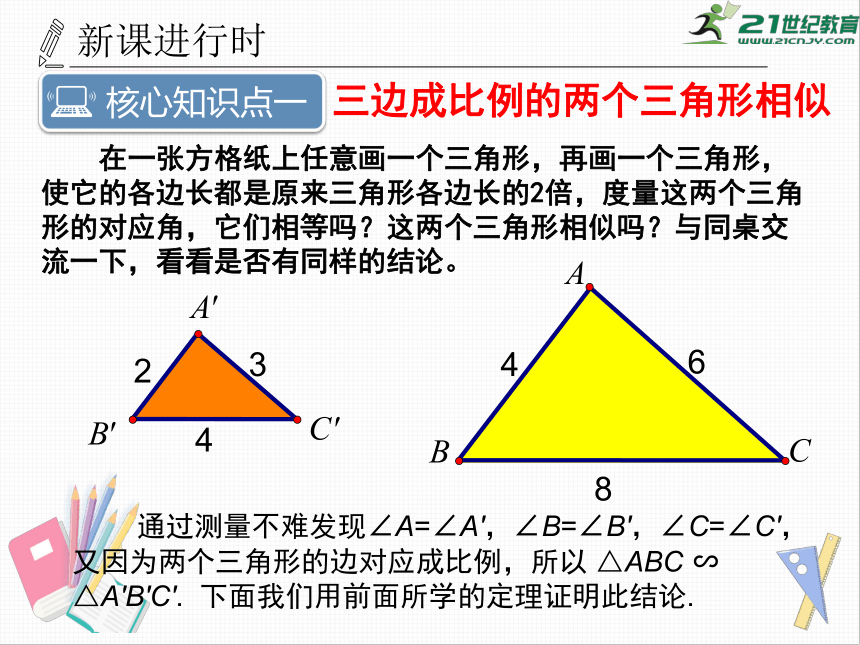
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的2倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论。
C′
B′
A′
A
B
C
2
3
4
4
6
8
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',
又因为两个三角形的边对应成比例,所以
△ABC
∽
△A′B′C′.
下面我们用前面所学的定理证明此结论.
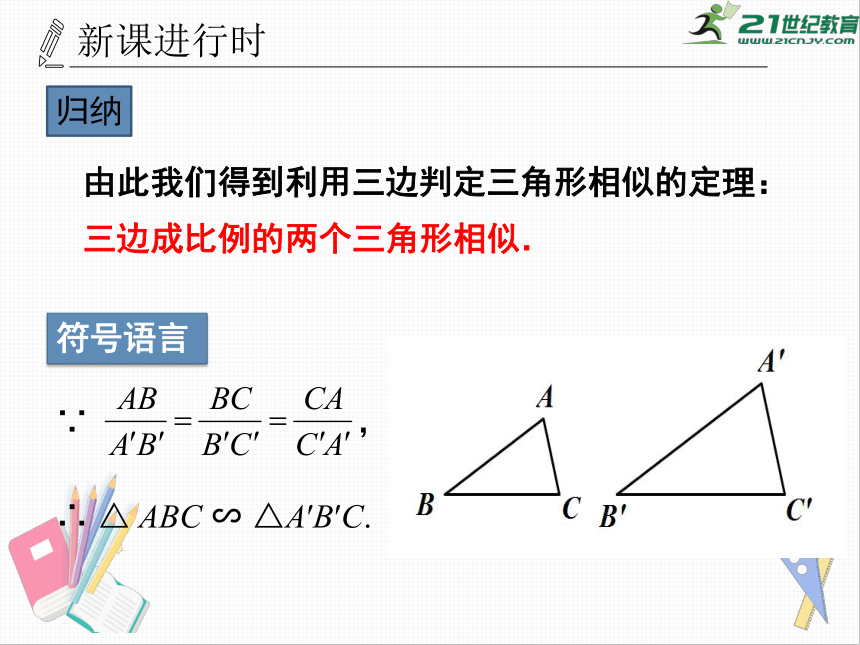
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
归纳
∵
,
∴
△
ABC
∽
△A′B′C.
符号语言
新课进行时
例1
判断图中的两个三角形是否相似,并说明理由.
A
B
C
3
3.5
4
D
F
E
1.8
2.1
2.4
如何利用三边成比例判定两个三角形相似?
∵
,
,
,
∴
.
∴
△ABC
∽
△DEF.
解:
反思小结:利用三边成比例判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
新课进行时
思考
新课进行时
核心知识点一
两边成比例及夹角对应相等的两个三角形相似
利用刻度尺和量角器画
△ABC和
△A′B′C′,使
∠A=∠A′,
量出
BC
及
B′C′
的长,
它们的比值等于
k
吗?再量一量两个三角形另外的
两个角,你有什么发现?△ABC
与
△A′B′C′
有何关
系?
两个三角形相似
改变
k
和∠A
的值的大小,是否有同样的结论?
如何证明?
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A=
∠A′,
证明:在
△A′B′C′
的边
A′B′
上截取点D,使
A′D
=
AB.过点
D
作
DE∥B′C′,交
A′C′
于点
E.
∵
DE∥B′C′,
∴
△A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∵
A′D=AB,
∴
∴
A′E
=
AC
.
又
∠A′
=
∠A.
∴
△A′DE
≌
△ABC,
∴
△A′B′C′
∽
△ABC.
新课进行时
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言
∵
∠A=∠A′,
B
A
C
B'
A'
C'
∴
△ABC
∽
△A′B′C′
.
归纳
新课进行时
对于△ABC和△A'B'C',如果
,∠B=∠B',这两个三角形一定相似吗?试着画画看.
不
一
定
相
似
注意:如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角。
新课进行时
根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;
(2)AB=4cm,BC=6cm,AC=8cm.
'B'=12cm,B'C'=18cm,A'C'=21cm
解:(1)∵
又
∠A=∠A'
∴
△ABC∽△A'B'C'
(2)∵
△ABC与△A'B'C'的三组对应边的比不等,它们不相似
两三角形的相似比是多少?
新课进行时
要使两三角形相似,不改变AC的长,A'C'的长应当改为多少?
第四部分
知识小结
知识小结
相似三角形的判定定理
?三边成比例的两个三角形相似
?两边成比例,且夹角相等的两个三角形相似
思想方法小结:
由
特殊到一般、转化的数学思想
第五部分
随堂演练
随堂演练
1.
如图,若
=
=
,则△______∽△______;
2.
若一个三角形的三边长分别为6cm,9cm,
7.5cm,另一个三角形的三边长分别为12cm,
18cm,________时,这两个三角形相似.
ADE
ABC
15cm
3.
根据下面条件,判断△ABC与△A′B′C′
是否相似,并说明理由.
∠A=120°,AB=7cm,AC=14cm;
∠A=120°,A′B′=3cm,A′C′=6cm.
随堂演练
解:∵
,
,
∴
.
又∠A=∠A′,∴△ABC∽△A′B′C′.
AB
A'B'
7
3
=
AC
A'C'
14
6
=
=
7
3
AB
A'B'
AC
A'C'
=
4.
如图,△ABC
与
△ADE
都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.
求证:△ABC
∽△ADE.
证明:
∵
△ABC
与
△ADE
是等腰三角形,
∴
AD
=AE,AB
=
AC,
∴
又
∵∠DAB
=
∠CAE,
∴
∠DAB
+∠BAE
=
∠CAE
+∠BAE,
即
∠DAE
=∠BAC,∴△ABC
∽
△ADE.
A
B
C
D
E
随堂演练
5.(1)根据下面条件,判断△ABC与△A′B′C′是否
相似,并说明理由.
AB=4cm,BC=6cm,AC=8cm,
A′B′=12cm,B′C′=18cm,A′C′=
21cm.
(2)若(1)中两三角形不相似,那么要使它们相似,
不改变AC的长,A′C′的长应当改为多少?
解:(1)△ABC与△A′B′C′的三组对应边的比不等,它们不相似.
(2)当A′C′=24cm时,两个三角形相似.
随堂演练
6.
如图,在△ABC中,D,E分别是AB,AC上的点,AB=7.8,BD=4.8,AC=6,AE=3.9,试判断△ADE与△ABC是否相似,某同学的解答如下:
解:∵AB=AD+BD,而AB=7.8,BD=4.8,
∴AD=7.8-4.8=3.
∵
∴这两个三角形不相似.
你同意他的判断吗?请说明理由.
AD
AB
≠
AE
AC
随堂演练
随堂演练
3
6
解:他的判断是错误的.
∵AB=AD+BD,而AB=7.8,BD=4.8,
∴AD=7.8-4.8=3.
∵
,
,
∴
.
又∵∠A=∠A,
∴△ADE∽△ACB
.
=
=
=
=
=
AD
AC
AD
AC
AE
AB
AE
AB
1
2
1
2
3.9
7.8
7.
如图,△ABC中,点
D,E,F
分别是
AB,BC,CA
的中点,求证:△ABC∽△EFD.
∴△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
第二十七章
相似
第二节
相似三角形
第二课时
相似三角形的判定(2)
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是对所有的对应角和对应边都要一一验证呢?
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
不需要
能
第二部分
新课目标
新课目标
1.掌握相似三角形的判定定理:“三边成比例的两个三角形相似”,“两边成比例且夹角相等的两个三角形相似”.
2.会进行简单的证明、计算.
教学重点:利用相似三角形的判定定理1、2计算与证明.
教学难点:利用相似三角形的判定定理1、2计算与证明.
第三部分
新课进行时
新课进行时
核心知识点一
三边成比例的两个三角形相似
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的2倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论。
C′
B′
A′
A
B
C
2
3
4
4
6
8
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',
又因为两个三角形的边对应成比例,所以
△ABC
∽
△A′B′C′.
下面我们用前面所学的定理证明此结论.
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
归纳
∵
,
∴
△
ABC
∽
△A′B′C.
符号语言
新课进行时
例1
判断图中的两个三角形是否相似,并说明理由.
A
B
C
3
3.5
4
D
F
E
1.8
2.1
2.4
如何利用三边成比例判定两个三角形相似?
∵
,
,
,
∴
.
∴
△ABC
∽
△DEF.
解:
反思小结:利用三边成比例判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
新课进行时
思考
新课进行时
核心知识点一
两边成比例及夹角对应相等的两个三角形相似
利用刻度尺和量角器画
△ABC和
△A′B′C′,使
∠A=∠A′,
量出
BC
及
B′C′
的长,
它们的比值等于
k
吗?再量一量两个三角形另外的
两个角,你有什么发现?△ABC
与
△A′B′C′
有何关
系?
两个三角形相似
改变
k
和∠A
的值的大小,是否有同样的结论?
如何证明?
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A=
∠A′,
证明:在
△A′B′C′
的边
A′B′
上截取点D,使
A′D
=
AB.过点
D
作
DE∥B′C′,交
A′C′
于点
E.
∵
DE∥B′C′,
∴
△A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∵
A′D=AB,
∴
∴
A′E
=
AC
.
又
∠A′
=
∠A.
∴
△A′DE
≌
△ABC,
∴
△A′B′C′
∽
△ABC.
新课进行时
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言
∵
∠A=∠A′,
B
A
C
B'
A'
C'
∴
△ABC
∽
△A′B′C′
.
归纳
新课进行时
对于△ABC和△A'B'C',如果
,∠B=∠B',这两个三角形一定相似吗?试着画画看.
不
一
定
相
似
注意:如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角。
新课进行时
根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;
(2)AB=4cm,BC=6cm,AC=8cm.
'B'=12cm,B'C'=18cm,A'C'=21cm
解:(1)∵
又
∠A=∠A'
∴
△ABC∽△A'B'C'
(2)∵
△ABC与△A'B'C'的三组对应边的比不等,它们不相似
两三角形的相似比是多少?
新课进行时
要使两三角形相似,不改变AC的长,A'C'的长应当改为多少?
第四部分
知识小结
知识小结
相似三角形的判定定理
?三边成比例的两个三角形相似
?两边成比例,且夹角相等的两个三角形相似
思想方法小结:
由
特殊到一般、转化的数学思想
第五部分
随堂演练
随堂演练
1.
如图,若
=
=
,则△______∽△______;
2.
若一个三角形的三边长分别为6cm,9cm,
7.5cm,另一个三角形的三边长分别为12cm,
18cm,________时,这两个三角形相似.
ADE
ABC
15cm
3.
根据下面条件,判断△ABC与△A′B′C′
是否相似,并说明理由.
∠A=120°,AB=7cm,AC=14cm;
∠A=120°,A′B′=3cm,A′C′=6cm.
随堂演练
解:∵
,
,
∴
.
又∠A=∠A′,∴△ABC∽△A′B′C′.
AB
A'B'
7
3
=
AC
A'C'
14
6
=
=
7
3
AB
A'B'
AC
A'C'
=
4.
如图,△ABC
与
△ADE
都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.
求证:△ABC
∽△ADE.
证明:
∵
△ABC
与
△ADE
是等腰三角形,
∴
AD
=AE,AB
=
AC,
∴
又
∵∠DAB
=
∠CAE,
∴
∠DAB
+∠BAE
=
∠CAE
+∠BAE,
即
∠DAE
=∠BAC,∴△ABC
∽
△ADE.
A
B
C
D
E
随堂演练
5.(1)根据下面条件,判断△ABC与△A′B′C′是否
相似,并说明理由.
AB=4cm,BC=6cm,AC=8cm,
A′B′=12cm,B′C′=18cm,A′C′=
21cm.
(2)若(1)中两三角形不相似,那么要使它们相似,
不改变AC的长,A′C′的长应当改为多少?
解:(1)△ABC与△A′B′C′的三组对应边的比不等,它们不相似.
(2)当A′C′=24cm时,两个三角形相似.
随堂演练
6.
如图,在△ABC中,D,E分别是AB,AC上的点,AB=7.8,BD=4.8,AC=6,AE=3.9,试判断△ADE与△ABC是否相似,某同学的解答如下:
解:∵AB=AD+BD,而AB=7.8,BD=4.8,
∴AD=7.8-4.8=3.
∵
∴这两个三角形不相似.
你同意他的判断吗?请说明理由.
AD
AB
≠
AE
AC
随堂演练
随堂演练
3
6
解:他的判断是错误的.
∵AB=AD+BD,而AB=7.8,BD=4.8,
∴AD=7.8-4.8=3.
∵
,
,
∴
.
又∵∠A=∠A,
∴△ADE∽△ACB
.
=
=
=
=
=
AD
AC
AD
AC
AE
AB
AE
AB
1
2
1
2
3.9
7.8
7.
如图,△ABC中,点
D,E,F
分别是
AB,BC,CA
的中点,求证:△ABC∽△EFD.
∴△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
