27.2.1 第3课时相似三角形的判定(3) 课件(共31张PPT)
文档属性
| 名称 | 27.2.1 第3课时相似三角形的判定(3) 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 17:39:53 | ||
图片预览






文档简介
(共31张PPT)
第二十七章
相似
第二节
相似三角形
第三课时
相似三角形的判定(3)
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
观察三角尺,其中同样角度(30°与60°)的两个三角尺大小不同,它们一定相似吗?
一定相似
第二部分
新课目标
新课目标
1.掌握相似三角形的判定定理:“如果一个三角
形的两个角与另一个三角形的两个角对应相
等,那么这两个三角形相似”.
2.了解“斜边的比等于一组直角边的比的两相直
角三角形相似”.
3.
会进行简单的证明、计算.
第三部分
新课进行时
新课进行时
核心知识点一
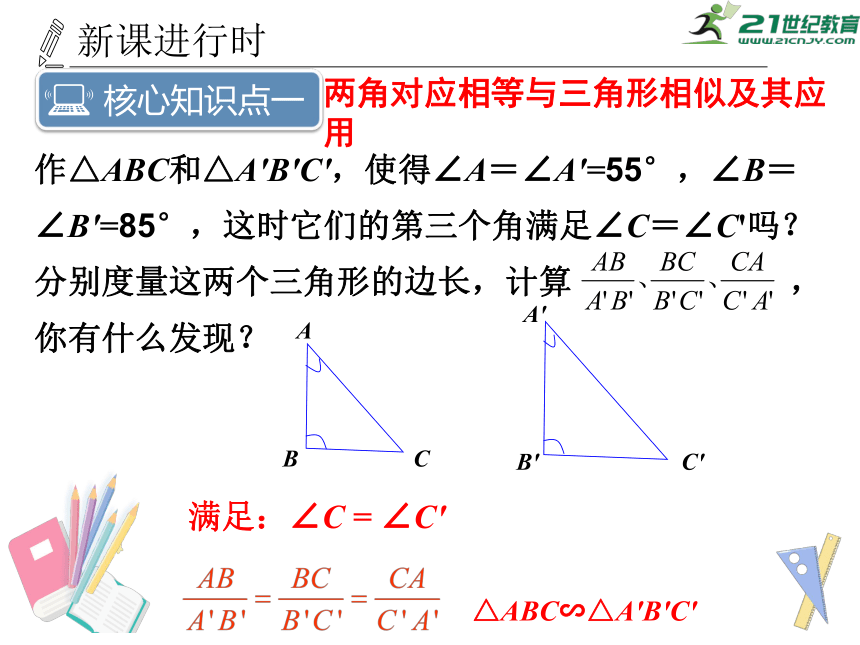
两角对应相等与三角形相似及其应用
作△ABC和△A'B'C',使得∠A=∠A'=55°,∠B=∠B'=85°,这时它们的第三个角满足∠C=∠C'吗?分别度量这两个三角形的边长,计算
,你有什么发现?
A
B
C
A'
B'
C'
满足:∠C
=
∠C'
△ABC∽△A'B'C'
证明:在
△ABC
的边
AB(或
AB
的延长线)上,截取
AD=A′B′,过点
D
作
DE
//
BC,交
AC
于点
E,则有△ADE
∽△ABC,∠ADE
=∠B.
∵∠B=∠B′,
∴∠ADE=∠B′.
又∵
AD=A′B′,∠A=∠A′,
∴△ADE
≌△A′B′C′,
∴△A′B′C′
∽△ABC.
C
A
A'
B
B'
C'
D
E
如何证明△A′B′C′∽△ABC?
新课进行时
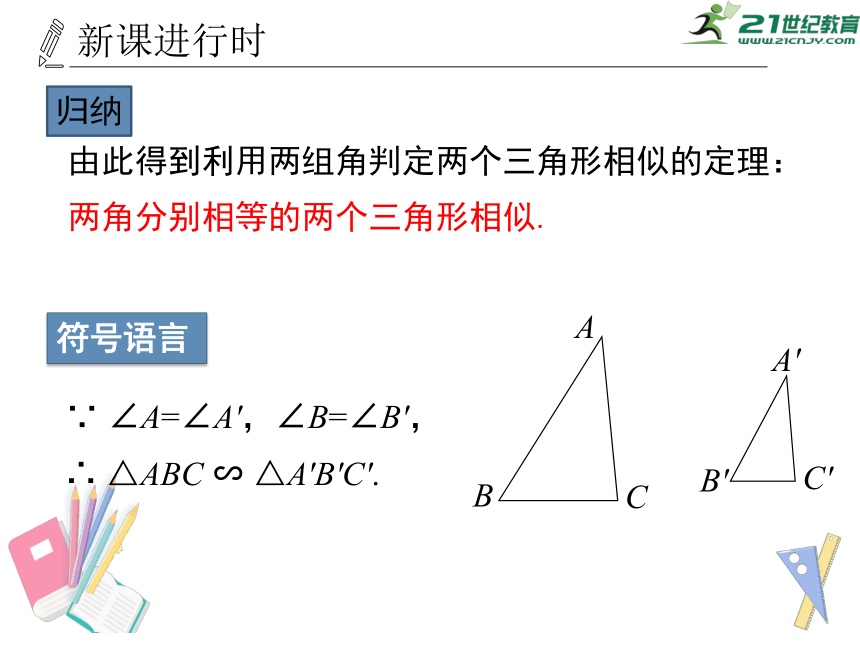
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵
∠A=∠A',∠B=∠B',
∴
△ABC
∽
△A'B'C'.
C
A
B
A'
B'
C'
新课进行时
归纳
符号语言
证明:∵
在△
ABC中,∠A=40
°
,
∠B=80
°
,
∴
∠C=180
°-∠A-∠B=60
°.
∵
在△DEF中,∠E=80
°,
∠F=60
°.
∴
∠B=∠E,∠C=∠F.
∴
△ABC
∽△DEF.
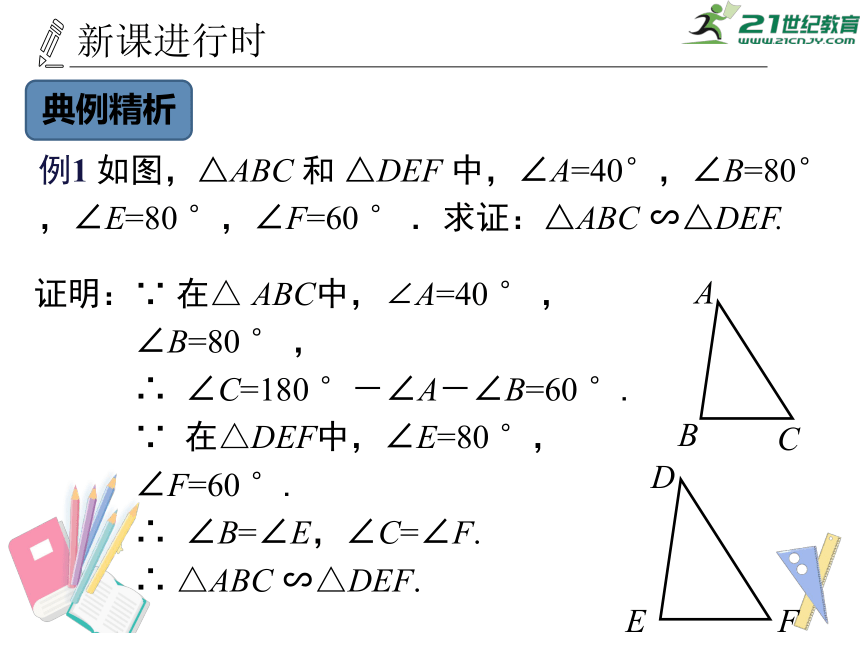
例1
如图,△ABC
和
△DEF
中,∠A=40°,∠B=80°,∠E=80
°,∠F=60
°
.求证:△ABC
∽△DEF.
A
C
B
F
E
D
典例精析
新课进行时
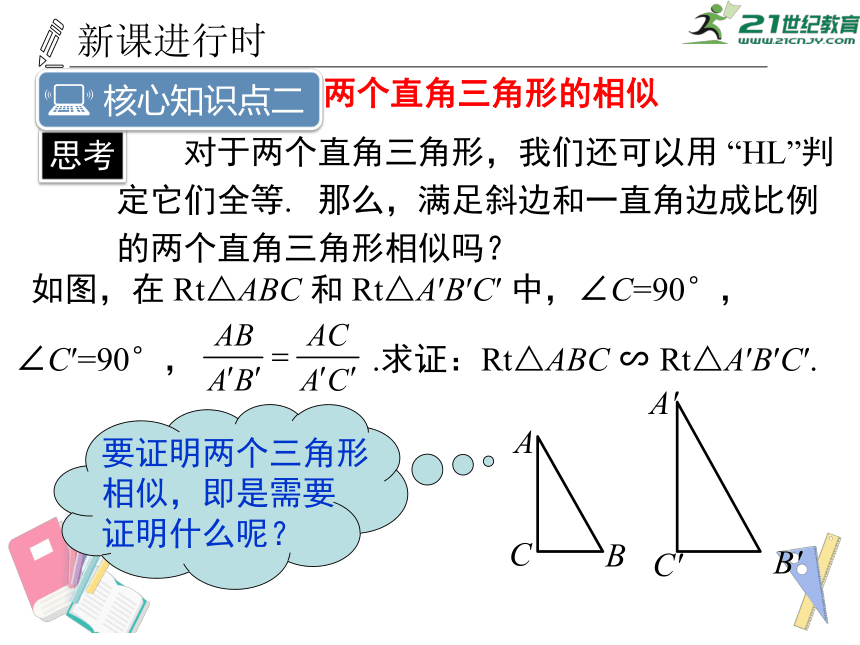
对于两个直角三角形,我们还可以用
“HL”判定它们全等.
那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
思考
如图,在
Rt△ABC
和
Rt△A′B′C′
中,∠C=90°,
∠C′=90°,
.求证:Rt△ABC
∽
Rt△A′B′C′.
C
A
A'
B
B'
C'
要证明两个三角形相似,即是需要
证明什么呢?
新课进行时
核心知识点二
两个直角三角形的相似
证明:设____________=
k
,则AB=kA′B′,AC=kA′B′.
由
,得
∴
________.
∴
Rt
△ABC
∽
Rt
△A′B′C′.
勾股定理
∴
C
A
A'
B
B'
C'
新课进行时
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,
那么这两个直角三角形相似。
直角三角形相似的定理之HL
A
B
C
△ABC∽△A1B1C1
A1
B1
C1
在Rt△ABC
和
Rt△A1B1C1中
新课进行时
符号语言
例2
如图,Rt△ABC中∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长.
解:∵
ED⊥AB,∠C=90°,
∴∠EDA=∠C
又∠A=
∠A
∴△AED∽△ABC
D
A
B
C
E
思考:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.图中有哪几对相似三角形?为什么?
分析:∵CD⊥AB,∴∠CDB=90°.
∴∠B+∠BCD=90°.
又∵∠ACB=90°,∴∠B+∠A=90°.∴∠BCD=∠A
在△ABC和△CBD中,∵∠ACB=∠CDB=90°,∠BCD=∠A,∴△ABC∽△CBD.
请你再找出其他的几对相似三角形:
△ABC∽△ACD
△CBD∽△ACD
思考:1.根据以上结论,你发现了什么?
2.直角三角形相似的判定有哪些?
新课进行时
小组讨论:如何根据题目特点灵活选用本节所学相似三角形的判定方法?
证两三角形相似,若已具备一组角对应相等,则应先考虑“两角对应相等的两个三角形相似”这一判定方法,而找等角时常用到公共角、对顶角、等角(或同角)的余角相等等一些隐含条件.判定直角三角形相似时,可以用其相似独有的判定方法,也可以用一般三角形相似的判定方法.不过,更多的时候是用两角相等来证.
【反思小结】
新课进行时
第四部分
知识小结
知识小结
两角分别相等的两个三角形相似
利用两角判定三角形相似
直角三角形相似的判定
思想方法小结:
类比、转化的数学思想
第五部分
随堂演练
1.
在
Rt△ABC
和
Rt△A′B′C′
中,∠C=∠C′=90°,依据下列各组条件判定这两个三角形是否相似.
(1)
∠A=35°,∠B′=55°.
;
(2)
AC=3,BC=4,A′C′=6,B′C′=8.
;
(3)
AB=10,AC=8,A′B′=25,B′C′=15.
.
相似
相似
相似
随堂演练
2.下列结论:
①所有的等腰三角形都相似,
②有一个角是80°的两个等腰三角形相似,
③有一个角是100°的两个等腰三角形相似,
④有一个角相等的两个等腰三角形相似,其中
正确的有(
)
A.1个
B.2个
C.3个
D.4个
A
3.如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3,则
的值为
( )
B
A.
B.
C.
D.
随堂演练
4.如图,在Rt△ABC中,
∠ACB=90°,CD是斜边AB上的高.
(1)
若AD=8,BD=2,则CD=
;
(2)
若BD=4,AB=9,则BC=
;
(3)
若AD=2,AB=3,则AC=
;
(4)
若CD=8,BD=4,则AD=
.
(5)
若AB=5,AC=4,则CD=
.
4
6
16
2.4
随堂演练
5.(1)如图1,请你增加一个条件:∠
=
∠
(或∠
=∠
),使△ABC∽△ACD.
(2)如图2,请你增加一个条件:∠
=
∠
(或∠
=∠
),使
△ABC∽△AED.
ACB
ADC
ABC
ACD
ACB
ADE
ABC
AED
随堂演练
6.如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E,连接BD.
(1)请你找出图中所有的相似三角形;
(2)请选择其中的一对相似三角形予以证明.
解:(1)△DBE∽△DAB;△DBE∽△CAE;△ABD∽△AEC.
(2)选择△ABD∽△AEC.
∵DA是∠BAC的平分线,∴∠BAD=∠CAE.又∵∠D=∠C,∴△ABD∽△AEC.
(3)在上题条件下,若DE=3,EA=7,则BD=______.
随堂演练
证明:
∵
△ABC
的高AD、BE交于点F,
∴
∠FEA=∠FDB=90°,
∠AFE
=∠BFD
(对顶角相等).
∴
△FEA
∽
△
FDB,
∴
7.
如图,△ABC
的高
AD、BE
交于点
F.
求证:
D
C
A
B
E
F
随堂演练
证明:
∵∠BAC=
∠1+
∠DAC,
∠DAE=
∠3+
∠DAC,∠1=∠3,
∴
∠BAC=∠DAE.
∵
∠C=180°-∠2-∠DOC
,
∠E=180°-∠3-∠AOE,
∠DOC
=∠AOE(对顶角相等),
∴
∠C=
∠E.
∴
△ABC∽△ADE.
8.
如图,∠1=∠2=∠3,求证:△ABC
∽△ADE.
A
B
C
D
E
1
3
2
O
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
第二十七章
相似
第二节
相似三角形
第三课时
相似三角形的判定(3)
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
观察三角尺,其中同样角度(30°与60°)的两个三角尺大小不同,它们一定相似吗?
一定相似
第二部分
新课目标
新课目标
1.掌握相似三角形的判定定理:“如果一个三角
形的两个角与另一个三角形的两个角对应相
等,那么这两个三角形相似”.
2.了解“斜边的比等于一组直角边的比的两相直
角三角形相似”.
3.
会进行简单的证明、计算.
第三部分
新课进行时
新课进行时
核心知识点一
两角对应相等与三角形相似及其应用
作△ABC和△A'B'C',使得∠A=∠A'=55°,∠B=∠B'=85°,这时它们的第三个角满足∠C=∠C'吗?分别度量这两个三角形的边长,计算
,你有什么发现?
A
B
C
A'
B'
C'
满足:∠C
=
∠C'
△ABC∽△A'B'C'
证明:在
△ABC
的边
AB(或
AB
的延长线)上,截取
AD=A′B′,过点
D
作
DE
//
BC,交
AC
于点
E,则有△ADE
∽△ABC,∠ADE
=∠B.
∵∠B=∠B′,
∴∠ADE=∠B′.
又∵
AD=A′B′,∠A=∠A′,
∴△ADE
≌△A′B′C′,
∴△A′B′C′
∽△ABC.
C
A
A'
B
B'
C'
D
E
如何证明△A′B′C′∽△ABC?
新课进行时
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵
∠A=∠A',∠B=∠B',
∴
△ABC
∽
△A'B'C'.
C
A
B
A'
B'
C'
新课进行时
归纳
符号语言
证明:∵
在△
ABC中,∠A=40
°
,
∠B=80
°
,
∴
∠C=180
°-∠A-∠B=60
°.
∵
在△DEF中,∠E=80
°,
∠F=60
°.
∴
∠B=∠E,∠C=∠F.
∴
△ABC
∽△DEF.
例1
如图,△ABC
和
△DEF
中,∠A=40°,∠B=80°,∠E=80
°,∠F=60
°
.求证:△ABC
∽△DEF.
A
C
B
F
E
D
典例精析
新课进行时
对于两个直角三角形,我们还可以用
“HL”判定它们全等.
那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
思考
如图,在
Rt△ABC
和
Rt△A′B′C′
中,∠C=90°,
∠C′=90°,
.求证:Rt△ABC
∽
Rt△A′B′C′.
C
A
A'
B
B'
C'
要证明两个三角形相似,即是需要
证明什么呢?
新课进行时
核心知识点二
两个直角三角形的相似
证明:设____________=
k
,则AB=kA′B′,AC=kA′B′.
由
,得
∴
________.
∴
Rt
△ABC
∽
Rt
△A′B′C′.
勾股定理
∴
C
A
A'
B
B'
C'
新课进行时
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,
那么这两个直角三角形相似。
直角三角形相似的定理之HL
A
B
C
△ABC∽△A1B1C1
A1
B1
C1
在Rt△ABC
和
Rt△A1B1C1中
新课进行时
符号语言
例2
如图,Rt△ABC中∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长.
解:∵
ED⊥AB,∠C=90°,
∴∠EDA=∠C
又∠A=
∠A
∴△AED∽△ABC
D
A
B
C
E
思考:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.图中有哪几对相似三角形?为什么?
分析:∵CD⊥AB,∴∠CDB=90°.
∴∠B+∠BCD=90°.
又∵∠ACB=90°,∴∠B+∠A=90°.∴∠BCD=∠A
在△ABC和△CBD中,∵∠ACB=∠CDB=90°,∠BCD=∠A,∴△ABC∽△CBD.
请你再找出其他的几对相似三角形:
△ABC∽△ACD
△CBD∽△ACD
思考:1.根据以上结论,你发现了什么?
2.直角三角形相似的判定有哪些?
新课进行时
小组讨论:如何根据题目特点灵活选用本节所学相似三角形的判定方法?
证两三角形相似,若已具备一组角对应相等,则应先考虑“两角对应相等的两个三角形相似”这一判定方法,而找等角时常用到公共角、对顶角、等角(或同角)的余角相等等一些隐含条件.判定直角三角形相似时,可以用其相似独有的判定方法,也可以用一般三角形相似的判定方法.不过,更多的时候是用两角相等来证.
【反思小结】
新课进行时
第四部分
知识小结
知识小结
两角分别相等的两个三角形相似
利用两角判定三角形相似
直角三角形相似的判定
思想方法小结:
类比、转化的数学思想
第五部分
随堂演练
1.
在
Rt△ABC
和
Rt△A′B′C′
中,∠C=∠C′=90°,依据下列各组条件判定这两个三角形是否相似.
(1)
∠A=35°,∠B′=55°.
;
(2)
AC=3,BC=4,A′C′=6,B′C′=8.
;
(3)
AB=10,AC=8,A′B′=25,B′C′=15.
.
相似
相似
相似
随堂演练
2.下列结论:
①所有的等腰三角形都相似,
②有一个角是80°的两个等腰三角形相似,
③有一个角是100°的两个等腰三角形相似,
④有一个角相等的两个等腰三角形相似,其中
正确的有(
)
A.1个
B.2个
C.3个
D.4个
A
3.如图1,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3,则
的值为
( )
B
A.
B.
C.
D.
随堂演练
4.如图,在Rt△ABC中,
∠ACB=90°,CD是斜边AB上的高.
(1)
若AD=8,BD=2,则CD=
;
(2)
若BD=4,AB=9,则BC=
;
(3)
若AD=2,AB=3,则AC=
;
(4)
若CD=8,BD=4,则AD=
.
(5)
若AB=5,AC=4,则CD=
.
4
6
16
2.4
随堂演练
5.(1)如图1,请你增加一个条件:∠
=
∠
(或∠
=∠
),使△ABC∽△ACD.
(2)如图2,请你增加一个条件:∠
=
∠
(或∠
=∠
),使
△ABC∽△AED.
ACB
ADC
ABC
ACD
ACB
ADE
ABC
AED
随堂演练
6.如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E,连接BD.
(1)请你找出图中所有的相似三角形;
(2)请选择其中的一对相似三角形予以证明.
解:(1)△DBE∽△DAB;△DBE∽△CAE;△ABD∽△AEC.
(2)选择△ABD∽△AEC.
∵DA是∠BAC的平分线,∴∠BAD=∠CAE.又∵∠D=∠C,∴△ABD∽△AEC.
(3)在上题条件下,若DE=3,EA=7,则BD=______.
随堂演练
证明:
∵
△ABC
的高AD、BE交于点F,
∴
∠FEA=∠FDB=90°,
∠AFE
=∠BFD
(对顶角相等).
∴
△FEA
∽
△
FDB,
∴
7.
如图,△ABC
的高
AD、BE
交于点
F.
求证:
D
C
A
B
E
F
随堂演练
证明:
∵∠BAC=
∠1+
∠DAC,
∠DAE=
∠3+
∠DAC,∠1=∠3,
∴
∠BAC=∠DAE.
∵
∠C=180°-∠2-∠DOC
,
∠E=180°-∠3-∠AOE,
∠DOC
=∠AOE(对顶角相等),
∴
∠C=
∠E.
∴
△ABC∽△ADE.
8.
如图,∠1=∠2=∠3,求证:△ABC
∽△ADE.
A
B
C
D
E
1
3
2
O
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
