27.3 第2课时 位似(2) 课件(共31张PPT)
文档属性
| 名称 | 27.3 第2课时 位似(2) 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 17:36:31 | ||
图片预览







文档简介
(共31张PPT)
第二十七章
相似
第三节
位似
第二课时
位似(2)
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
在前面几册教科书中,我们学习了在平面直角坐标系中,如何用坐标表示某些平移、轴对称、旋转(中心对称)等变换,相似也是一种图形的变换,一些特殊的相似(如位似)也可以用图形坐标的变化来表示.
本节课就来学习这方面的知识.
第二部分
新课目标
新课目标
1.
理解平面直角坐标系中,位似图形对应点的坐标之间的联系.
2.
会用图形的坐标的变化表示图形的位似变换,掌握
把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
教学重(难)点:会用图形的坐标的变化表示图形的位似变换,掌握
把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
第三部分
新课进行时
新课进行时
核心知识点一
坐标系中的位似
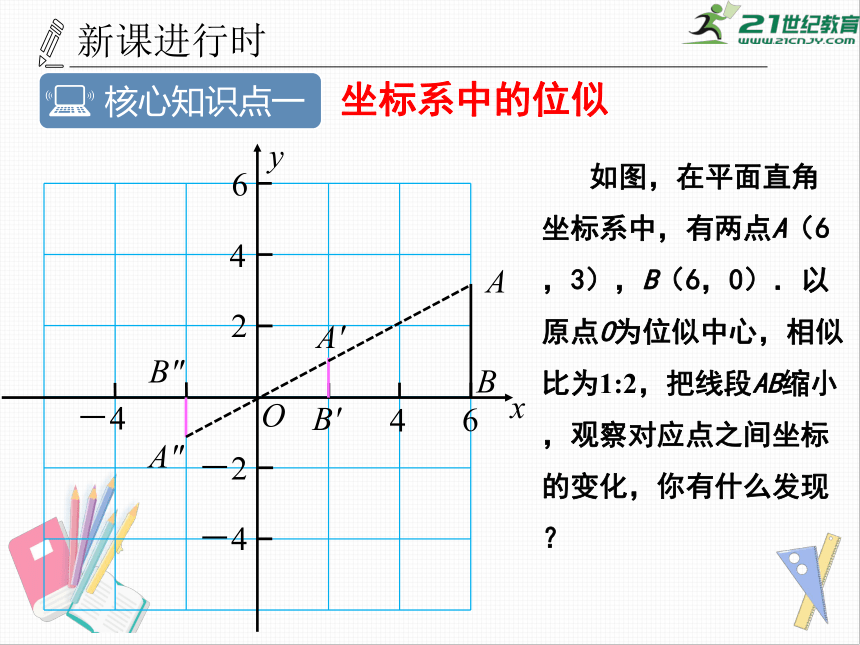
如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为1:2,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
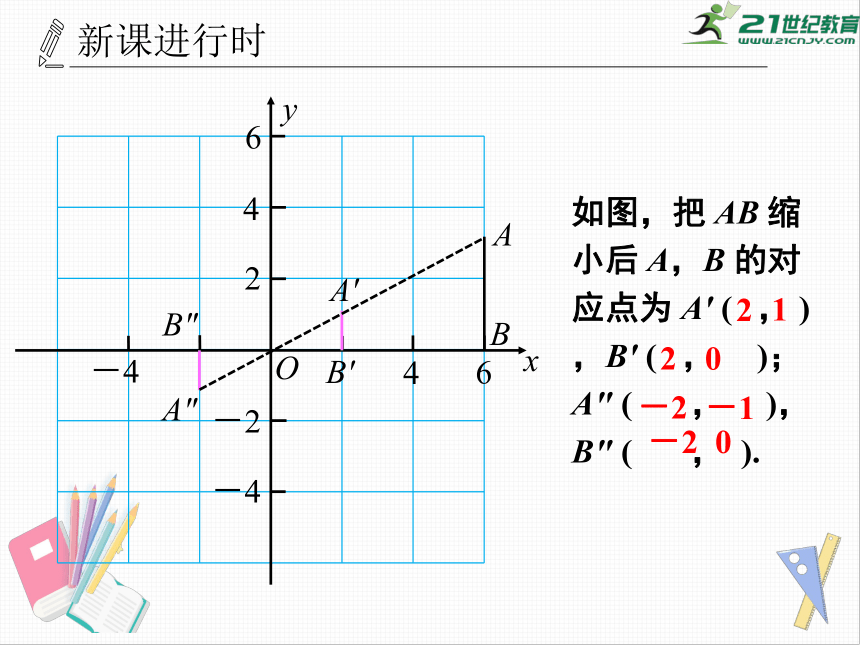
如图,把
AB
缩小后
A,B
的对应点为
A′
(
,
),B'
(
,
);
A"
(
,
),
B"
(
,
).
2
1
2
0
-2
-1
-2
0
新课进行时
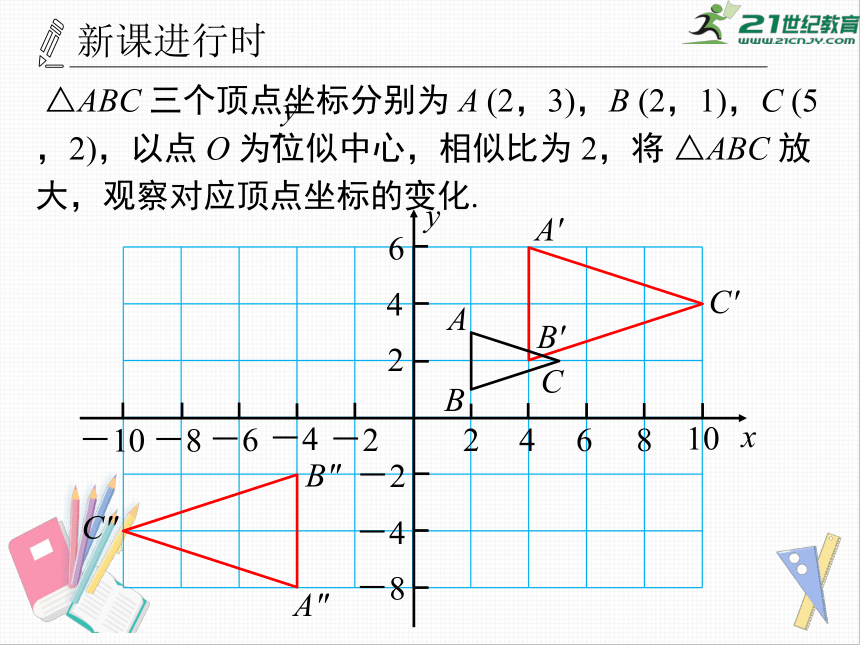
△ABC
三个顶点坐标分别为
A
(2,3),B
(2,1),C
(5,2),以点
O
为位似中心,相似比为
2,将
△ABC
放大,观察对应顶点坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
y
新课进行时
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
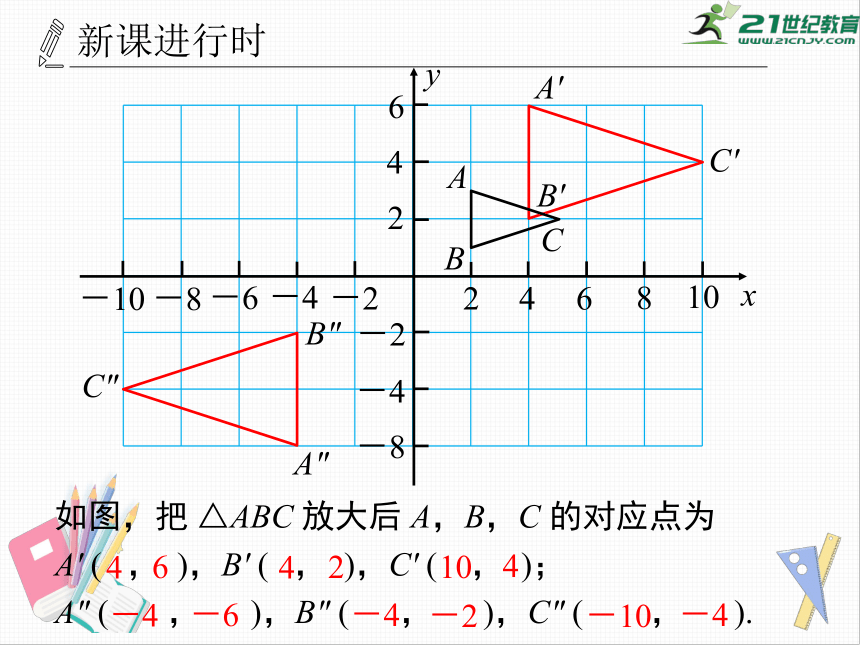
如图,把
△ABC
放大后
A,B,C
的对应点为
A'
(
,
),B'
(
,
),C'
(
,
);
A"
(
,
),B"
(
,
),C"
(
,
).
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
新课进行时
小组讨论:1.
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
2.
所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
【反思小结】
1.
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.
当位似图形在原点同侧时,其对应顶点的坐标的
比为
k;当位似图形在原点两侧时,其对应顶点的坐标的比为-k.
3.
当
k>1
时,图形扩大为原来的
k
倍;当
0<k<1时,图形缩小为原来的
k
倍.
新课进行时
例:如图,在平面直角坐标系中,△ABO
三个顶点的坐标分别为
A
(-2,4),B
(-2,0),O
(0,0).
以原点
O
为位似中心,画出一个三角形使它与
△ABO
的相似比为
3
:
2.
2
4
6
2
-2
-4
x
y
A
B
O
新课进行时
核心知识点二
平面直角坐标系中的位似作图
2
4
6
2
-2
-4
x
y
A
B
O
提示:画三角形关键
是确定它各顶点的坐
标.
根据前面的归纳
可知,点
A
的对应点
A′
的坐标为
,
即(-3,6),类似地,可以确定其他顶点的坐标.
解:利用位似中对应点的坐标的变化规律,分别取点
A′
(-3,6),B′
(-3,0),O
(0,0).
A′
B′
顺次连接点
A′
,B′
,O,所得的
△A′
B′
O
就是要画的一个图形.
还有其他画法吗?自己试一试.
新课进行时
小组讨论:在平面直角坐标系中,如何画一个图形关于原点位似的图形?
在平面直角坐标系中,画一个图形关于原点位似的图形的步骤:
1.根据平面直角坐标中,位似图形坐标之间的变化规律求出原图形各顶点的对应点的坐标;
2.在平面直角坐标系中描出各对应点;
3.顺次连接各对应点,所得图形即为所求.
【反思小结】
新课进行时
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在右图所示的图案中,你能找到这些变换吗?
新课进行时
第四部分
知识小结
知识小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
思想方法小结:
数形结合、分类讨论的数学思想
第五部分
随堂演练
1.将平面直角坐标系中某个图案的各点坐标作
如下变化,其中属于位似变换的是(
)
A.将各点的纵坐标乘以2,横坐标不变
B.将各点的横坐标除以2,纵坐标不变
C.将各点的横坐标、纵坐标都乘以2
D.将各点的纵坐标减去2,横坐标加上2
C
随堂演练
2.
如图,线段
AB
两个端点的坐标分别为
A
(4,4),B
(6,2),以原点
O
为位似中心,在第一象限内将线段
AB
缩小为原来的
1/2
后得到线段
CD,则端点
D
的坐标为
(
)
A.
(2,2)
B.
(2,1)
C.
(3,2)
D.
(3,1)
D
x
y
A
B
C
D
随堂演练
3.
已知△ABC三个顶点的坐标分别为(1,2),(-2
,3),(-1,0),把它们的横坐标和纵坐标分别
变成原来的2倍,得到点A′,B′,C′.下列说法
正确的是(
)
A.△A′B′C′与△ABC是位似图形,
位似中心是点(1,0)
B.△A′B′C′与△ABC是位似图形,
位似中心是点(0,0)
C.△A′B′C′与△ABC是相似图形,
但不是位似图形
D.△A′B′C′与△ABC不是相似图形
B
随堂演练
4.如图所示,某学习小组在讨论
“变化的鱼”
时,知道大鱼与小鱼是位似图形,则小鱼上
的点(a,b)对应大鱼上的点(
)
A.(-2a,-2b)
B.(-a,-2b)
C.(-2b,-2a)
D.(-2a,-b)
A
随堂演练
5.
在
13×13
的网格图中,已知
△ABC
和点
M
(1,2).
x
y
A
B
C
(1)
以点
M
为位似中心,位似比为
2,画出
△ABC的
位似图形
△A′B′C′;
M
A′
B′
C′
解:如图所示
(2)
写出
△A′B′C′
的各顶点坐标.
答:△A′B′C′
的各顶点坐标分别为
A′
(3,6),
B′
(5,2),
C′
(11,4).
随堂演练
6.
如图,点
A
的坐标为
(3,4),点
O
的坐标为
(0,0),点
B
的坐标为
(4,0).
4
x
y
A
B
4
3
(1)
将
△AOB
沿
x
轴向左平移1
个单位长度后得△A1O1B1,
则点
A1
的坐标为
,
△A1O1B1的面积为
;
(2,4)
8
(2)
将
△AOB
绕原点旋转
180°后得
△A2O2B2,
则点
A2
的坐标为
;
(-3,-4)
(3)
将
△AOB
沿
x
轴翻折后得
△A3O3B3,则点
A3
的
坐标为
;
(3,-4)
(4)
以
O
为位似中心,按比例尺
1
:
2
将
△AOB
放大后△A4O4B4,若点
B
在
x
轴负半轴上,则点
A
的坐标为
,△A4O4B4的面积为
.
(-6,-8)
32
随堂演练
O
C
解:画法一:将四边形
OABC
各顶点的坐标都乘
;在平
面直角坐标系中描点O
(0,
0),A'
(4,0),B'
(2,4),C′
(-2,2),用线段顺次连接O,A',B',C'.
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
C'
7.在平面直角坐标系中,四边形
OABC
的顶点坐标分别为
O
(0,0),A
(6,0),B
(3,6),C
(-3,3).
以原点
O
为位似中心,画出四边形
OABC
的位似图形,使它与四边形
OABC
的相似是
2
:
3.
随堂演练
画法二:将四边形
OABC
各顶点的坐
标都乘
;在平面
直角坐标系中描点
O
(0,0),A″
(-4,0),B″
(-2,-4),C″
(2,-2),用线段顺次连接O,A″,B″,C″.
O
C
2
4
6
4
6
B″
-2
-4
-4
x
y
A
B
A″
C″
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
第二十七章
相似
第三节
位似
第二课时
位似(2)
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
情景导学
在前面几册教科书中,我们学习了在平面直角坐标系中,如何用坐标表示某些平移、轴对称、旋转(中心对称)等变换,相似也是一种图形的变换,一些特殊的相似(如位似)也可以用图形坐标的变化来表示.
本节课就来学习这方面的知识.
第二部分
新课目标
新课目标
1.
理解平面直角坐标系中,位似图形对应点的坐标之间的联系.
2.
会用图形的坐标的变化表示图形的位似变换,掌握
把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
教学重(难)点:会用图形的坐标的变化表示图形的位似变换,掌握
把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
第三部分
新课进行时
新课进行时
核心知识点一
坐标系中的位似
如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为1:2,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
如图,把
AB
缩小后
A,B
的对应点为
A′
(
,
),B'
(
,
);
A"
(
,
),
B"
(
,
).
2
1
2
0
-2
-1
-2
0
新课进行时
△ABC
三个顶点坐标分别为
A
(2,3),B
(2,1),C
(5,2),以点
O
为位似中心,相似比为
2,将
△ABC
放大,观察对应顶点坐标的变化.
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
y
新课进行时
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
如图,把
△ABC
放大后
A,B,C
的对应点为
A'
(
,
),B'
(
,
),C'
(
,
);
A"
(
,
),B"
(
,
),C"
(
,
).
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
新课进行时
小组讨论:1.
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
2.
所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
【反思小结】
1.
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.
当位似图形在原点同侧时,其对应顶点的坐标的
比为
k;当位似图形在原点两侧时,其对应顶点的坐标的比为-k.
3.
当
k>1
时,图形扩大为原来的
k
倍;当
0<k<1时,图形缩小为原来的
k
倍.
新课进行时
例:如图,在平面直角坐标系中,△ABO
三个顶点的坐标分别为
A
(-2,4),B
(-2,0),O
(0,0).
以原点
O
为位似中心,画出一个三角形使它与
△ABO
的相似比为
3
:
2.
2
4
6
2
-2
-4
x
y
A
B
O
新课进行时
核心知识点二
平面直角坐标系中的位似作图
2
4
6
2
-2
-4
x
y
A
B
O
提示:画三角形关键
是确定它各顶点的坐
标.
根据前面的归纳
可知,点
A
的对应点
A′
的坐标为
,
即(-3,6),类似地,可以确定其他顶点的坐标.
解:利用位似中对应点的坐标的变化规律,分别取点
A′
(-3,6),B′
(-3,0),O
(0,0).
A′
B′
顺次连接点
A′
,B′
,O,所得的
△A′
B′
O
就是要画的一个图形.
还有其他画法吗?自己试一试.
新课进行时
小组讨论:在平面直角坐标系中,如何画一个图形关于原点位似的图形?
在平面直角坐标系中,画一个图形关于原点位似的图形的步骤:
1.根据平面直角坐标中,位似图形坐标之间的变化规律求出原图形各顶点的对应点的坐标;
2.在平面直角坐标系中描出各对应点;
3.顺次连接各对应点,所得图形即为所求.
【反思小结】
新课进行时
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在右图所示的图案中,你能找到这些变换吗?
新课进行时
第四部分
知识小结
知识小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
平面直角坐标系中的图形变换
坐标变化规律
平面直角坐标系中的位似图形的画法
思想方法小结:
数形结合、分类讨论的数学思想
第五部分
随堂演练
1.将平面直角坐标系中某个图案的各点坐标作
如下变化,其中属于位似变换的是(
)
A.将各点的纵坐标乘以2,横坐标不变
B.将各点的横坐标除以2,纵坐标不变
C.将各点的横坐标、纵坐标都乘以2
D.将各点的纵坐标减去2,横坐标加上2
C
随堂演练
2.
如图,线段
AB
两个端点的坐标分别为
A
(4,4),B
(6,2),以原点
O
为位似中心,在第一象限内将线段
AB
缩小为原来的
1/2
后得到线段
CD,则端点
D
的坐标为
(
)
A.
(2,2)
B.
(2,1)
C.
(3,2)
D.
(3,1)
D
x
y
A
B
C
D
随堂演练
3.
已知△ABC三个顶点的坐标分别为(1,2),(-2
,3),(-1,0),把它们的横坐标和纵坐标分别
变成原来的2倍,得到点A′,B′,C′.下列说法
正确的是(
)
A.△A′B′C′与△ABC是位似图形,
位似中心是点(1,0)
B.△A′B′C′与△ABC是位似图形,
位似中心是点(0,0)
C.△A′B′C′与△ABC是相似图形,
但不是位似图形
D.△A′B′C′与△ABC不是相似图形
B
随堂演练
4.如图所示,某学习小组在讨论
“变化的鱼”
时,知道大鱼与小鱼是位似图形,则小鱼上
的点(a,b)对应大鱼上的点(
)
A.(-2a,-2b)
B.(-a,-2b)
C.(-2b,-2a)
D.(-2a,-b)
A
随堂演练
5.
在
13×13
的网格图中,已知
△ABC
和点
M
(1,2).
x
y
A
B
C
(1)
以点
M
为位似中心,位似比为
2,画出
△ABC的
位似图形
△A′B′C′;
M
A′
B′
C′
解:如图所示
(2)
写出
△A′B′C′
的各顶点坐标.
答:△A′B′C′
的各顶点坐标分别为
A′
(3,6),
B′
(5,2),
C′
(11,4).
随堂演练
6.
如图,点
A
的坐标为
(3,4),点
O
的坐标为
(0,0),点
B
的坐标为
(4,0).
4
x
y
A
B
4
3
(1)
将
△AOB
沿
x
轴向左平移1
个单位长度后得△A1O1B1,
则点
A1
的坐标为
,
△A1O1B1的面积为
;
(2,4)
8
(2)
将
△AOB
绕原点旋转
180°后得
△A2O2B2,
则点
A2
的坐标为
;
(-3,-4)
(3)
将
△AOB
沿
x
轴翻折后得
△A3O3B3,则点
A3
的
坐标为
;
(3,-4)
(4)
以
O
为位似中心,按比例尺
1
:
2
将
△AOB
放大后△A4O4B4,若点
B
在
x
轴负半轴上,则点
A
的坐标为
,△A4O4B4的面积为
.
(-6,-8)
32
随堂演练
O
C
解:画法一:将四边形
OABC
各顶点的坐标都乘
;在平
面直角坐标系中描点O
(0,
0),A'
(4,0),B'
(2,4),C′
(-2,2),用线段顺次连接O,A',B',C'.
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
C'
7.在平面直角坐标系中,四边形
OABC
的顶点坐标分别为
O
(0,0),A
(6,0),B
(3,6),C
(-3,3).
以原点
O
为位似中心,画出四边形
OABC
的位似图形,使它与四边形
OABC
的相似是
2
:
3.
随堂演练
画法二:将四边形
OABC
各顶点的坐
标都乘
;在平面
直角坐标系中描点
O
(0,0),A″
(-4,0),B″
(-2,-4),C″
(2,-2),用线段顺次连接O,A″,B″,C″.
O
C
2
4
6
4
6
B″
-2
-4
-4
x
y
A
B
A″
C″
随堂演练
第六部分
课后作业
课后作业
文本
文本
文本
单击此处添加文本
文本
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
