4.3.2 角的比较与运算 同步练习(含答案)
文档属性
| 名称 | 4.3.2 角的比较与运算 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 961.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 20:01:22 | ||
图片预览




文档简介
人教版数学(七上)第4章 4.3.2 角的比较与运算
同步练习
一、选择题
1. 将∠1,∠2的顶点和其中一边重合,另一边都落在重合边的同侧,且∠1>
∠2,那么∠1的另一边落在∠2的( )
A.另一边上 B.内部
C.外部 D.无法判断
2. 如图,AM为∠BAC的平分线,下列等式错误的是( )
A.∠BAC=∠BAM B.∠BAM=∠CAM
C.∠BAM=2∠CAM D.2∠CAM=∠BAC
3. 22°20′×8等于( )
A.178°20′ B.178°40′
C.176°16′ D.178°30′
4. 如图,射线OB,OC将∠AOD分成三部分,下列判断不一定成立的是( )
A.如果∠AOB=∠COD,那么∠AOC=∠BOD
B.如果∠AOB>∠COD,那么∠AOC>∠BOD
C.如果∠AOB<∠COD,那么∠AOC<∠BOD
D.如果∠AOB=∠BOC,那么∠AOC=∠BOD
5. 如图所示,已知O是直线AB上一点,∠1=68°,OD平分∠BOC,则∠2的度数是( )
A.40° B.45° C.44° D.46°
6. 已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为( )
A.28° B.112° C.28°或112° D.68°
7. 用度、分、秒表示30.26°正确的是( )
A.30°26′ B.30°36′15″
C.30°15′36″ D.30°20′6″
8. 把15°48′36″化成以度为单位是( )
A.15.8° B.15.483 6° C.15.81° D.15.36°
9. 如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,下列
结论:①∠EOD=90°;②∠COE=∠AOD;③∠COE=∠DOB;
④∠COE+∠BOD=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
10. 计算:
(1)180°-46°42′=____;
(2)28°36′+72°24′=___;
(3)50°24′×3=____;
(4)49°28′52″÷4=____.
11. 如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为____.
12. 已知两个角的和是67°56′,差是12°40′,则这两个角的度数分别是_ _, _.
如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线,则
∠DOE=___.
14. 如图,CD是直线,∠ABD=90°,BE是∠ABD的平分线,则∠CBE的度数为____.
三、解答题
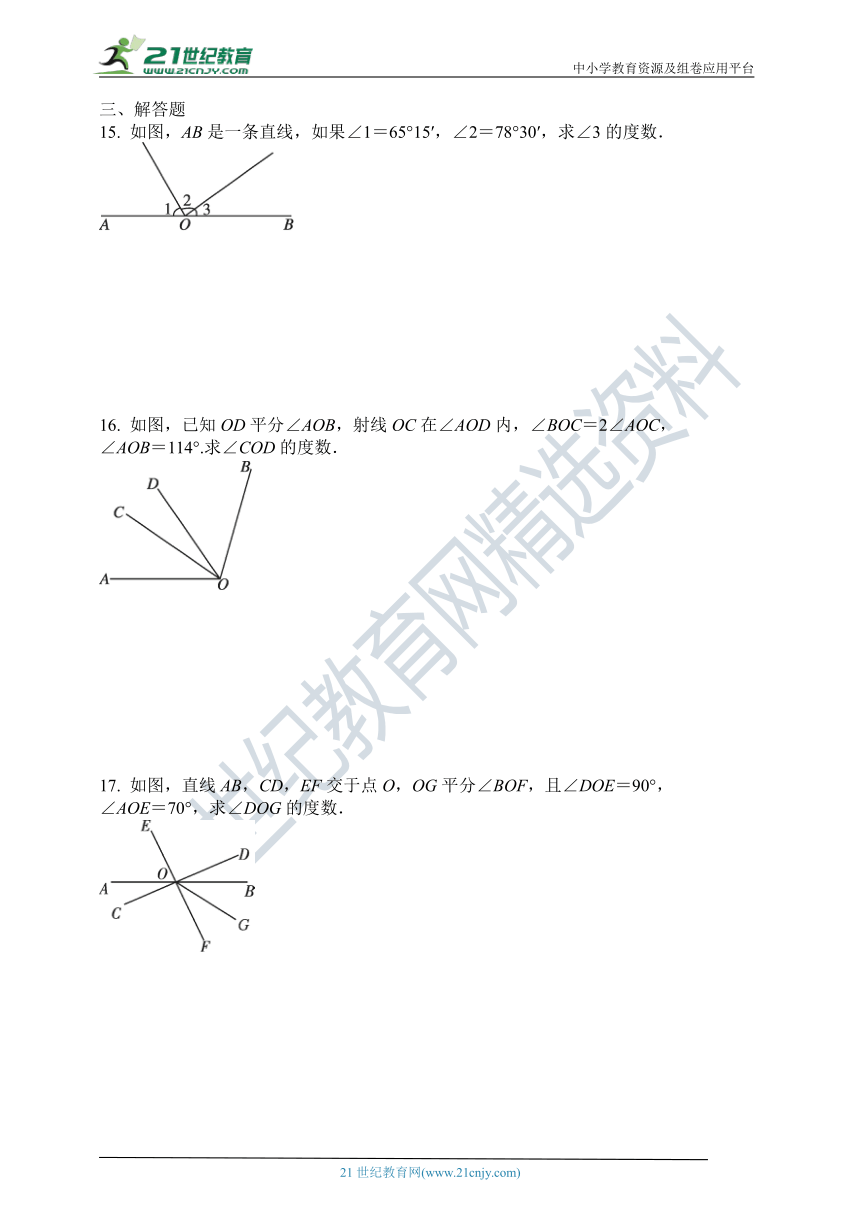
15. 如图,AB是一条直线,如果∠1=65°15′,∠2=78°30′,求∠3的度数.
16. 如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,
∠AOB=114°.求∠COD的度数.
17. 如图,直线AB,CD,EF交于点O,OG平分∠BOF,且∠DOE=90°,
∠AOE=70°,求∠DOG的度数.
18. 如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
(1)若∠COE=∠AOE,求∠AOC的度数;
(2)若∠BOC-∠AOC=72°,求∠BOC的度数.
参考答案
一、选择题
1. 将∠1,∠2的顶点和其中一边重合,另一边都落在重合边的同侧,且∠1>
∠2,那么∠1的另一边落在∠2的( )
A.另一边上 B.内部
C.外部 D.无法判断
【答案】C
2. 如图,AM为∠BAC的平分线,下列等式错误的是( )
A.∠BAC=∠BAM B.∠BAM=∠CAM
C.∠BAM=2∠CAM D.2∠CAM=∠BAC
【答案】C
3. 22°20′×8等于( )
A.178°20′ B.178°40′
C.176°16′ D.178°30′
【答案】B
4. 如图,射线OB,OC将∠AOD分成三部分,下列判断不一定成立的是( )
A.如果∠AOB=∠COD,那么∠AOC=∠BOD
B.如果∠AOB>∠COD,那么∠AOC>∠BOD
C.如果∠AOB<∠COD,那么∠AOC<∠BOD
D.如果∠AOB=∠BOC,那么∠AOC=∠BOD
【答案】D
5. 如图所示,已知O是直线AB上一点,∠1=68°,OD平分∠BOC,则∠2的度数是( )
A.40° B.45° C.44° D.46°
【答案】C
【解析】 ∵OD平分∠BOC,∴∠BOC=2∠1=2×68°=136°,
∴∠2=180°-∠BOC=180°-136°=44°.
6. 已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为( )
A.28° B.112° C.28°或112° D.68°
【答案】C
【解析】 如答图所示,当OC在∠AOB内部时,
∠BOC=∠AOB-∠AOC=70°-42°=28°;
当OC在∠AOB外部时,∠BOC=∠AOB+∠AOC=70°+42°=112°.故选C.
7. 用度、分、秒表示30.26°正确的是( )
A.30°26′ B.30°36′15″
C.30°15′36″ D.30°20′6″
【答案】C
【解析】 0.26°=60′×0.26=15.6′,0.6′=60″×0.6=36″,∴30.26°=30°15′36″.
故选C.
8. 把15°48′36″化成以度为单位是( )
A.15.8° B.15.483 6° C.15.81° D.15.36°
【答案】C
【解析】 15°48′36″=15°+48′+(36÷60)′=15°+(48.6÷60)°=15.81°.故选C.
9. 如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,下列
结论:①∠EOD=90°;②∠COE=∠AOD;③∠COE=∠DOB;
④∠COE+∠BOD=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
【答案】C
二、填空题
10. 计算:
(1)180°-46°42′=____;
(2)28°36′+72°24′=___;
(3)50°24′×3=____;
(4)49°28′52″÷4=____.
【答案】(1)180°-46°42′=__133°18′__;
(2)28°36′+72°24′=__101°__;
(3)50°24′×3=__151°12′__;
(4)49°28′52″÷4=__12°22′13″__.
11. 如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为____.
【答案】150°42′
【解析】 ∵∠BOC+∠AOC=180°,∠BOC=29°18′,
∴∠AOC=180°-29°18′=150°42′.
12. 已知两个角的和是67°56′,差是12°40′,则这两个角的度数分别是_ _, _.
【答案】40°18′,27°38′
【解析】 设一个角的度数为x,则另一个角的度数为67°56′-x,
依题意得x-(67°56′-x)=12°40′,解得x=40°18′,∴67°56′-x=27°38′,
则这两个角分别是40°18′,27°38′.
13. 如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线,则
∠DOE=___.
【答案】90°
【解析】 ∵OD是∠AOC的平分线,∴∠COD=∠AOC,
∵OE是∠COB的平分线,∴∠COE=∠COB.
∴∠DOE=∠COD+∠COE=∠AOC+∠COB=∠AOB,
∵∠AOB=180°,∴∠DOE=90°.
14. 如图,CD是直线,∠ABD=90°,BE是∠ABD的平分线,则∠CBE的度数为____.
【答案】135°
【解析】 ∵BE是∠ABD的平分线,∴∠DBE=∠ABD=×90°=45°,
∴∠CBE=∠CBD-∠DBE=180°-45°=135°.
三、解答题
15. 如图,AB是一条直线,如果∠1=65°15′,∠2=78°30′,求∠3的度数.
【答案】解:∠3=180°-∠1-∠2=180°-65°15′-78°30′=36°15′.
16. 如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°.求∠COD的度数.
【答案】解:∵OD平分∠AOB,∠AOB=114°,
∴∠AOD=∠BOD=∠AOB=57°.
∵∠BOC=2∠AOC,∴∠AOC=∠AOB=38°.
∴∠COD=∠AOD-∠AOC=57°-38°=19°.
17. 如图,直线AB,CD,EF交于点O,OG平分∠BOF,且∠DOE=90°,∠AOE=70°,求∠DOG的度数.
【答案】解:∵∠AOE=70°,
又∵∠BOF+∠BOE=180°,∠AOE+∠BOE=180°,∴∠BOF=∠AOE=70°,
又∵OG平分∠BOF,∴∠GOF=∠BOF=35°,
又∵∠DOE=90°,
∴∠DOG=180°-∠GOF-∠DOE=55°.
18. 如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
(1)若∠COE=∠AOE,求∠AOC的度数;
(2)若∠BOC-∠AOC=72°,求∠BOC的度数.
【答案】解:(1)∵∠COE=∠AOE,∴∠AOE=3∠COE,
∵OE是∠AOB的平分线,∴∠AOB=2∠AOE=6∠COE,
∵∠AOB=108°,∴∠COE=18°,∴∠AOC=2∠COE=2×18°=36°;
(2)设∠BOC=x,则∠AOC=108°-x,
∵∠BOC-∠AOC=72°,∴x-(108°-x)=72°,
解得x=90°,即∠BOC=90°.
同步练习
一、选择题
1. 将∠1,∠2的顶点和其中一边重合,另一边都落在重合边的同侧,且∠1>
∠2,那么∠1的另一边落在∠2的( )
A.另一边上 B.内部
C.外部 D.无法判断
2. 如图,AM为∠BAC的平分线,下列等式错误的是( )
A.∠BAC=∠BAM B.∠BAM=∠CAM
C.∠BAM=2∠CAM D.2∠CAM=∠BAC
3. 22°20′×8等于( )
A.178°20′ B.178°40′
C.176°16′ D.178°30′
4. 如图,射线OB,OC将∠AOD分成三部分,下列判断不一定成立的是( )
A.如果∠AOB=∠COD,那么∠AOC=∠BOD
B.如果∠AOB>∠COD,那么∠AOC>∠BOD
C.如果∠AOB<∠COD,那么∠AOC<∠BOD
D.如果∠AOB=∠BOC,那么∠AOC=∠BOD
5. 如图所示,已知O是直线AB上一点,∠1=68°,OD平分∠BOC,则∠2的度数是( )
A.40° B.45° C.44° D.46°
6. 已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为( )
A.28° B.112° C.28°或112° D.68°
7. 用度、分、秒表示30.26°正确的是( )
A.30°26′ B.30°36′15″
C.30°15′36″ D.30°20′6″
8. 把15°48′36″化成以度为单位是( )
A.15.8° B.15.483 6° C.15.81° D.15.36°
9. 如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,下列
结论:①∠EOD=90°;②∠COE=∠AOD;③∠COE=∠DOB;
④∠COE+∠BOD=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
10. 计算:
(1)180°-46°42′=____;
(2)28°36′+72°24′=___;
(3)50°24′×3=____;
(4)49°28′52″÷4=____.
11. 如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为____.
12. 已知两个角的和是67°56′,差是12°40′,则这两个角的度数分别是_ _, _.
如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线,则
∠DOE=___.
14. 如图,CD是直线,∠ABD=90°,BE是∠ABD的平分线,则∠CBE的度数为____.
三、解答题
15. 如图,AB是一条直线,如果∠1=65°15′,∠2=78°30′,求∠3的度数.
16. 如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,
∠AOB=114°.求∠COD的度数.
17. 如图,直线AB,CD,EF交于点O,OG平分∠BOF,且∠DOE=90°,
∠AOE=70°,求∠DOG的度数.
18. 如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
(1)若∠COE=∠AOE,求∠AOC的度数;
(2)若∠BOC-∠AOC=72°,求∠BOC的度数.
参考答案
一、选择题
1. 将∠1,∠2的顶点和其中一边重合,另一边都落在重合边的同侧,且∠1>
∠2,那么∠1的另一边落在∠2的( )
A.另一边上 B.内部
C.外部 D.无法判断
【答案】C
2. 如图,AM为∠BAC的平分线,下列等式错误的是( )
A.∠BAC=∠BAM B.∠BAM=∠CAM
C.∠BAM=2∠CAM D.2∠CAM=∠BAC
【答案】C
3. 22°20′×8等于( )
A.178°20′ B.178°40′
C.176°16′ D.178°30′
【答案】B
4. 如图,射线OB,OC将∠AOD分成三部分,下列判断不一定成立的是( )
A.如果∠AOB=∠COD,那么∠AOC=∠BOD
B.如果∠AOB>∠COD,那么∠AOC>∠BOD
C.如果∠AOB<∠COD,那么∠AOC<∠BOD
D.如果∠AOB=∠BOC,那么∠AOC=∠BOD
【答案】D
5. 如图所示,已知O是直线AB上一点,∠1=68°,OD平分∠BOC,则∠2的度数是( )
A.40° B.45° C.44° D.46°
【答案】C
【解析】 ∵OD平分∠BOC,∴∠BOC=2∠1=2×68°=136°,
∴∠2=180°-∠BOC=180°-136°=44°.
6. 已知∠AOB=70°,以O为端点作射线OC,使∠AOC=42°,则∠BOC的度数为( )
A.28° B.112° C.28°或112° D.68°
【答案】C
【解析】 如答图所示,当OC在∠AOB内部时,
∠BOC=∠AOB-∠AOC=70°-42°=28°;
当OC在∠AOB外部时,∠BOC=∠AOB+∠AOC=70°+42°=112°.故选C.
7. 用度、分、秒表示30.26°正确的是( )
A.30°26′ B.30°36′15″
C.30°15′36″ D.30°20′6″
【答案】C
【解析】 0.26°=60′×0.26=15.6′,0.6′=60″×0.6=36″,∴30.26°=30°15′36″.
故选C.
8. 把15°48′36″化成以度为单位是( )
A.15.8° B.15.483 6° C.15.81° D.15.36°
【答案】C
【解析】 15°48′36″=15°+48′+(36÷60)′=15°+(48.6÷60)°=15.81°.故选C.
9. 如图,点C,O,B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,下列
结论:①∠EOD=90°;②∠COE=∠AOD;③∠COE=∠DOB;
④∠COE+∠BOD=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
【答案】C
二、填空题
10. 计算:
(1)180°-46°42′=____;
(2)28°36′+72°24′=___;
(3)50°24′×3=____;
(4)49°28′52″÷4=____.
【答案】(1)180°-46°42′=__133°18′__;
(2)28°36′+72°24′=__101°__;
(3)50°24′×3=__151°12′__;
(4)49°28′52″÷4=__12°22′13″__.
11. 如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为____.
【答案】150°42′
【解析】 ∵∠BOC+∠AOC=180°,∠BOC=29°18′,
∴∠AOC=180°-29°18′=150°42′.
12. 已知两个角的和是67°56′,差是12°40′,则这两个角的度数分别是_ _, _.
【答案】40°18′,27°38′
【解析】 设一个角的度数为x,则另一个角的度数为67°56′-x,
依题意得x-(67°56′-x)=12°40′,解得x=40°18′,∴67°56′-x=27°38′,
则这两个角分别是40°18′,27°38′.
13. 如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线,则
∠DOE=___.
【答案】90°
【解析】 ∵OD是∠AOC的平分线,∴∠COD=∠AOC,
∵OE是∠COB的平分线,∴∠COE=∠COB.
∴∠DOE=∠COD+∠COE=∠AOC+∠COB=∠AOB,
∵∠AOB=180°,∴∠DOE=90°.
14. 如图,CD是直线,∠ABD=90°,BE是∠ABD的平分线,则∠CBE的度数为____.
【答案】135°
【解析】 ∵BE是∠ABD的平分线,∴∠DBE=∠ABD=×90°=45°,
∴∠CBE=∠CBD-∠DBE=180°-45°=135°.
三、解答题
15. 如图,AB是一条直线,如果∠1=65°15′,∠2=78°30′,求∠3的度数.
【答案】解:∠3=180°-∠1-∠2=180°-65°15′-78°30′=36°15′.
16. 如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°.求∠COD的度数.
【答案】解:∵OD平分∠AOB,∠AOB=114°,
∴∠AOD=∠BOD=∠AOB=57°.
∵∠BOC=2∠AOC,∴∠AOC=∠AOB=38°.
∴∠COD=∠AOD-∠AOC=57°-38°=19°.
17. 如图,直线AB,CD,EF交于点O,OG平分∠BOF,且∠DOE=90°,∠AOE=70°,求∠DOG的度数.
【答案】解:∵∠AOE=70°,
又∵∠BOF+∠BOE=180°,∠AOE+∠BOE=180°,∴∠BOF=∠AOE=70°,
又∵OG平分∠BOF,∴∠GOF=∠BOF=35°,
又∵∠DOE=90°,
∴∠DOG=180°-∠GOF-∠DOE=55°.
18. 如图,已知∠AOB=108°,OE是∠AOB的平分线,OC在∠AOE内.
(1)若∠COE=∠AOE,求∠AOC的度数;
(2)若∠BOC-∠AOC=72°,求∠BOC的度数.
【答案】解:(1)∵∠COE=∠AOE,∴∠AOE=3∠COE,
∵OE是∠AOB的平分线,∴∠AOB=2∠AOE=6∠COE,
∵∠AOB=108°,∴∠COE=18°,∴∠AOC=2∠COE=2×18°=36°;
(2)设∠BOC=x,则∠AOC=108°-x,
∵∠BOC-∠AOC=72°,∴x-(108°-x)=72°,
解得x=90°,即∠BOC=90°.
