4.3.3 余角和补角 同步练习(含答案)
文档属性
| 名称 | 4.3.3 余角和补角 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1004.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 09:36:11 | ||
图片预览



文档简介
人教版数学(七上)第4章 4.3.3 余角和补角
同步练习
一、选择题
1. 若一个角为65°,则它的补角的度数为( )
A.25° B.36° C.115° D.125°
2.若一个角为75°,则它的余角的度数为( )
A.285° B.105° C.75° D.15°
3. 下列说法正确的是( )
A.90°角是余角
B.如果一个角有补角,那么它一定有余角
C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补
D.66°角的余角是24°
4. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
5. 如图,下列说法中不正确的是( )
A.射线OA表示北偏东25° B.射线OB表示西北方向
C.射线OC表示西偏南80° D.射线OD表示南偏东70°
6. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA夹角为90°,则OB的方位角是( )
A.北偏西30° B.北偏西60°
C.东偏北30° D.东偏北60°
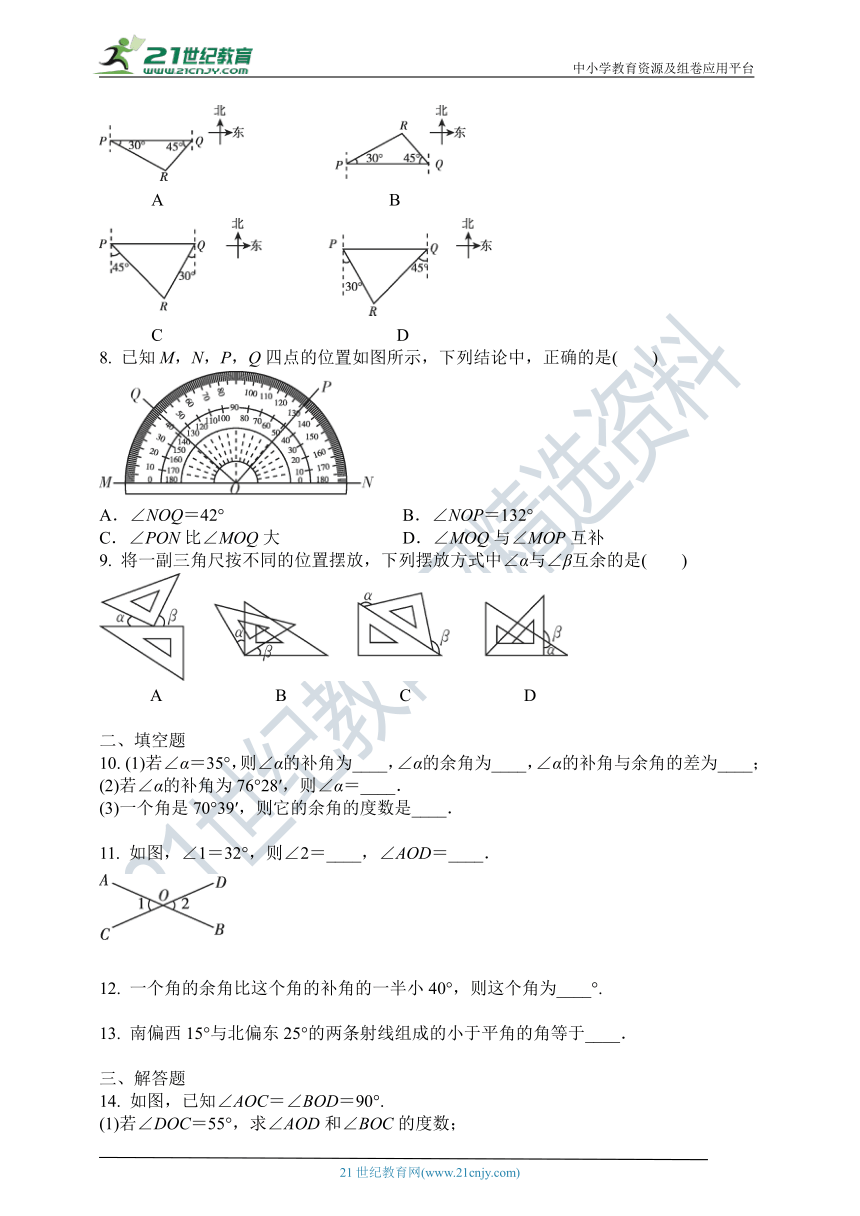
7. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,以下符合条件的示意图是( )
A B
C D
8. 已知M,N,P,Q四点的位置如图所示,下列结论中,正确的是( )
A.∠NOQ=42° B.∠NOP=132°
C.∠PON比∠MOQ大 D.∠MOQ与∠MOP互补
9. 将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )
A B C D
二、填空题
10. (1)若∠α=35°,则∠α的补角为____,∠α的余角为____,∠α的补角与余角的差为____;
(2)若∠α的补角为76°28′,则∠α=____.
(3)一个角是70°39′,则它的余角的度数是____.
11. 如图,∠1=32°,则∠2=____,∠AOD=____.
12. 一个角的余角比这个角的补角的一半小40°,则这个角为____°.
13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____.
三、解答题
14. 如图,已知∠AOC=∠BOD=90°.
(1)若∠DOC=55°,求∠AOD和∠BOC的度数;
(2)试说明:∠AOD=∠BOC.
15. 如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
16. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.
参考答案
一、选择题
1. 若一个角为65°,则它的补角的度数为( )
A.25° B.36° C.115° D.125°
【答案】C
2.若一个角为75°,则它的余角的度数为( )
A.285° B.105° C.75° D.15°
【答案】D
3. 下列说法正确的是( )
A.90°角是余角
B.如果一个角有补角,那么它一定有余角
C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补
D.66°角的余角是24°
【答案】D
4. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
【答案】C
5. 如图,下列说法中不正确的是( )
A.射线OA表示北偏东25° B.射线OB表示西北方向
C.射线OC表示西偏南80° D.射线OD表示南偏东70°
【答案】C
6. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA夹角为90°,则OB的方位角是( )
A.北偏西30° B.北偏西60°
C.东偏北30° D.东偏北60°
【答案】B
7. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,以下符合条件的示意图是( )
A B
C D
【答案】D
8. 已知M,N,P,Q四点的位置如图所示,下列结论中,正确的是( )
A.∠NOQ=42° B.∠NOP=132°
C.∠PON比∠MOQ大 D.∠MOQ与∠MOP互补
【答案】C
【解析】 如图所示:∠NOQ=138°,故选项A错误;
∠NOP=48°,故选项B错误;
∠PON=48°,∠MOQ=42°,故∠PON比∠MOQ大,故选项C正确;
∵∠MOQ=42°,∠MOP=132°,∠MOQ+∠MOP≠180°,∴∠MOQ与∠MOP不互补,选项D错误.故选C.
9. 将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )
A B C D
【答案】A
【解析】 A中∠α与∠β互余,B中∠α=∠β,C中∠α=∠β,D中∠α与∠β互补.故选A.
二、填空题
10. (1)若∠α=35°,则∠α的补角为____,∠α的余角为____,∠α的补角与余角的差为____;
(2)若∠α的补角为76°28′,则∠α=____.
(3)一个角是70°39′,则它的余角的度数是____.
【答案】(1) 145°; 55°; 90°(2) 103°32′;(3) 19°21′
11. 如图,∠1=32°,则∠2=____,∠AOD=____.
【答案】32°; 148°
12. 一个角的余角比这个角的补角的一半小40°,则这个角为____°.
【答案】80
【解析】 设这个角为x,则它的余角为(90°-x),补角为(180°-x).根据题意,得(180°-x)-(90°-x)=40°,解得x=80°.
13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____.
【答案】170°
【解析】 依题意画图如答图,则90°+15°+90°-25°=170°.
三、解答题
14. 如图,已知∠AOC=∠BOD=90°.
(1)若∠DOC=55°,求∠AOD和∠BOC的度数;
(2)试说明:∠AOD=∠BOC.
【答案】解:(1)∵∠AOC=∠BOD=90°,∠DOC=55°,
∴∠AOD=∠AOC-∠DOC=90°-55°=35°,
∠BOC=∠BOD-∠DOC=90°-55°=35°;
(2)∵∠AOD+∠DOC=90°,∠BOC+∠DOC=90°,
∴∠AOD=∠BOC(同角的余角相等).
15. 如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
【答案】解:(1)∵直线AB,CD相交于点O,
∴∠AOC和∠BOD与∠AOD互补.
∵OF平分∠AOE,∴∠AOF=∠EOF,
∵∠DOF=90°,∴∠COF=90°,则∠DOE=∠AOC(等角的余角相等),
∴∠DOE也是∠AOD的补角.
综上,与∠AOD互补的角有∠AOC,∠BOD,∠DOE;
(2)由(1)知∠AOC=∠BOD=∠DOE,
又∵∠AOC+∠AOE+∠DOE=180°,∴∠BOD=∠AOC==30°.
16. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.
【答案】解:(1)∵OE平分∠BOC,∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
故答案为∠BOE、∠COE;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=30°,∠COE=∠BOE=∠BOC,
∴∠AOC=2×30°=60°,∴∠BOC=180°﹣60°=120°,∴∠COE=∠BOC=60°,
∴∠DOE=∠COD+∠COE=90°;
(3)当∠AOD=α°时,∠DOE=90°.
同步练习
一、选择题
1. 若一个角为65°,则它的补角的度数为( )
A.25° B.36° C.115° D.125°
2.若一个角为75°,则它的余角的度数为( )
A.285° B.105° C.75° D.15°
3. 下列说法正确的是( )
A.90°角是余角
B.如果一个角有补角,那么它一定有余角
C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补
D.66°角的余角是24°
4. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
5. 如图,下列说法中不正确的是( )
A.射线OA表示北偏东25° B.射线OB表示西北方向
C.射线OC表示西偏南80° D.射线OD表示南偏东70°
6. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA夹角为90°,则OB的方位角是( )
A.北偏西30° B.北偏西60°
C.东偏北30° D.东偏北60°
7. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,以下符合条件的示意图是( )
A B
C D
8. 已知M,N,P,Q四点的位置如图所示,下列结论中,正确的是( )
A.∠NOQ=42° B.∠NOP=132°
C.∠PON比∠MOQ大 D.∠MOQ与∠MOP互补
9. 将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )
A B C D
二、填空题
10. (1)若∠α=35°,则∠α的补角为____,∠α的余角为____,∠α的补角与余角的差为____;
(2)若∠α的补角为76°28′,则∠α=____.
(3)一个角是70°39′,则它的余角的度数是____.
11. 如图,∠1=32°,则∠2=____,∠AOD=____.
12. 一个角的余角比这个角的补角的一半小40°,则这个角为____°.
13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____.
三、解答题
14. 如图,已知∠AOC=∠BOD=90°.
(1)若∠DOC=55°,求∠AOD和∠BOC的度数;
(2)试说明:∠AOD=∠BOC.
15. 如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
16. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.
参考答案
一、选择题
1. 若一个角为65°,则它的补角的度数为( )
A.25° B.36° C.115° D.125°
【答案】C
2.若一个角为75°,则它的余角的度数为( )
A.285° B.105° C.75° D.15°
【答案】D
3. 下列说法正确的是( )
A.90°角是余角
B.如果一个角有补角,那么它一定有余角
C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补
D.66°角的余角是24°
【答案】D
4. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等 B.等角的余角相等
C.同角的补角相等 D.等角的补角相等
【答案】C
5. 如图,下列说法中不正确的是( )
A.射线OA表示北偏东25° B.射线OB表示西北方向
C.射线OC表示西偏南80° D.射线OD表示南偏东70°
【答案】C
6. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA夹角为90°,则OB的方位角是( )
A.北偏西30° B.北偏西60°
C.东偏北30° D.东偏北60°
【答案】B
7. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,以下符合条件的示意图是( )
A B
C D
【答案】D
8. 已知M,N,P,Q四点的位置如图所示,下列结论中,正确的是( )
A.∠NOQ=42° B.∠NOP=132°
C.∠PON比∠MOQ大 D.∠MOQ与∠MOP互补
【答案】C
【解析】 如图所示:∠NOQ=138°,故选项A错误;
∠NOP=48°,故选项B错误;
∠PON=48°,∠MOQ=42°,故∠PON比∠MOQ大,故选项C正确;
∵∠MOQ=42°,∠MOP=132°,∠MOQ+∠MOP≠180°,∴∠MOQ与∠MOP不互补,选项D错误.故选C.
9. 将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )
A B C D
【答案】A
【解析】 A中∠α与∠β互余,B中∠α=∠β,C中∠α=∠β,D中∠α与∠β互补.故选A.
二、填空题
10. (1)若∠α=35°,则∠α的补角为____,∠α的余角为____,∠α的补角与余角的差为____;
(2)若∠α的补角为76°28′,则∠α=____.
(3)一个角是70°39′,则它的余角的度数是____.
【答案】(1) 145°; 55°; 90°(2) 103°32′;(3) 19°21′
11. 如图,∠1=32°,则∠2=____,∠AOD=____.
【答案】32°; 148°
12. 一个角的余角比这个角的补角的一半小40°,则这个角为____°.
【答案】80
【解析】 设这个角为x,则它的余角为(90°-x),补角为(180°-x).根据题意,得(180°-x)-(90°-x)=40°,解得x=80°.
13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____.
【答案】170°
【解析】 依题意画图如答图,则90°+15°+90°-25°=170°.
三、解答题
14. 如图,已知∠AOC=∠BOD=90°.
(1)若∠DOC=55°,求∠AOD和∠BOC的度数;
(2)试说明:∠AOD=∠BOC.
【答案】解:(1)∵∠AOC=∠BOD=90°,∠DOC=55°,
∴∠AOD=∠AOC-∠DOC=90°-55°=35°,
∠BOC=∠BOD-∠DOC=90°-55°=35°;
(2)∵∠AOD+∠DOC=90°,∠BOC+∠DOC=90°,
∴∠AOD=∠BOC(同角的余角相等).
15. 如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
【答案】解:(1)∵直线AB,CD相交于点O,
∴∠AOC和∠BOD与∠AOD互补.
∵OF平分∠AOE,∴∠AOF=∠EOF,
∵∠DOF=90°,∴∠COF=90°,则∠DOE=∠AOC(等角的余角相等),
∴∠DOE也是∠AOD的补角.
综上,与∠AOD互补的角有∠AOC,∠BOD,∠DOE;
(2)由(1)知∠AOC=∠BOD=∠DOE,
又∵∠AOC+∠AOE+∠DOE=180°,∴∠BOD=∠AOC==30°.
16. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.
【答案】解:(1)∵OE平分∠BOC,∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
故答案为∠BOE、∠COE;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=30°,∠COE=∠BOE=∠BOC,
∴∠AOC=2×30°=60°,∴∠BOC=180°﹣60°=120°,∴∠COE=∠BOC=60°,
∴∠DOE=∠COD+∠COE=90°;
(3)当∠AOD=α°时,∠DOE=90°.
