3.4实际问题与一元一次方程(第4课时)—方案设计问题(电话计费) 课件(共28张PPT)
文档属性
| 名称 | 3.4实际问题与一元一次方程(第4课时)—方案设计问题(电话计费) 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 21:07:45 | ||
图片预览






文档简介
(共28张PPT)
人教版
七上
3.4实际问题与一元一次方程
(第4课时)
——方案设计问题(电话计费)
探究新知
教学重点:
利用数学对生活中(如话费计费)进行优化选择.
教学难点:
分类讨论方案的理解与运用.
情境引入
信息化的时代,手机已成为我们生活中的必需品.打电话、使用流量上网等等都需要相应费用,作为一名消费者,我们该如何选择呢?
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
如下表给出的是两种移动电话的计费方式:
方式一省钱,还是选择方式
二更省钱,你能做出最正确的选择吗?
探究新知
分析:
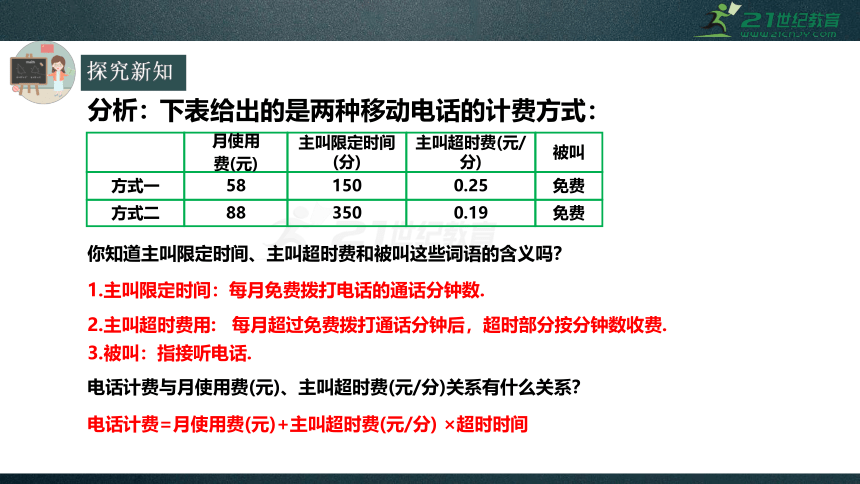
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你知道主叫限定时间、主叫超时费和被叫这些词语的含义吗?
1.主叫限定时间:每月免费拨打电话的通话分钟数.
2.主叫超时费用:
每月超过免费拨打通话分钟后,超时部分按分钟数收费.
3.被叫:指接听电话.
电话计费与月使用费(元)、主叫超时费(元/分)关系有什么关系?
电话计费=月使用费(元)+主叫超时费(元/分)
×超时时间
探究新知
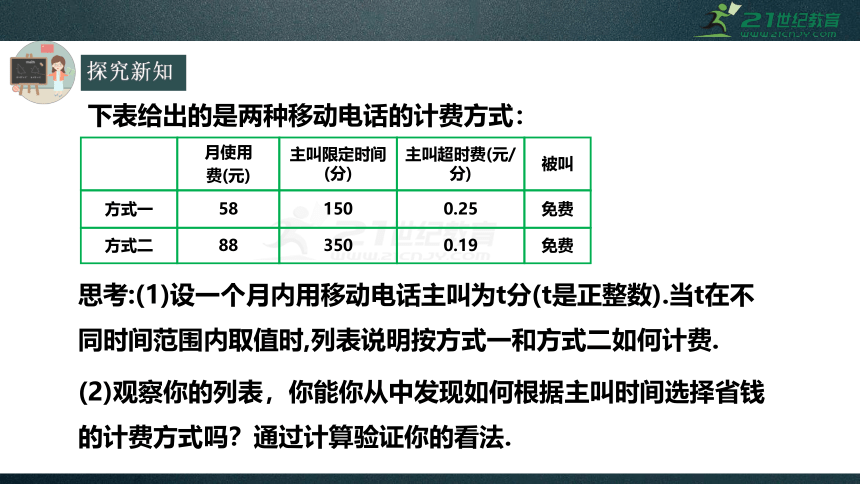
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
思考:(1)设一个月内用移动电话主叫为t分(t是正整数).当t在不同时间范围内取值时,列表说明按方式一和方式二如何计费.
(2)观察你的列表,你能你从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
探究新知
主叫时间t
/分
方式一计费/元
方式二计费/元
t
小于150
t
等于150
t
大于150且小于
350
t
等于350
t
大于350
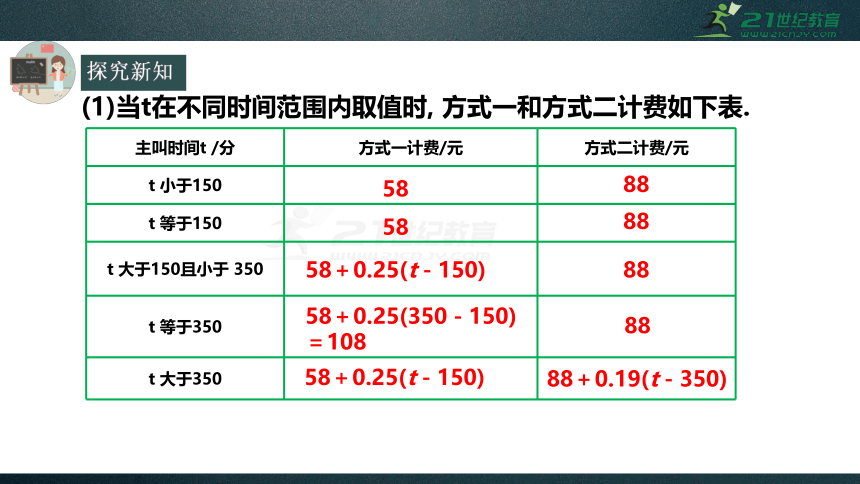
(1)当t在不同时间范围内取值时,
方式一和方式二计费如下表.
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
探究新知
你认为选择哪种计费方式更省钱(设一个月通话分钟数为t,t取正整数)
观察右表得出:
①t小于或等于150时,按方式一的计费小.
思路:当t从150增加到350时,方式一的资费由58增加到108,而方式二的资费一直是88,因此在这一过程中,可能存在方式一和方式二资费相等的情况.
讨论t大于150且小于350,哪个方式计费方式更省钱.
探究新知
58+0.25(t-150)=88
列方程得:
t=270
结论:
①当t=270分钟时,方式一和方式二资费
.
②当150.
③当270.
相同
方式一划算
方式二划算
探究新知
思路:当t大于350时,方式一的计费可以写成108+0.25(t-350)(此时相当月租费为108元,超时部分按0.25收费)
方式一收费:
108+0.25(t-350)
方式二收费:
88+0.19(t-350)
方式一大于方式二资费,方式二划算
因为[108+0.25(t-350)]
–[88+0.19(t-350)]>0
讨论:t大于350
探究新知
综合以上的分析,可以发现:
t小于270时,选择方式一省钱;
t大于270时,选择方式二省钱.
练一练
某市电话拨号上网有两种收费方式,用户可以任选其一.
方式一计时制∶每分钟
0.05
元;
方式二包月制∶每月
60
元(限一部个人住宅电话上网).此外,两种上网方式都得加收通信费每分钟
0.02
元.
(1)某用户某月上网的时间为
x
h,请分别写出两种收费方式下该用户应该支付的费用.
(2)你认为采用哪种方式比较合算?
练一练
分析:确定采用哪种方式比较合算时,应先列方程计算出两种收费方式应支付费用相同时用户的上网时间,再分段讨论,进行比较,得出结论.
解:(1)方式一计时制:(0.05+0.02)×60x=4.2x(元).
方式二包月制:60+0.02×60x=(60+1.2x)(元)
(2)由4.2x=60+1.2x,得x=20.
所以当0时,采用方式一方式合算;
当x=20
时,采用两种方式费用相同;
当x>20
时,采用方式二方式合算.
例题讲解
(补充例题)已知:用1辆A型车和1辆B型车装满货物一次可运货7吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时用A型车a辆和B型车b辆,一次运完,且恰好每辆车都装满货物.
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
例题讲解
解:设1辆A型车都装满货物一次可运货x吨,则1辆B型车都装满货物一次可运货(7-x)吨,根据题意,得
x+2(7-x)=11
解得
x=3
则(7-x)=4
答:1辆A型车和1辆B型车都装满货物一次可分别运货3吨、4吨.
例题讲解
(2)根据题意,得
3a+4b=31
因为a,b都是整数,
所以符合条件的有a=1,b=7;a=5,b=4;a=9,b=1三种情况.
租车方案如下:
①租用A型车1辆,B型车7辆;
②租用A型车5辆,B型车4辆;
③租用A型车9辆,B型车1辆.
例题讲解
方案①租车费100×1+120×7=940元;
方案②租车费100×5+120×4=980元;
方案③租车费100×9+120×4=1020元.
租车费如下:
因为
940<980<1020
故方案①最省钱,即租用A型车1辆,B型车7辆最省钱,最少租车费用为940元.
归纳
解决此问题的关键是分类讨论.解决最优方案问题时,一般采用以下步骤∶
①设未知数;
②列式;
③比较方案;
④决定取舍,即根据比较结果确定最优方案.
课堂练习
1.寒假期间,小刚组织同学一起去看科幻电影《流浪地球》,票价每张45元,20张以上(不含20张)打八折,他们一共花了900元,则他们买到的电影票的张数是( )
A
20
B
22
C
25
D
20或25
2.小明和小红一起拼购购买相同的学习机,甲店承诺若一次购买两台学习机,其中台按原价而另一台可获得七折优惠,乙店承诺若一次购买两台学习机,按总价的80%收费,在哪家店购买学习更优惠(
).
A
乙比甲优惠
B
甲比乙优惠
C
甲乙一样
D
以上都有可能
D
A
课堂练习
3.小明所在城市的“阶梯水价”收费办法如下;每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨如收2元,小明家今年5月份用水9吨,缴纳水费44元,根据题意列出关于x
的方程正确的是(
).
A
5x+4(x+2)=44
B
5x+4(x-2)=44
C
9(x+2)=44
D
9(x+2)-4×2=44
A
课堂练习
4.乘
坐某种出租车,当行驶路程小于或等于3千米时,乘车费用都是
10
元(即起步价
10元),当行驶路程大于3千米时,超过3千米的部分每千米收费2
元(不足1千米按1千米计算).若一次乘坐这种出租车行驶
4千米;则应付车费
元;若一次乘坐这种出租车付费
20
元,则乘车最大路程是
千米.
12
20
课堂练习
5.某公园的门票价格规定如下表:
某校七年级(1)、
(2)两班共有98名学生去公园游玩,其中甲班的人数少于50人,乙班的人数多于50人,若两班都以班为单位分别购票,则共需付款2346元.问:
(1)两班各有多少个学生?
(2)怎样购票最为划算?
课堂练习
解:(1)设甲班有x个学生,则乙班有(98-x)个学生,根据题意得
25x
+23(98-x)=2346
解得x
=46
所以98-x
=52
答:甲班有46个学生,则乙班有52个学生.
课堂练习
(2)两班都以班为单位分别购票,则共需付款2346元.
104×21=2184(元)
2346-2184=162(元)
答:两班作为一个团体购票最为划算,可以省了304元.
若两班作为一个团体购票:
课堂练习
6.甲、乙两家商场出售同样的水瓶和水杯,若购1水瓶和1个水杯总价是48元,购3水瓶和4个水杯总价是152元.甲商场规定:这两种商品都打八折;乙商场规定∶买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若小明想要买5个水瓶和
20
个水杯.
(1)水瓶和水杯单价分别是多少?
(2)请问选择哪家商场购买更合算?并说明理由.(水瓶和水杯必须在同一家商场购买).
课堂练习
理由∶
甲商场所需费用为(40×5+8×20)×80%=288(元);
乙商场所需费用为5×40+(20—5×2)×8=280(元).
因为
288>280,所以选择乙商场购买更合算.
(1)
设水瓶的单价是x
元,
则水杯的单价是(48-x
)
元,根据题意,得
3x+4(48-x
)=152
x=40
(48-x
)=8
课堂小结
1.用方程解决电话计费问题.
2.通过数量关系列方程,并选择合适方案.
谈谈你们这节课有什么收获呢?
课外作业
习题3.4
第107页第10题
第107页第12题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
3.4实际问题与一元一次方程
(第4课时)
——方案设计问题(电话计费)
探究新知
教学重点:
利用数学对生活中(如话费计费)进行优化选择.
教学难点:
分类讨论方案的理解与运用.
情境引入
信息化的时代,手机已成为我们生活中的必需品.打电话、使用流量上网等等都需要相应费用,作为一名消费者,我们该如何选择呢?
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
如下表给出的是两种移动电话的计费方式:
方式一省钱,还是选择方式
二更省钱,你能做出最正确的选择吗?
探究新知
分析:
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你知道主叫限定时间、主叫超时费和被叫这些词语的含义吗?
1.主叫限定时间:每月免费拨打电话的通话分钟数.
2.主叫超时费用:
每月超过免费拨打通话分钟后,超时部分按分钟数收费.
3.被叫:指接听电话.
电话计费与月使用费(元)、主叫超时费(元/分)关系有什么关系?
电话计费=月使用费(元)+主叫超时费(元/分)
×超时时间
探究新知
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
思考:(1)设一个月内用移动电话主叫为t分(t是正整数).当t在不同时间范围内取值时,列表说明按方式一和方式二如何计费.
(2)观察你的列表,你能你从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
探究新知
主叫时间t
/分
方式一计费/元
方式二计费/元
t
小于150
t
等于150
t
大于150且小于
350
t
等于350
t
大于350
(1)当t在不同时间范围内取值时,
方式一和方式二计费如下表.
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
探究新知
你认为选择哪种计费方式更省钱(设一个月通话分钟数为t,t取正整数)
观察右表得出:
①t小于或等于150时,按方式一的计费小.
思路:当t从150增加到350时,方式一的资费由58增加到108,而方式二的资费一直是88,因此在这一过程中,可能存在方式一和方式二资费相等的情况.
讨论t大于150且小于350,哪个方式计费方式更省钱.
探究新知
58+0.25(t-150)=88
列方程得:
t=270
结论:
①当t=270分钟时,方式一和方式二资费
.
②当150
③当270
相同
方式一划算
方式二划算
探究新知
思路:当t大于350时,方式一的计费可以写成108+0.25(t-350)(此时相当月租费为108元,超时部分按0.25收费)
方式一收费:
108+0.25(t-350)
方式二收费:
88+0.19(t-350)
方式一大于方式二资费,方式二划算
因为[108+0.25(t-350)]
–[88+0.19(t-350)]>0
讨论:t大于350
探究新知
综合以上的分析,可以发现:
t小于270时,选择方式一省钱;
t大于270时,选择方式二省钱.
练一练
某市电话拨号上网有两种收费方式,用户可以任选其一.
方式一计时制∶每分钟
0.05
元;
方式二包月制∶每月
60
元(限一部个人住宅电话上网).此外,两种上网方式都得加收通信费每分钟
0.02
元.
(1)某用户某月上网的时间为
x
h,请分别写出两种收费方式下该用户应该支付的费用.
(2)你认为采用哪种方式比较合算?
练一练
分析:确定采用哪种方式比较合算时,应先列方程计算出两种收费方式应支付费用相同时用户的上网时间,再分段讨论,进行比较,得出结论.
解:(1)方式一计时制:(0.05+0.02)×60x=4.2x(元).
方式二包月制:60+0.02×60x=(60+1.2x)(元)
(2)由4.2x=60+1.2x,得x=20.
所以当0
当x=20
时,采用两种方式费用相同;
当x>20
时,采用方式二方式合算.
例题讲解
(补充例题)已知:用1辆A型车和1辆B型车装满货物一次可运货7吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时用A型车a辆和B型车b辆,一次运完,且恰好每辆车都装满货物.
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
例题讲解
解:设1辆A型车都装满货物一次可运货x吨,则1辆B型车都装满货物一次可运货(7-x)吨,根据题意,得
x+2(7-x)=11
解得
x=3
则(7-x)=4
答:1辆A型车和1辆B型车都装满货物一次可分别运货3吨、4吨.
例题讲解
(2)根据题意,得
3a+4b=31
因为a,b都是整数,
所以符合条件的有a=1,b=7;a=5,b=4;a=9,b=1三种情况.
租车方案如下:
①租用A型车1辆,B型车7辆;
②租用A型车5辆,B型车4辆;
③租用A型车9辆,B型车1辆.
例题讲解
方案①租车费100×1+120×7=940元;
方案②租车费100×5+120×4=980元;
方案③租车费100×9+120×4=1020元.
租车费如下:
因为
940<980<1020
故方案①最省钱,即租用A型车1辆,B型车7辆最省钱,最少租车费用为940元.
归纳
解决此问题的关键是分类讨论.解决最优方案问题时,一般采用以下步骤∶
①设未知数;
②列式;
③比较方案;
④决定取舍,即根据比较结果确定最优方案.
课堂练习
1.寒假期间,小刚组织同学一起去看科幻电影《流浪地球》,票价每张45元,20张以上(不含20张)打八折,他们一共花了900元,则他们买到的电影票的张数是( )
A
20
B
22
C
25
D
20或25
2.小明和小红一起拼购购买相同的学习机,甲店承诺若一次购买两台学习机,其中台按原价而另一台可获得七折优惠,乙店承诺若一次购买两台学习机,按总价的80%收费,在哪家店购买学习更优惠(
).
A
乙比甲优惠
B
甲比乙优惠
C
甲乙一样
D
以上都有可能
D
A
课堂练习
3.小明所在城市的“阶梯水价”收费办法如下;每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨如收2元,小明家今年5月份用水9吨,缴纳水费44元,根据题意列出关于x
的方程正确的是(
).
A
5x+4(x+2)=44
B
5x+4(x-2)=44
C
9(x+2)=44
D
9(x+2)-4×2=44
A
课堂练习
4.乘
坐某种出租车,当行驶路程小于或等于3千米时,乘车费用都是
10
元(即起步价
10元),当行驶路程大于3千米时,超过3千米的部分每千米收费2
元(不足1千米按1千米计算).若一次乘坐这种出租车行驶
4千米;则应付车费
元;若一次乘坐这种出租车付费
20
元,则乘车最大路程是
千米.
12
20
课堂练习
5.某公园的门票价格规定如下表:
某校七年级(1)、
(2)两班共有98名学生去公园游玩,其中甲班的人数少于50人,乙班的人数多于50人,若两班都以班为单位分别购票,则共需付款2346元.问:
(1)两班各有多少个学生?
(2)怎样购票最为划算?
课堂练习
解:(1)设甲班有x个学生,则乙班有(98-x)个学生,根据题意得
25x
+23(98-x)=2346
解得x
=46
所以98-x
=52
答:甲班有46个学生,则乙班有52个学生.
课堂练习
(2)两班都以班为单位分别购票,则共需付款2346元.
104×21=2184(元)
2346-2184=162(元)
答:两班作为一个团体购票最为划算,可以省了304元.
若两班作为一个团体购票:
课堂练习
6.甲、乙两家商场出售同样的水瓶和水杯,若购1水瓶和1个水杯总价是48元,购3水瓶和4个水杯总价是152元.甲商场规定:这两种商品都打八折;乙商场规定∶买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若小明想要买5个水瓶和
20
个水杯.
(1)水瓶和水杯单价分别是多少?
(2)请问选择哪家商场购买更合算?并说明理由.(水瓶和水杯必须在同一家商场购买).
课堂练习
理由∶
甲商场所需费用为(40×5+8×20)×80%=288(元);
乙商场所需费用为5×40+(20—5×2)×8=280(元).
因为
288>280,所以选择乙商场购买更合算.
(1)
设水瓶的单价是x
元,
则水杯的单价是(48-x
)
元,根据题意,得
3x+4(48-x
)=152
x=40
(48-x
)=8
课堂小结
1.用方程解决电话计费问题.
2.通过数量关系列方程,并选择合适方案.
谈谈你们这节课有什么收获呢?
课外作业
习题3.4
第107页第10题
第107页第12题
https://www.21cnjy.com/help/help_extract.php
