2.2.1《圆的方程》(苏教版必修2)
文档属性
| 名称 | 2.2.1《圆的方程》(苏教版必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 394.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-30 20:19:08 | ||
图片预览






文档简介
(共25张PPT)
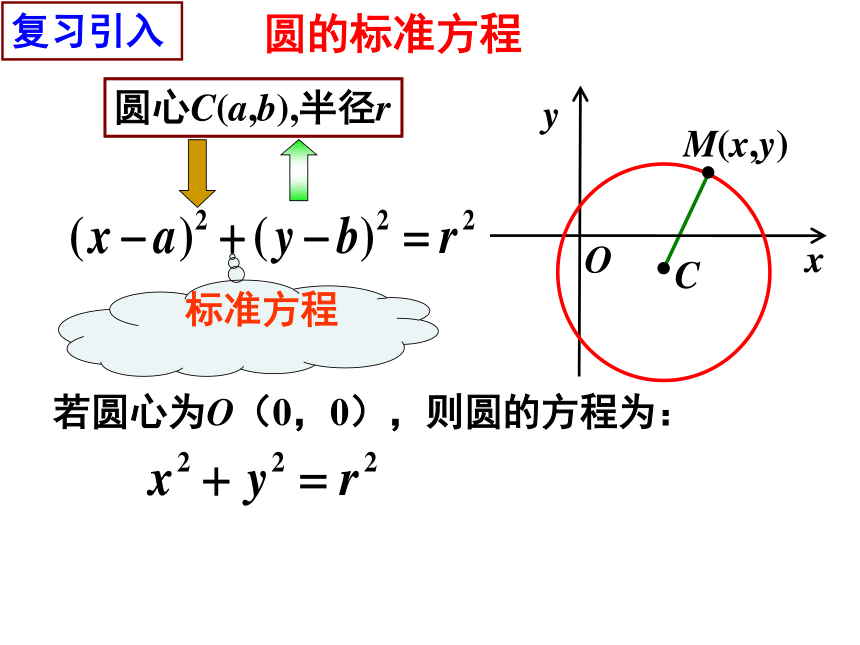
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
复习引入
圆心 (2, -4) ,半径
(6) 圆 (x-2)2+ (y+4)2=2
(7) 圆 (x+1)2+ (y+2)2=m2
圆心 (-1, -2) ,半径|m|
(m≠0)
例1.分别说出下列圆的圆心与半径
复习引入
练1:方程x2+y2=0表示什么图形______
练2:方程(x-1)2=9-(y+3)2表示什么图形
_____________________;
练3:方程y= 表示什么图形
(0,0)
圆心是(1,-3)半径是3的圆
圆心在原点,半径为2的上半圆
_____________________;
复习引入
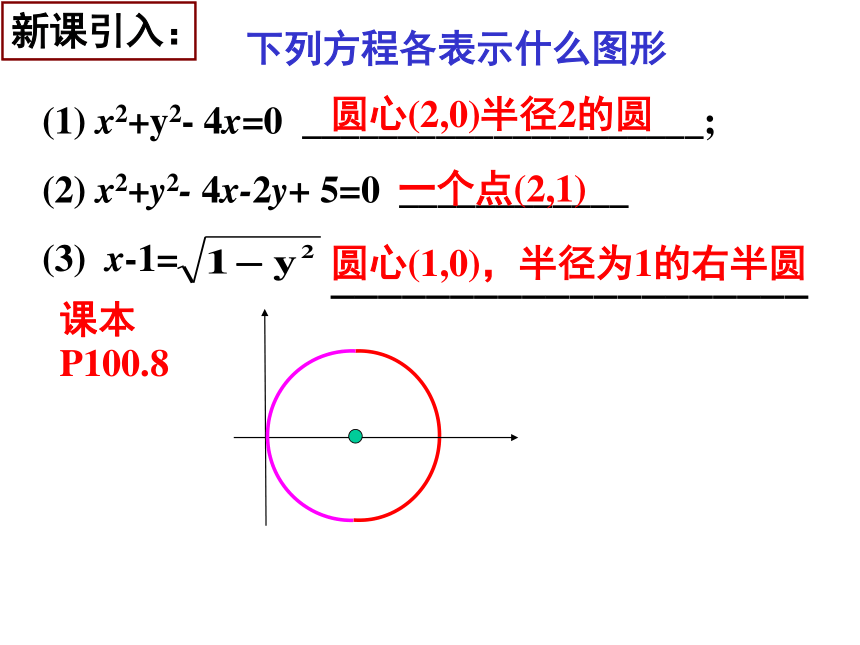
(1) x2+y2- 4x=0 _____________________;
(2) x2+y2- 4x-2y+ 5=0 ____________
(3) x-1=
一个点(2,1)
圆心(2,0)半径2的圆
圆心(1,0),半径为1的右半圆
____________________
下列方程各表示什么图形
课本P100.8
新课引入:
圆的方程一般代数形式是什么特点呢
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
- a
- b
r2
-2ax
-2by
+a2+b2-r2=0
思考
配方得
不一定是圆
以(1,-2)为圆心,以2为半径的圆
配方得
不是圆
思考
圆的一般方程
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
- a
- b
r2
-2ax
-2by
+a2+b2-r2=0
圆的一般方程
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
【排忧解惑】
圆心
·
动画演示
圆心
半径
圆的位置 圆的标准方程 圆的一般方程
原点为圆心
过原点的圆
圆心在x轴上
圆心在y轴上
圆心在x轴上且与y轴相切
圆心在y轴上且与x轴相切
x2+y2=r2
x2+y2+F=0
(x-a)2+(y-b)2=a2+b2
x2+y2+Dx+Ey=0
(x-a)2+y2=r2
x2+y2+Dx+F=0
x2+(y-b)2=r2
x2+y2+Ey+F=0
(x-a)2+y2=a2
x2+y2+Dx=0
x2+(y-b)2=b2
x2+y2+Ey=0
练习:
4
-6
-3
2或-2
(1)已知圆
圆心
半径
(1)圆的一般方程与圆的标准方程的联系:
一般方程
标准方程
(2)给出圆的一般方程,如何求圆心和半径
法一:用配方法;法二:用公式法:
[小结]:
圆心
半径
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
C
A(5,1)
B(7,-3)
D(2,-8)
几何法:
例1:求过A(5,1),B (7,-3),D(2,-8)三点的圆C方程
例1:求过A(5,1),B (7,-3),D(2,-8)三点的圆C方程
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),D(2,-8)都在圆上
所求圆的方程为
A
B
D
H
C
方法三:待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),D(2,-8)都在圆上
所求圆的方程为
课本P99例4
练习:求圆心在直线l:x-2y-2=0上,且过A(0, 4),
B(4, 6)的圆C方程
圆心:两条直线的交点
半径:圆心到圆上一点
C
A(0, 4)
B(4, 6 )
几何法:
设C(a,b),利用CA=CB
C在AB中垂线上
2a+b-9=0
课本P100.8
弦AB的垂直平分线
练习:求圆心在直线l:x-2y-2=0上,且过A(0, 4),
B(4, 6)的圆C方程
C
A(0, 4)
B(4, 6 )
待定系数法
解:设C(a,b),半径r
圆C:(x-a)2+(y-b)2=r2
由题意
同样,可以设所求圆方程为一般式吗?
思考:各个方法的优劣比较?
小结(一)圆的一般方程
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
2、用配方法或公式法由圆的一般式方程求圆心和半径
1、
半径
注意:求圆的方程时,要学会根据题目
条件,恰当选择圆的方程形式:
①涉及圆心和半径,一般采用圆的标准方程
②若已知两点以上,常采用圆的一般方程.
(借助图形几何性质求解简单)
③用待定系数法或几何法求解
④数形结合的思想.
小结(二)如何求圆的方程
小结:求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求 半径
(圆心到圆上一点距离)
写出圆的标准方程
待定系数法
列关于a,b,r(或D,E,F)的方程组
解出a,b,r(或D,E,F),写出标准方程(或一般方程)
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
复习引入
圆心 (2, -4) ,半径
(6) 圆 (x-2)2+ (y+4)2=2
(7) 圆 (x+1)2+ (y+2)2=m2
圆心 (-1, -2) ,半径|m|
(m≠0)
例1.分别说出下列圆的圆心与半径
复习引入
练1:方程x2+y2=0表示什么图形______
练2:方程(x-1)2=9-(y+3)2表示什么图形
_____________________;
练3:方程y= 表示什么图形
(0,0)
圆心是(1,-3)半径是3的圆
圆心在原点,半径为2的上半圆
_____________________;
复习引入
(1) x2+y2- 4x=0 _____________________;
(2) x2+y2- 4x-2y+ 5=0 ____________
(3) x-1=
一个点(2,1)
圆心(2,0)半径2的圆
圆心(1,0),半径为1的右半圆
____________________
下列方程各表示什么图形
课本P100.8
新课引入:
圆的方程一般代数形式是什么特点呢
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
- a
- b
r2
-2ax
-2by
+a2+b2-r2=0
思考
配方得
不一定是圆
以(1,-2)为圆心,以2为半径的圆
配方得
不是圆
思考
圆的一般方程
展开得
任何一个圆的方程都是二元二次方程
反之是否成立?
- a
- b
r2
-2ax
-2by
+a2+b2-r2=0
圆的一般方程
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
【排忧解惑】
圆心
·
动画演示
圆心
半径
圆的位置 圆的标准方程 圆的一般方程
原点为圆心
过原点的圆
圆心在x轴上
圆心在y轴上
圆心在x轴上且与y轴相切
圆心在y轴上且与x轴相切
x2+y2=r2
x2+y2+F=0
(x-a)2+(y-b)2=a2+b2
x2+y2+Dx+Ey=0
(x-a)2+y2=r2
x2+y2+Dx+F=0
x2+(y-b)2=r2
x2+y2+Ey+F=0
(x-a)2+y2=a2
x2+y2+Dx=0
x2+(y-b)2=b2
x2+y2+Ey=0
练习:
4
-6
-3
2或-2
(1)已知圆
圆心
半径
(1)圆的一般方程与圆的标准方程的联系:
一般方程
标准方程
(2)给出圆的一般方程,如何求圆心和半径
法一:用配方法;法二:用公式法:
[小结]:
圆心
半径
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
C
A(5,1)
B(7,-3)
D(2,-8)
几何法:
例1:求过A(5,1),B (7,-3),D(2,-8)三点的圆C方程
例1:求过A(5,1),B (7,-3),D(2,-8)三点的圆C方程
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),D(2,-8)都在圆上
所求圆的方程为
A
B
D
H
C
方法三:待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),D(2,-8)都在圆上
所求圆的方程为
课本P99例4
练习:求圆心在直线l:x-2y-2=0上,且过A(0, 4),
B(4, 6)的圆C方程
圆心:两条直线的交点
半径:圆心到圆上一点
C
A(0, 4)
B(4, 6 )
几何法:
设C(a,b),利用CA=CB
C在AB中垂线上
2a+b-9=0
课本P100.8
弦AB的垂直平分线
练习:求圆心在直线l:x-2y-2=0上,且过A(0, 4),
B(4, 6)的圆C方程
C
A(0, 4)
B(4, 6 )
待定系数法
解:设C(a,b),半径r
圆C:(x-a)2+(y-b)2=r2
由题意
同样,可以设所求圆方程为一般式吗?
思考:各个方法的优劣比较?
小结(一)圆的一般方程
(1)当 时,
表示圆,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
2、用配方法或公式法由圆的一般式方程求圆心和半径
1、
半径
注意:求圆的方程时,要学会根据题目
条件,恰当选择圆的方程形式:
①涉及圆心和半径,一般采用圆的标准方程
②若已知两点以上,常采用圆的一般方程.
(借助图形几何性质求解简单)
③用待定系数法或几何法求解
④数形结合的思想.
小结(二)如何求圆的方程
小结:求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求 半径
(圆心到圆上一点距离)
写出圆的标准方程
待定系数法
列关于a,b,r(或D,E,F)的方程组
解出a,b,r(或D,E,F),写出标准方程(或一般方程)
