人教版九年级数学24.2直线和圆的位置关系同步练习题(Word版 含解析)
文档属性
| 名称 | 人教版九年级数学24.2直线和圆的位置关系同步练习题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 182.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览


文档简介
人教版九年级数学24.2直线和圆的位置关系同步练习题
姓名:__________
班级:__________考号:__________
题号
一
二
三
总分
评分
?
?
?
?
一、单选题(共11题;共22分)
1.如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为(??
)
A.?10
?????????????????????????????????????B.?15?????????????????????????????????????C.?10
?????????????????????????????????????D.?20
2.如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为(??
)
A.?10
?????????????????????????????????????B.?15?????????????????????????????????????C.?10
?????????????????????????????????????D.?20
3.如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB的度数为(??
)
A.?65°???????????????????????????????????????B.?55°???????????????????????????????????????C.?45°???????????????????????????????????????D.?35°
4.已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是(??
)
A.?d=3??????????????????????????????????B.?d>3??????????????????????????????????C.?0≤d<3??????????????????????????????????D.?d<3
5.如图,
是
的弦,点
在过点
的切线上,
,
交
于点
.若
,则
的度数等于(??
)
A.??????????????B.????????????????????????C.????????????????????????????D.?
6.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
A.?120°????????????????????????????????????B.?125°????????????????????????????????????C.?130°????????????????????????????????????D.?135°
7.如图所示,在直角坐标系中,A点坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为(??
)
A.?(-3,0)???????????B.?(-2,0)???????????C.?(-4,0)或(-2,0)??????????????D.?(-4,0)
8.在平面直角坐标系xOy中,以点(3,4)为圆心,4为半径的圆与y轴( )
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
9.在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆必定( )
A.?与x轴相切、与y轴相离
B.?与x轴、y轴都相离
C.?与x轴相离、与y轴相切
D.?与x轴、y轴都相切
10.已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是(?????
)
A.?11??????????????????????????????????????????B.?10??????????????????????????????????????????C.?9??????????????????????????????????????????D.?8
11.如图已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,
DC是⊙O的切线,C是切点,连结AC,若∠CAB=30°
,
则BD的长为(??
)
A.?R???????????????????????????????????????B.?R???????????????????????????????????????C.?2R???????????????????????????????????????D.?R
二、填空题(共11题;共11分)
12.已知⊙O的半径为5,圆心O到直线l的距离为4,则⊙O与直线l的位置关系为________
13.如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°.
(
第15题
)
(
第13题
)
14.在
中,
,
,
,则
的内切圆的半径为________.
15.如图,直线a⊥b,垂足为
,点
在直线
上,
,
为直线
上一动点,若以
为半径的
与直线
相切,则
的长为________.
16.Rt△ABC中,∠C=90°,若直角边AC=5,BC=12,则此三角形的内切圆半径为________.
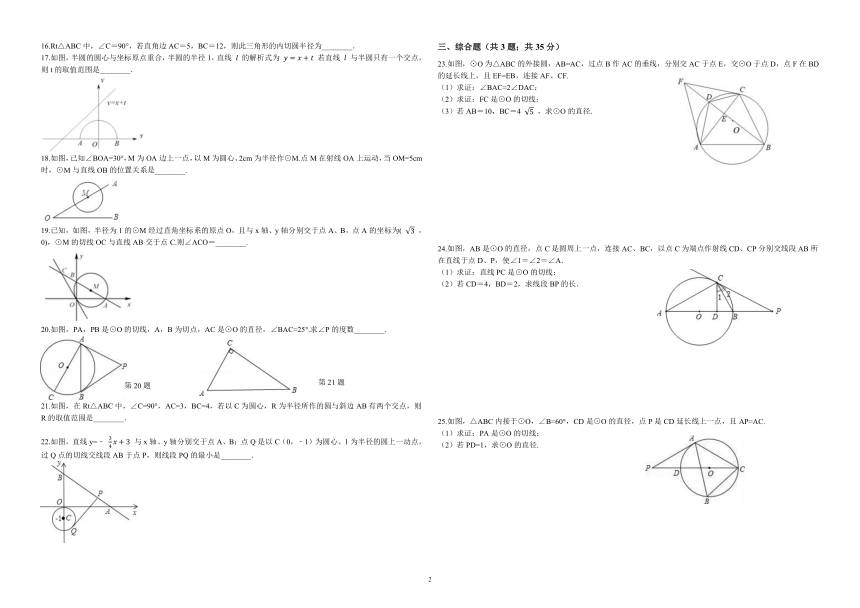
17.如图,半圆的圆心与坐标原点重合,半圆的半径1,直线
的解析式为
若直线
与半圆只有一个交点,则t的取值范围是________.
18.如图,已知∠BOA=30°,M为OA边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OA上运动,当OM=5cm时,⊙M与直线OB的位置关系是________.
19.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(
,0),⊙M的切线OC与直线AB交于点C.则∠ACO=________.
20.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC=25°.求∠P的度数________.
(
第21题
)
(
第20题
)
21.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB有两个交点,则R的取值范围是________.
22.如图,直线y=﹣
与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是________.
三、综合题(共3题;共35分)
23.如图,⊙O为△ABC的外接圆,AB=AC,过点B作AC的垂线,分别交AC于点E,交⊙O于点D,点F在BD的延长线上,且EF=EB,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)求证:FC是⊙O的切线;
(3)若AB=10,BC=4
,求⊙O的直径.
24.如图,AB是⊙O的直径,点C是圆周上一点,连接AC、BC,以点C为端点作射线CD、CP分别交线段AB所在直线于点D、P,使∠1=∠2=∠A.
(1)求证:直线PC是⊙O的切线;
(2)若CD=4,BD=2,求线段BP的长.
25.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=1,求⊙O的直径.
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:∵AE切⊙D于点E,
∴∠AED=90°,
∵AC=CD=DB=10,
∴AD=20,DE=10,
∴AE=
.
故答案为:C.
【分析】根据切线的性质得∠AED=90°,然后利用已知条件根据勾股定理即可求出AE.
2.【答案】
C
【解析】【解答】解:∵AE切⊙D于点E,
∴∠AED=90°,
∵AC=CD=DB=10,
∴AD=20,DE=10,
∴AE=
.
故答案为:C.
【分析】根据切线的性质得∠AED=90°,然后利用已知条件根据勾股定理即可求出AE.
3.【答案】
B
【解析】【解答】解:∵AB是⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,
∴∠AOB=90°﹣∠B=55°,
故答案为:B.
【分析】根据切线性质:圆的切线垂直于过切点的半径可得∠A=90°,根据直角三角形两锐角互余即可计算∠AOB.
4.【答案】
C
【解析】【解答】∵⊙O的半径为3,直线l与⊙O相交,
∴圆心D到直线l的距离d的取值范围是0≤d<3,
故答案为:C.
【分析】根据直线l和⊙O相交?d<r,即可判断.
5.【答案】
B
【解析】【解答】解:∵
,
∴∠APO=70°,
∵
,
∴∠AOP=90°,∴∠A=20°,
又∵OA=OB,
∴∠ABO=20°,
又∵点C在过点B的切线上,
∴∠OBC=90°,
∴∠ABC=∠OBC?∠ABO=90°?20°=70°,
故答案为:B.
【分析】根据题意可求出∠APO、∠A的度数,进一步可得∠ABO度数,从而推出答案.
6.【答案】
B
【解析】【解答】解:∵O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°﹣∠A)=
(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故答案为:B.
【分析】利用内心的性质得∠OBC=
∠ABC,∠OCB=
∠ACB,再根据三角形内角和计算出∠OBC+∠OCB=55°,然后再利用三角形内角和计算∠BOC的度数.
7.【答案】
A
【解析】【解答】连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
则根据垂线段最短,则作AP⊥x轴于P,即为所求作的点P;
此时P点的坐标是(-3,0).
故答案为:A.
【分析】此题根据切线的性质以及勾股定理,把要求PQ的最小值转化为求AP的最小值,再根据垂线段最短的性质进行分析求解.
8.【答案】
A
【解析】【解答】解:由题意得:圆心到y轴的距离为3,
∵3<半径4,
∴圆与y轴相交.
故答案为:A
【分析】先找出圆心到y轴的距离,再与圆的半径进行比较,若圆心到y轴的距离小于半径,则圆与y轴相交,反之相离,若二者相等则相切.
9.【答案】
A
【解析】【解答】解:∵点(2,1)到x轴的距离是1,到y轴的距离是2,
∴在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆必定与x轴相切,与y轴相离,
故答案为:A
.
【分析】先求出点(2,1)到x轴的距离是1,到y轴的距离是2,再根据直线与圆的位置关系的内容得出即可.
10.【答案】
C
【解析】【解答】设⊙A的半径为X,⊙B的半径为Y,⊙C的半径为Z.
解得
故答案为:C
【分析】根据圆的切线的性质,即可得到X,Y,Z之间的关系,根据其关系计算得到圆的半径的长度即可。
11.【答案】
A
【解析】【解答】连接OC,BC,
∵AB是圆O的直径,DC是圆O的切线,C是切点,
∴∠ACB=∠OCD=90°,
∵∠CAB=30°,
∴∠COD=2∠A=60°,CD=OC?tan∠COD=
R,
由切割线定理得,CD2=BD?AD=BD(BD+AB),
∴BD=R.
故选A.
【分析】先利用“同弧所对的圆周角是圆心角的一半”得出∠COD=2∠A=60°,再解直角三角形可得CD长,最后用切割线定理可得BD长。
二、填空题
12.【答案】
相交
【解析】【解答】直线与圆的位置关系来判定:①直线l和⊙O相交?d<r;②直线l和⊙O相切?d=r;③直线l和⊙O相离?d>r(d为直线与圆的距离,r为圆的半径).因此,
∵⊙O的半径为5,圆心O到直线l的距离为34,
∵5>4,即:d<r,∴直线l与⊙O的位置关系是相交.
故答案是:相交
【分析】根据直线与圆的位置关系,比较半径r与直线到圆的距离d,即可解决.
13.【答案】
120
【解析】【解答】解:∵AC与⊙O相切,
∴∠BAC=90°,
∵∠CAD=30°,
∴∠OAD=60°,
∴∠BOD=2∠BAD=120°,
故答案为:120.
【分析】根据切线的性质求出∠BAC=90°,再求出∠OAD=60°,根据圆周角定理得出∠BOD=2∠BAD,代入即可求出∠BOD的值.
14.【答案】
1
【解析】【解答】如图,设△ABC的内切圆与各边相切于D,E,F,连接OD,OE,OF,
则OE⊥BC,OF⊥AB,OD⊥AC,
设半径为r,CD=r,
∵∠C=90°,BC=4,AC=3,
∴AB=5,
∴BE=BF=4-r,AF=AD=3-r,
∴4-r+3-r=5,
∴r=1.
∴△ABC的内切圆的半径为
1.
故答案为:1.
【分析】根据勾股定理可以得出AB=5,根据切线长定理得出BE=BF=4-r,AF=AD=3-r,则AB=4-r+3-r=5,进而得出r=1,即半径为1。
15.【答案】
3或5
【解析】【解答】解:∵a⊥b
∴
与直线
相切,OH=1
当
在直线a的左侧时,OP=PH-OH=4-1=3;
当
在直线a的右侧时,OP=PH+OH=4+1=5;
故答案为3或5.
【分析】根据切线的性质可得OH=1,故OP=PH-OH或OP=PH+OH,即可得解.
16.【答案】
2
【解析】【解答】解:如图;
在Rt△ABC,∠C=90°,AC=5,BC=12;
根据勾股定理AB=
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形;
由切线长定理,得:AD=AE,BD=BF,CE=CF;
∴CE=CF=
(AC+BC-AB);
即:r=
(5+12-13)=2.
故答案为2.
【分析】设AB、BC、AC与⊙O的切点分别为D、F、E;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF=
(AC+BC-AB),由此可求出r的长.
17.【答案】
或
【解析】【解答】若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线A开始到直线过点B结束(不包括直线过点A)
当直线和半圆相切于点C时,直线与x轴所形成的的锐角是45°,
∴∠DOC=45°,
又∵半圆的半径1,
∴CD=OD=
∴
代入解析式,得
当直线过点A时,把A代入直线解析式,得
当直线过点B时,把B代入直线解析式,得
即当
或
,直线和半圆只有一个交点.
【分析】若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线A开始到直线过点B结束(不包括直线过点A),当直线和半圆相切于点C时,根据直线的解析式知直线与x轴所形成的的锐角是45°,从而求得∠DOC=45°,即可得出点C的坐标,进一步得出t的值;当直线过点B时,直线根据待定系数法求得t的值.
18.【答案】
相离
【解析】【解答】作MH⊥OA于H,如图,
在Rt△OMH中,∵∠HOM=30°,
∴MH=
OM=
,
∵⊙M的半径为2,
∴MH>2,
∴⊙M与直线OB的位置关系是相是离.
故答案为相离.
【分析】作MH⊥OA于H,在Rt△OMH中,30度角所对的直角边等于斜边的一半可得MH=OM,把MH的值与半径2比较大小,根据直线与圆的位置关系,当圆心到直线的距离大于半径时,直线与圆相离可判断求解。
19.【答案】
30°
【解析】【解答】连接MO,作MD⊥OA,
∴AD=
OA=
,
MD=
=
,
∠MAO=30°,
又MA=OA,∴∠MOA=∠MAO=30°,
又OC是⊙M的切线,
∴∠MOC=90°,∠AOC=∠MOC+∠MCO=120°,
∴∠ACO=180°-∠AOC-∠MAO=180°-120°-30°=30°。
故答案为:30°。
【分析】由垂径定理和切线的性质可求出∠MAO和∠AOC的度数,再根据三角形内角和定理即可求出∠ACO的度数。
20.【答案】
50
【解析】【解答】∵PA、PB是⊙O的切线,
∴PA=PB,
∴∠PAB=∠PBA,
∵AC是⊙O的直径,PA是⊙O的切线,
∴AC⊥AP,
∴∠CAP=90°,
∵∠BAC=25°,
∴∠PBA=∠PAB=90°﹣25°=65°,
∴∠P=180°﹣∠PAB﹣∠PBA=180°﹣65°﹣65°=50°.
【分析】根据切线性质得出PA=PB,∠PAO=90°,求出∠PAB的度数,得出∠PAB=∠PBA,根据三角形的内角和定理求出即可.
21.【答案】
2.4<R≤3
【解析】【解答】解:如图,
∵BC>AC,
∴以C为圆心,R为半径所作的圆与斜边AB有两个交点,则圆的半径应大于CD,小于或等于AC,
由勾股定理知,AB=
?=5.
∵S△ABC=
?AC?BC=
?CD?AB=
×3×4=
×5?CD,
∴CD=2.4,
即R的取值范围是2.4<R≤3.
【分析】以C为圆心,R为半径所作的圆与斜边AB有两个交点,故AB与该圆相交,则圆的半径应大于CD,小于或等于AC,由勾股定理算出AB,根据三角形的面积法算出CD,从而得出答案。
22.【答案】
【解析】【解答】解:过点C作CP⊥直线AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.
直线AB的解析式为y=﹣
,即3x+4y﹣12=0,
∴CP=
=
.
∵PQ为⊙C的切线,
∴在Rt△CQP中,CQ=1,∠CQP=90°,
∴PQ=
=
.
故答案为:
.
【分析】过点C作CP⊥直线AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,由点到直线的距离求出CP的长度,再根据勾股定理即可求出PQ的长度.本题考查了切线的性质、点到直线的距离以及勾股定理,解题的关键是确定P、Q点的位置.本题属于中档题,难度不大,解决该题型题目时,借助于切线的性质寻找到PQ取最小值时点P、Q的位置是关键.
三、综合题
23.【答案】
(1)证明:∵AB=AC
∴∠ABC=∠ACB
∴∠CAB=180°-2∠ACB
∵BD⊥AC
∴∠BEC=90°,∠DBC+∠ACB=90°
∴∠DBC=90°-∠ACB
∵∠DAC=∠DBC=90°-∠ACB
∴2∠DAC=2(90°-∠ACB)=180°-2∠ACB
∴∠CAB=2∠DAC
(2)解:⊙O的直径CG,连结BG,
∵EF=EB,BD⊥AC
∴CF=CB
∴∠CFD=∠CBD,∠CAB=∠CDB=∠CFD+∠FCD=∠CBD+∠FCD
又由(1)可知∠CAB=2∠DAC=2∠CBD
∴∠FCD=∠CBD=∠CFD
∵CG为直径
∴∠CBG=90°
∴∠FCG=∠FCD+∠DCG=∠CBD+∠DBG=90°
∴FC⊥CG
∵CG为直径
∴FC为⊙O的切线
(3)解:∵AC=AB=10,BC=4
∴设
,
,
∴
,
∴AE=6,CE=4,BE=
8
∵∠CGB=∠EAB
∴sin∠CGB=
=sin∠EAB=
∴CG=
【解析】【分析】(1)根据切线的性质,可换算得出角度关系。
(2)根据切线的判定定理,可判定。
(3)利用勾股定理可解出直径。
24.【答案】
(1)解:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
∵OA=OC,
∴∠A=∠ACO,
∵∠A=∠1=∠2,
∴∠2=∠ACO,
∴∠2+∠BCO=90°,
∴∠PCO=90°,
∴OC⊥PC,
∴直线PC是⊙O的切线;
(2)解:∵∠ACB=90°,
∴∠A+∠ABC=90°
∴∠1=∠A,
∴∠1+∠ABC=90°,
∴∠CDB=90°,
∴CD2=AD?BD,
∵CD=4,BD=2,
∴AD=8,
∴AB=10,
∴OC=OB=5,
∵∠OCP=90°,CD⊥OP,
∴OC2=OD?OP,
∴52=(5﹣2)×OP,
∴OP=
,
∴PB=OP﹣OB=
.
【解析】【分析】(1)连接OC,由AB是⊙O的直径证得∠ACO+∠BCO=90°,由OA=OC证得∠2=∠A=∠ACO,由此得到∠PCO=90°,即证得直线PC是⊙O的切线;(2)利用∠1=∠A证得∠CDB=90°,得到CD2=AD?BD,求出AD,由此求得AB=10,OB=5;再由∠OCP=90°推出OC2=OD?OP,求出OP=
,由此求得线段BP的长.
25.【答案】
(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(2)解:设该圆的半径为x.
在Rt△OAP中,∵∠P=30°,
∴PO=2OA=OD+PD,又∵OA=OD,
∴1+x=2x,解得:x=1
∴OA=PD=1,
所以⊙O的直径为2.
【解析】【分析】(1)连接OA,根据圆周角定理首先求得∠AOC的度数,然后根据等腰三角形的性质求得∠OAP=90°,从而求解;(2)根据直角三角形的性质,直角三角形中30°所对的边等于斜边的一半,即可求解.
(
2
)
(
1
)
姓名:__________
班级:__________考号:__________
题号
一
二
三
总分
评分
?
?
?
?
一、单选题(共11题;共22分)
1.如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为(??
)
A.?10
?????????????????????????????????????B.?15?????????????????????????????????????C.?10
?????????????????????????????????????D.?20
2.如图所示,AE切⊙D于点E,AC=CD=DB=10,则线段AE的长为(??
)
A.?10
?????????????????????????????????????B.?15?????????????????????????????????????C.?10
?????????????????????????????????????D.?20
3.如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB的度数为(??
)
A.?65°???????????????????????????????????????B.?55°???????????????????????????????????????C.?45°???????????????????????????????????????D.?35°
4.已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是(??
)
A.?d=3??????????????????????????????????B.?d>3??????????????????????????????????C.?0≤d<3??????????????????????????????????D.?d<3
5.如图,
是
的弦,点
在过点
的切线上,
,
交
于点
.若
,则
的度数等于(??
)
A.??????????????B.????????????????????????C.????????????????????????????D.?
6.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
A.?120°????????????????????????????????????B.?125°????????????????????????????????????C.?130°????????????????????????????????????D.?135°
7.如图所示,在直角坐标系中,A点坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为(??
)
A.?(-3,0)???????????B.?(-2,0)???????????C.?(-4,0)或(-2,0)??????????????D.?(-4,0)
8.在平面直角坐标系xOy中,以点(3,4)为圆心,4为半径的圆与y轴( )
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
9.在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆必定( )
A.?与x轴相切、与y轴相离
B.?与x轴、y轴都相离
C.?与x轴相离、与y轴相切
D.?与x轴、y轴都相切
10.已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是(?????
)
A.?11??????????????????????????????????????????B.?10??????????????????????????????????????????C.?9??????????????????????????????????????????D.?8
11.如图已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,
DC是⊙O的切线,C是切点,连结AC,若∠CAB=30°
,
则BD的长为(??
)
A.?R???????????????????????????????????????B.?R???????????????????????????????????????C.?2R???????????????????????????????????????D.?R
二、填空题(共11题;共11分)
12.已知⊙O的半径为5,圆心O到直线l的距离为4,则⊙O与直线l的位置关系为________
13.如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=________°.
(
第15题
)
(
第13题
)
14.在
中,
,
,
,则
的内切圆的半径为________.
15.如图,直线a⊥b,垂足为
,点
在直线
上,
,
为直线
上一动点,若以
为半径的
与直线
相切,则
的长为________.
16.Rt△ABC中,∠C=90°,若直角边AC=5,BC=12,则此三角形的内切圆半径为________.
17.如图,半圆的圆心与坐标原点重合,半圆的半径1,直线
的解析式为
若直线
与半圆只有一个交点,则t的取值范围是________.
18.如图,已知∠BOA=30°,M为OA边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OA上运动,当OM=5cm时,⊙M与直线OB的位置关系是________.
19.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(
,0),⊙M的切线OC与直线AB交于点C.则∠ACO=________.
20.如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC=25°.求∠P的度数________.
(
第21题
)
(
第20题
)
21.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径所作的圆与斜边AB有两个交点,则R的取值范围是________.
22.如图,直线y=﹣
与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是________.
三、综合题(共3题;共35分)
23.如图,⊙O为△ABC的外接圆,AB=AC,过点B作AC的垂线,分别交AC于点E,交⊙O于点D,点F在BD的延长线上,且EF=EB,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)求证:FC是⊙O的切线;
(3)若AB=10,BC=4
,求⊙O的直径.
24.如图,AB是⊙O的直径,点C是圆周上一点,连接AC、BC,以点C为端点作射线CD、CP分别交线段AB所在直线于点D、P,使∠1=∠2=∠A.
(1)求证:直线PC是⊙O的切线;
(2)若CD=4,BD=2,求线段BP的长.
25.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=1,求⊙O的直径.
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:∵AE切⊙D于点E,
∴∠AED=90°,
∵AC=CD=DB=10,
∴AD=20,DE=10,
∴AE=
.
故答案为:C.
【分析】根据切线的性质得∠AED=90°,然后利用已知条件根据勾股定理即可求出AE.
2.【答案】
C
【解析】【解答】解:∵AE切⊙D于点E,
∴∠AED=90°,
∵AC=CD=DB=10,
∴AD=20,DE=10,
∴AE=
.
故答案为:C.
【分析】根据切线的性质得∠AED=90°,然后利用已知条件根据勾股定理即可求出AE.
3.【答案】
B
【解析】【解答】解:∵AB是⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,
∴∠AOB=90°﹣∠B=55°,
故答案为:B.
【分析】根据切线性质:圆的切线垂直于过切点的半径可得∠A=90°,根据直角三角形两锐角互余即可计算∠AOB.
4.【答案】
C
【解析】【解答】∵⊙O的半径为3,直线l与⊙O相交,
∴圆心D到直线l的距离d的取值范围是0≤d<3,
故答案为:C.
【分析】根据直线l和⊙O相交?d<r,即可判断.
5.【答案】
B
【解析】【解答】解:∵
,
∴∠APO=70°,
∵
,
∴∠AOP=90°,∴∠A=20°,
又∵OA=OB,
∴∠ABO=20°,
又∵点C在过点B的切线上,
∴∠OBC=90°,
∴∠ABC=∠OBC?∠ABO=90°?20°=70°,
故答案为:B.
【分析】根据题意可求出∠APO、∠A的度数,进一步可得∠ABO度数,从而推出答案.
6.【答案】
B
【解析】【解答】解:∵O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°﹣∠A)=
(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故答案为:B.
【分析】利用内心的性质得∠OBC=
∠ABC,∠OCB=
∠ACB,再根据三角形内角和计算出∠OBC+∠OCB=55°,然后再利用三角形内角和计算∠BOC的度数.
7.【答案】
A
【解析】【解答】连接AQ,AP.
根据切线的性质定理,得AQ⊥PQ;
要使PQ最小,只需AP最小,
则根据垂线段最短,则作AP⊥x轴于P,即为所求作的点P;
此时P点的坐标是(-3,0).
故答案为:A.
【分析】此题根据切线的性质以及勾股定理,把要求PQ的最小值转化为求AP的最小值,再根据垂线段最短的性质进行分析求解.
8.【答案】
A
【解析】【解答】解:由题意得:圆心到y轴的距离为3,
∵3<半径4,
∴圆与y轴相交.
故答案为:A
【分析】先找出圆心到y轴的距离,再与圆的半径进行比较,若圆心到y轴的距离小于半径,则圆与y轴相交,反之相离,若二者相等则相切.
9.【答案】
A
【解析】【解答】解:∵点(2,1)到x轴的距离是1,到y轴的距离是2,
∴在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆必定与x轴相切,与y轴相离,
故答案为:A
.
【分析】先求出点(2,1)到x轴的距离是1,到y轴的距离是2,再根据直线与圆的位置关系的内容得出即可.
10.【答案】
C
【解析】【解答】设⊙A的半径为X,⊙B的半径为Y,⊙C的半径为Z.
解得
故答案为:C
【分析】根据圆的切线的性质,即可得到X,Y,Z之间的关系,根据其关系计算得到圆的半径的长度即可。
11.【答案】
A
【解析】【解答】连接OC,BC,
∵AB是圆O的直径,DC是圆O的切线,C是切点,
∴∠ACB=∠OCD=90°,
∵∠CAB=30°,
∴∠COD=2∠A=60°,CD=OC?tan∠COD=
R,
由切割线定理得,CD2=BD?AD=BD(BD+AB),
∴BD=R.
故选A.
【分析】先利用“同弧所对的圆周角是圆心角的一半”得出∠COD=2∠A=60°,再解直角三角形可得CD长,最后用切割线定理可得BD长。
二、填空题
12.【答案】
相交
【解析】【解答】直线与圆的位置关系来判定:①直线l和⊙O相交?d<r;②直线l和⊙O相切?d=r;③直线l和⊙O相离?d>r(d为直线与圆的距离,r为圆的半径).因此,
∵⊙O的半径为5,圆心O到直线l的距离为34,
∵5>4,即:d<r,∴直线l与⊙O的位置关系是相交.
故答案是:相交
【分析】根据直线与圆的位置关系,比较半径r与直线到圆的距离d,即可解决.
13.【答案】
120
【解析】【解答】解:∵AC与⊙O相切,
∴∠BAC=90°,
∵∠CAD=30°,
∴∠OAD=60°,
∴∠BOD=2∠BAD=120°,
故答案为:120.
【分析】根据切线的性质求出∠BAC=90°,再求出∠OAD=60°,根据圆周角定理得出∠BOD=2∠BAD,代入即可求出∠BOD的值.
14.【答案】
1
【解析】【解答】如图,设△ABC的内切圆与各边相切于D,E,F,连接OD,OE,OF,
则OE⊥BC,OF⊥AB,OD⊥AC,
设半径为r,CD=r,
∵∠C=90°,BC=4,AC=3,
∴AB=5,
∴BE=BF=4-r,AF=AD=3-r,
∴4-r+3-r=5,
∴r=1.
∴△ABC的内切圆的半径为
1.
故答案为:1.
【分析】根据勾股定理可以得出AB=5,根据切线长定理得出BE=BF=4-r,AF=AD=3-r,则AB=4-r+3-r=5,进而得出r=1,即半径为1。
15.【答案】
3或5
【解析】【解答】解:∵a⊥b
∴
与直线
相切,OH=1
当
在直线a的左侧时,OP=PH-OH=4-1=3;
当
在直线a的右侧时,OP=PH+OH=4+1=5;
故答案为3或5.
【分析】根据切线的性质可得OH=1,故OP=PH-OH或OP=PH+OH,即可得解.
16.【答案】
2
【解析】【解答】解:如图;
在Rt△ABC,∠C=90°,AC=5,BC=12;
根据勾股定理AB=
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形;
由切线长定理,得:AD=AE,BD=BF,CE=CF;
∴CE=CF=
(AC+BC-AB);
即:r=
(5+12-13)=2.
故答案为2.
【分析】设AB、BC、AC与⊙O的切点分别为D、F、E;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF=
(AC+BC-AB),由此可求出r的长.
17.【答案】
或
【解析】【解答】若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线A开始到直线过点B结束(不包括直线过点A)
当直线和半圆相切于点C时,直线与x轴所形成的的锐角是45°,
∴∠DOC=45°,
又∵半圆的半径1,
∴CD=OD=
∴
代入解析式,得
当直线过点A时,把A代入直线解析式,得
当直线过点B时,把B代入直线解析式,得
即当
或
,直线和半圆只有一个交点.
【分析】若直线与半圆只有一个交点,则有两种情况:直线和半圆相切于点C或从直线A开始到直线过点B结束(不包括直线过点A),当直线和半圆相切于点C时,根据直线的解析式知直线与x轴所形成的的锐角是45°,从而求得∠DOC=45°,即可得出点C的坐标,进一步得出t的值;当直线过点B时,直线根据待定系数法求得t的值.
18.【答案】
相离
【解析】【解答】作MH⊥OA于H,如图,
在Rt△OMH中,∵∠HOM=30°,
∴MH=
OM=
,
∵⊙M的半径为2,
∴MH>2,
∴⊙M与直线OB的位置关系是相是离.
故答案为相离.
【分析】作MH⊥OA于H,在Rt△OMH中,30度角所对的直角边等于斜边的一半可得MH=OM,把MH的值与半径2比较大小,根据直线与圆的位置关系,当圆心到直线的距离大于半径时,直线与圆相离可判断求解。
19.【答案】
30°
【解析】【解答】连接MO,作MD⊥OA,
∴AD=
OA=
,
MD=
=
,
∠MAO=30°,
又MA=OA,∴∠MOA=∠MAO=30°,
又OC是⊙M的切线,
∴∠MOC=90°,∠AOC=∠MOC+∠MCO=120°,
∴∠ACO=180°-∠AOC-∠MAO=180°-120°-30°=30°。
故答案为:30°。
【分析】由垂径定理和切线的性质可求出∠MAO和∠AOC的度数,再根据三角形内角和定理即可求出∠ACO的度数。
20.【答案】
50
【解析】【解答】∵PA、PB是⊙O的切线,
∴PA=PB,
∴∠PAB=∠PBA,
∵AC是⊙O的直径,PA是⊙O的切线,
∴AC⊥AP,
∴∠CAP=90°,
∵∠BAC=25°,
∴∠PBA=∠PAB=90°﹣25°=65°,
∴∠P=180°﹣∠PAB﹣∠PBA=180°﹣65°﹣65°=50°.
【分析】根据切线性质得出PA=PB,∠PAO=90°,求出∠PAB的度数,得出∠PAB=∠PBA,根据三角形的内角和定理求出即可.
21.【答案】
2.4<R≤3
【解析】【解答】解:如图,
∵BC>AC,
∴以C为圆心,R为半径所作的圆与斜边AB有两个交点,则圆的半径应大于CD,小于或等于AC,
由勾股定理知,AB=
?=5.
∵S△ABC=
?AC?BC=
?CD?AB=
×3×4=
×5?CD,
∴CD=2.4,
即R的取值范围是2.4<R≤3.
【分析】以C为圆心,R为半径所作的圆与斜边AB有两个交点,故AB与该圆相交,则圆的半径应大于CD,小于或等于AC,由勾股定理算出AB,根据三角形的面积法算出CD,从而得出答案。
22.【答案】
【解析】【解答】解:过点C作CP⊥直线AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.
直线AB的解析式为y=﹣
,即3x+4y﹣12=0,
∴CP=
=
.
∵PQ为⊙C的切线,
∴在Rt△CQP中,CQ=1,∠CQP=90°,
∴PQ=
=
.
故答案为:
.
【分析】过点C作CP⊥直线AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,由点到直线的距离求出CP的长度,再根据勾股定理即可求出PQ的长度.本题考查了切线的性质、点到直线的距离以及勾股定理,解题的关键是确定P、Q点的位置.本题属于中档题,难度不大,解决该题型题目时,借助于切线的性质寻找到PQ取最小值时点P、Q的位置是关键.
三、综合题
23.【答案】
(1)证明:∵AB=AC
∴∠ABC=∠ACB
∴∠CAB=180°-2∠ACB
∵BD⊥AC
∴∠BEC=90°,∠DBC+∠ACB=90°
∴∠DBC=90°-∠ACB
∵∠DAC=∠DBC=90°-∠ACB
∴2∠DAC=2(90°-∠ACB)=180°-2∠ACB
∴∠CAB=2∠DAC
(2)解:⊙O的直径CG,连结BG,
∵EF=EB,BD⊥AC
∴CF=CB
∴∠CFD=∠CBD,∠CAB=∠CDB=∠CFD+∠FCD=∠CBD+∠FCD
又由(1)可知∠CAB=2∠DAC=2∠CBD
∴∠FCD=∠CBD=∠CFD
∵CG为直径
∴∠CBG=90°
∴∠FCG=∠FCD+∠DCG=∠CBD+∠DBG=90°
∴FC⊥CG
∵CG为直径
∴FC为⊙O的切线
(3)解:∵AC=AB=10,BC=4
∴设
,
,
∴
,
∴AE=6,CE=4,BE=
8
∵∠CGB=∠EAB
∴sin∠CGB=
=sin∠EAB=
∴CG=
【解析】【分析】(1)根据切线的性质,可换算得出角度关系。
(2)根据切线的判定定理,可判定。
(3)利用勾股定理可解出直径。
24.【答案】
(1)解:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
∵OA=OC,
∴∠A=∠ACO,
∵∠A=∠1=∠2,
∴∠2=∠ACO,
∴∠2+∠BCO=90°,
∴∠PCO=90°,
∴OC⊥PC,
∴直线PC是⊙O的切线;
(2)解:∵∠ACB=90°,
∴∠A+∠ABC=90°
∴∠1=∠A,
∴∠1+∠ABC=90°,
∴∠CDB=90°,
∴CD2=AD?BD,
∵CD=4,BD=2,
∴AD=8,
∴AB=10,
∴OC=OB=5,
∵∠OCP=90°,CD⊥OP,
∴OC2=OD?OP,
∴52=(5﹣2)×OP,
∴OP=
,
∴PB=OP﹣OB=
.
【解析】【分析】(1)连接OC,由AB是⊙O的直径证得∠ACO+∠BCO=90°,由OA=OC证得∠2=∠A=∠ACO,由此得到∠PCO=90°,即证得直线PC是⊙O的切线;(2)利用∠1=∠A证得∠CDB=90°,得到CD2=AD?BD,求出AD,由此求得AB=10,OB=5;再由∠OCP=90°推出OC2=OD?OP,求出OP=
,由此求得线段BP的长.
25.【答案】
(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
(2)解:设该圆的半径为x.
在Rt△OAP中,∵∠P=30°,
∴PO=2OA=OD+PD,又∵OA=OD,
∴1+x=2x,解得:x=1
∴OA=PD=1,
所以⊙O的直径为2.
【解析】【分析】(1)连接OA,根据圆周角定理首先求得∠AOC的度数,然后根据等腰三角形的性质求得∠OAP=90°,从而求解;(2)根据直角三角形的性质,直角三角形中30°所对的边等于斜边的一半,即可求解.
(
2
)
(
1
)
同课章节目录
