人教版数学九年级上册 24.4弧长和扇形面积同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 24.4弧长和扇形面积同步测试试题(一)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 23:19:16 | ||
图片预览


文档简介
弧长和扇形面积同步测试试题(一)
一.选择题
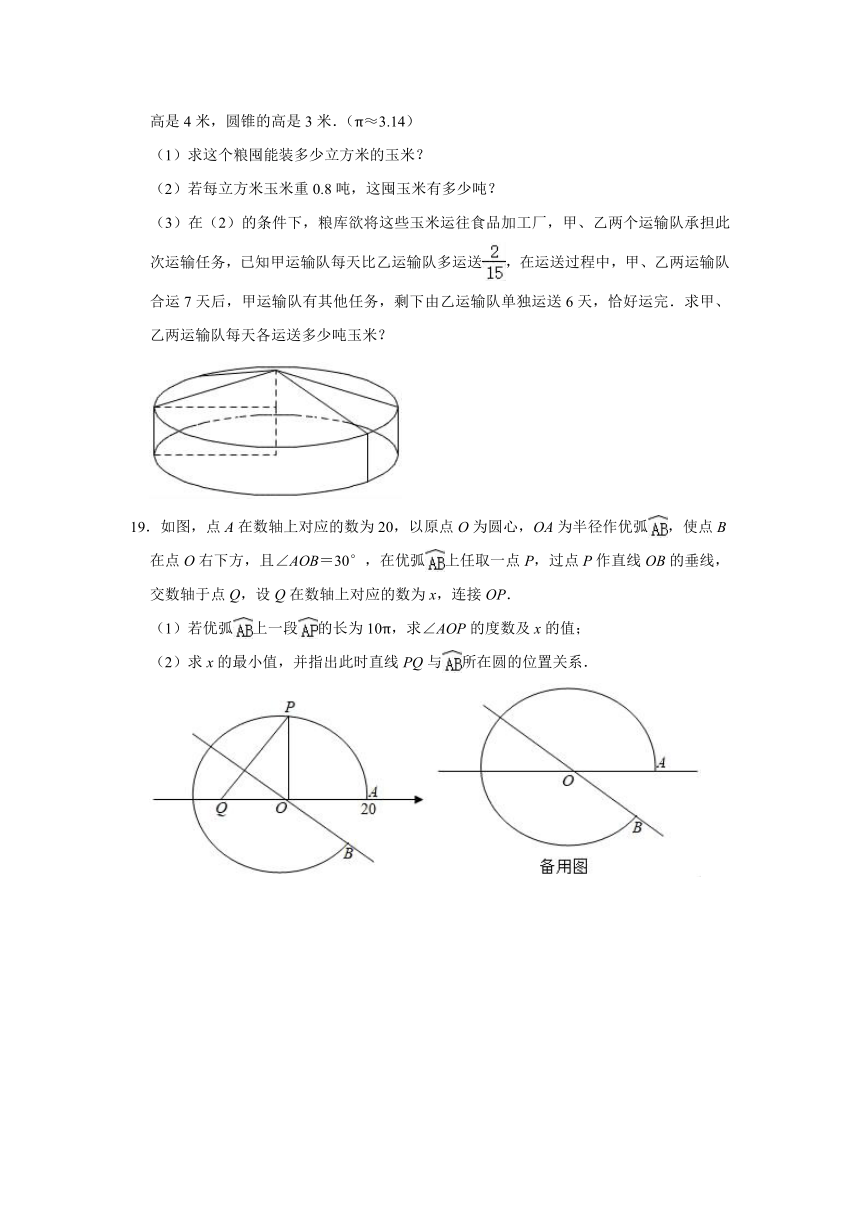
1.一个圆锥,底面半径是6厘米,高是10厘米,其体积是( )立方厘米.
A.360π B.120π C.90π D.30π
2.已知一扇形的半径等于圆的半径的2倍,且它的面积等于该已知圆的面积,则这一扇形的圆心角是( )度.
A.60 B.90 C.120 D.150
3.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.若圆弧的半径为3,所对的圆心角为60°,则弧长为( )
A.π B.π C.π D.3π
5.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2 B.100πcm2 C.100πcm2 D.50πcm2
6.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
7.如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,4)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为( )
A.8π B.π C.2π D.48π
8.如图,扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是( )
A. B. C. D.
9.将某圆锥形的冰淇淋纸套沿它的一条母线展开若不考虑接缝,它是一个半径为12cm,圆心角为120o的扇形,则( )
A.圆锥形冰淇淋纸套的底面半径为8cm
B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为
D.圆锥形冰淇淋纸套的高为
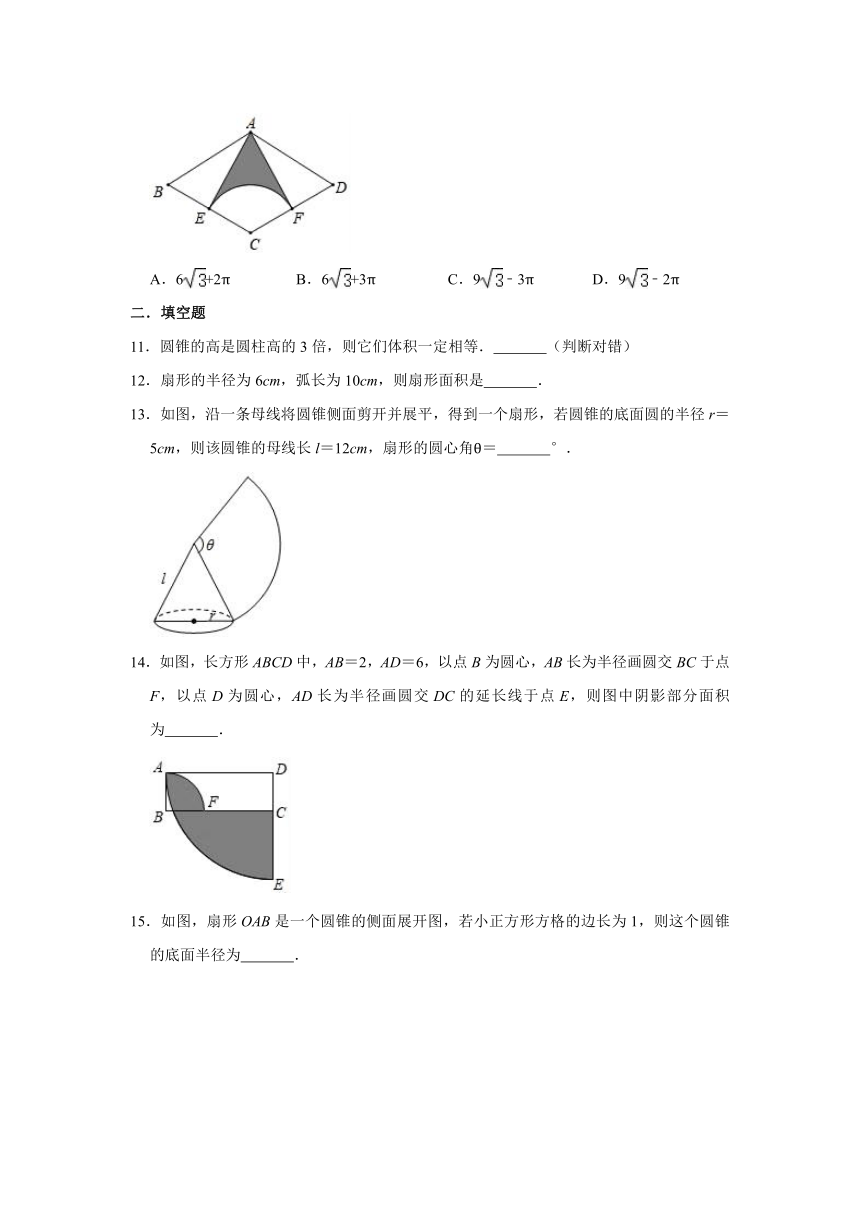
10.如图,在菱形ABCD中,点E是BC的中点,以C为圆心,CE长为半径作弧EF,交CD于点F,连接AE,AF.若AB=6,∠B=60°,则阴影部分的面积是( )
A.6+2π B.6+3π C.9﹣3π D.9﹣2π
二.填空题
11.圆锥的高是圆柱高的3倍,则它们体积一定相等. (判断对错)
12.扇形的半径为6cm,弧长为10cm,则扇形面积是 .
13.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=5cm,则该圆锥的母线长l=12cm,扇形的圆心角θ= °.
14.如图,长方形ABCD中,AB=2,AD=6,以点B为圆心,AB长为半径画圆交BC于点F,以点D为圆心,AD长为半径画圆交DC的延长线于点E,则图中阴影部分面积为 .
15.如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为 .
三.解答题
16.垃圾分类,从我做起.易拉罐是可回收垃圾,一吨易拉罐融化后能结成一吨很好的铝块,可少采20吨铝矿.生活中的易拉罐是一种类似于圆柱体的立体图形.
(1)圆柱体的侧面展开图是 (填“长方形”“圆”或“扇形”);
(2)圆柱体的铝制易拉罐上、下两个底面的半径都是4cm,侧面高为15cm,制作这样一个易拉罐需要面积多大的铝材?(不计接缝,结果保留π).
17.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过网格点A(0,8)、B(﹣8,8)、C(﹣12,4),请在网格图中进行如下操作:
(1)若该圆弧所在圆的圆心为D,则D点坐标为 ;
(2)连接AD、CD,则⊙D的半径长为 (结果保留根号).∠ADC的度数为 °;
(3)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长.(结果保留根号)
18.如图,一个装满玉米的粮囤,上面是圆锥形,下面是圆柱形,圆柱底面的半径是10米,高是4米,圆锥的高是3米.(π≈3.14)
(1)求这个粮囤能装多少立方米的玉米?
(2)若每立方米玉米重0.8吨,这囤玉米有多少吨?
(3)在(2)的条件下,粮库欲将这些玉米运往食品加工厂,甲、乙两个运输队承担此次运输任务,已知甲运输队每天比乙运输队多运送,在运送过程中,甲、乙两运输队合运7天后,甲运输队有其他任务,剩下由乙运输队单独运送6天,恰好运完.求甲、乙两运输队每天各运送多少吨玉米?
19.如图,点A在数轴上对应的数为20,以原点O为圆心,OA为半径作优弧,使点B在点O右下方,且∠AOB=30°,在优弧上任取一点P,过点P作直线OB的垂线,交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
(1)若优弧上一段的长为10π,求∠AOP的度数及x的值;
(2)求x的最小值,并指出此时直线PQ与所在圆的位置关系.
参考答案与试题解析
一.选择题
1.【解答】解:∵圆锥的底面半径是6厘米,高是10厘米,
∴圆锥的体积为V=sh=π×62×10=120π(立方厘米),
故选:B.
2.【解答】解:设圆的半径为r,
则扇形的半径为2r,
根据题意得:=πr2,
解得n=90.
故选:B.
3.【解答】解:①优弧比劣弧长,不一定,在同圆或等圆中结论成立,故①错误.
②三点可以确定一个圆,错误,应该是过不在同一直线上的三个点确定一个圆.故②错误.
③长度相等的弧是等弧,错误,长度相等的弧不一定相等,等弧的长度相等,故③错误.
④经过圆内的一个定点可以作无数条弦,故④正确.
故选:C.
4.【解答】解:弧长l==π,
故选:B.
5.【解答】解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
6.【解答】解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
7.【解答】解:过O′作O′M⊥OA于M,则∠O′MA=90°,
∵点O′的坐标是(4,4),
∴O′M=4,OM=4,
∵AO=8,
∴AM=8﹣4=4,
∴tan∠O′AM==,
∴∠O′AM=60°,
即旋转角为60°,
∴∠CAC′=∠OAO′=60°,
∵把△OAC绕点A按顺时针方向旋转到△O′AC′,
∴S△OAC=S△O′AC′,
∴阴影部分的面积S=S扇形OAO′+S△O′AC′﹣S△OAC﹣S扇形CAC′=S扇形OAO′﹣S扇形CAC′=﹣=8π,
故选:A.
8.【解答】解:连接OD,
∵点D是点O关于AC的对称点,
∴AD=OA,
∵OA=OD,
∴OA=OD=AD,
∴△OAD为等边三角形,
∴∠AOD=60°,
∴∠BOD=100°﹣60°=40°,
∴的长==π,
故选:B.
9.【解答】解:半径为12cm,圆心角为120°的扇形弧长是:(cm)
设圆锥的底面半径是r(cm)
则:2πr=8π,解得:r=4
即个圆淋的底面半径是4cm;
圆锥形冰淇淋纸套的高为=8(cm).
故选:C.
10.【解答】解:连接AC,
∵四边形ABCD是菱形,
∴AB=BC=6,
∵∠B=60°,E为BC的中点,
∴CE=BE=3=CF,△ABC是等边三角形,AB∥CD,
∵∠B=60°,
∴∠BCD=180°﹣∠B=120°,
由勾股定理得:AE==3,
∴S△AEB=S△AEC=×6×3×==S△AFC,
∴阴影部分的面积S=S△AEC+S△AFC﹣S扇形CEF=+﹣=9﹣3π,
故选:C.
二.填空题
11.【解答】解:当圆锥的底面积与圆柱的底面积不相等,则圆锥的高是圆柱高的3倍,则它们体积不相等.
故答案为错.
12.【解答】解:根据题意得,S扇形=lR==30(cm2).
故答案为30cm2.
13.【解答】解:根据题意得=2π5,
解得θ=150.
故答案为150.
14.【解答】解:在长方形ABCD中,∠B=∠D=90°,AB=2,AD=6,
阴影部分的面积=S扇形AED+S扇形AFB﹣S长方形ABCD=+﹣2×6=8π﹣12.
故答案为:8π﹣12.
15.【解答】解:根据勾股定理得,OA=OB==5,AB==5,
∴OA2+OB2=AB2,
∴△AOB为直角三角形,
∴∠AOB=90°,
设这个圆锥的底面半径为r,
根据题意得2πr=,解得r=,
即这个圆锥的底面半径为.
故答案为.
三.解答题(共4小题)
16.【解答】解:(1)圆柱体的侧面展开图是长方形,
故答案为:长方形;
(2)π×42×2+2π×4×15
=π×16×2+8π×15
=32π+120π
=152π(cm2),
即制作这样一个易拉罐需要面积152πcm2的铝材.
17.【解答】解:(1)点D的坐标为(﹣4,0);
(2)如图,AD==4,
即⊙D的半径长为4;
∵AD=CD=4,AC==4,
∴AD2+DC2=AC2,
∴△ACD为直角三角形,∠ADC的度数为90°;
故答案为(﹣4,0);4;90;
(3)设该圆锥的底面圆的半径长为r,
根据题意得2πr=,解得r=,
即该圆锥的底面圆的半径长为.
18.【解答】解:(1)
=3.14×
=1570(立方米)
答:这个粮囤能装1570立方米的玉米;
(2)0.8×1570=1256(吨).
答:这囤玉米有1256吨;
(3)设乙运输队每天运送x吨玉米,则甲运输队每天运送吨玉米.根据题意得,
,
解得x=60,
(吨).
答:乙运输队每天运送60吨玉米,甲运输队每天运送68吨玉米.
19.【解答】解:(1)如图1,
由=10π,
解得n=90°,
∴∠POQ=90°,
∴∠AOP=180°﹣∠POQ=90°,
∵PQ⊥OB,
∴∠PQO=60°,
∴tan∠PQO==,
∴OQ=
∴x=﹣;
(2)如备用图,当直线PQ与所在圆的位置关系相切时,x有最小值,
则∠QPO=90°
一.选择题
1.一个圆锥,底面半径是6厘米,高是10厘米,其体积是( )立方厘米.
A.360π B.120π C.90π D.30π
2.已知一扇形的半径等于圆的半径的2倍,且它的面积等于该已知圆的面积,则这一扇形的圆心角是( )度.
A.60 B.90 C.120 D.150
3.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.若圆弧的半径为3,所对的圆心角为60°,则弧长为( )
A.π B.π C.π D.3π
5.如图,从一块半径为20cm的圆形铁皮上剪出一个圆心角是60°的扇形ABC,则此扇形围成的圆锥的侧面积为( )
A.200πcm2 B.100πcm2 C.100πcm2 D.50πcm2
6.计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
若圆半径为1,当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.d(25%)=1
B.当x>50%时,d(x)>1
C.当x1>x2时,d(x1)>d(x2)
D.当x1+x2=100%时,d(x1)=d(x2)
7.如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,4)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为( )
A.8π B.π C.2π D.48π
8.如图,扇形OAB中,OB=3,∠AOB=100°,点C在OB上,连接AC,点O关于AC的对称点D刚好落在上,则的长是( )
A. B. C. D.
9.将某圆锥形的冰淇淋纸套沿它的一条母线展开若不考虑接缝,它是一个半径为12cm,圆心角为120o的扇形,则( )
A.圆锥形冰淇淋纸套的底面半径为8cm
B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为
D.圆锥形冰淇淋纸套的高为
10.如图,在菱形ABCD中,点E是BC的中点,以C为圆心,CE长为半径作弧EF,交CD于点F,连接AE,AF.若AB=6,∠B=60°,则阴影部分的面积是( )
A.6+2π B.6+3π C.9﹣3π D.9﹣2π
二.填空题
11.圆锥的高是圆柱高的3倍,则它们体积一定相等. (判断对错)
12.扇形的半径为6cm,弧长为10cm,则扇形面积是 .
13.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=5cm,则该圆锥的母线长l=12cm,扇形的圆心角θ= °.
14.如图,长方形ABCD中,AB=2,AD=6,以点B为圆心,AB长为半径画圆交BC于点F,以点D为圆心,AD长为半径画圆交DC的延长线于点E,则图中阴影部分面积为 .
15.如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为 .
三.解答题
16.垃圾分类,从我做起.易拉罐是可回收垃圾,一吨易拉罐融化后能结成一吨很好的铝块,可少采20吨铝矿.生活中的易拉罐是一种类似于圆柱体的立体图形.
(1)圆柱体的侧面展开图是 (填“长方形”“圆”或“扇形”);
(2)圆柱体的铝制易拉罐上、下两个底面的半径都是4cm,侧面高为15cm,制作这样一个易拉罐需要面积多大的铝材?(不计接缝,结果保留π).
17.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过网格点A(0,8)、B(﹣8,8)、C(﹣12,4),请在网格图中进行如下操作:
(1)若该圆弧所在圆的圆心为D,则D点坐标为 ;
(2)连接AD、CD,则⊙D的半径长为 (结果保留根号).∠ADC的度数为 °;
(3)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长.(结果保留根号)
18.如图,一个装满玉米的粮囤,上面是圆锥形,下面是圆柱形,圆柱底面的半径是10米,高是4米,圆锥的高是3米.(π≈3.14)
(1)求这个粮囤能装多少立方米的玉米?
(2)若每立方米玉米重0.8吨,这囤玉米有多少吨?
(3)在(2)的条件下,粮库欲将这些玉米运往食品加工厂,甲、乙两个运输队承担此次运输任务,已知甲运输队每天比乙运输队多运送,在运送过程中,甲、乙两运输队合运7天后,甲运输队有其他任务,剩下由乙运输队单独运送6天,恰好运完.求甲、乙两运输队每天各运送多少吨玉米?
19.如图,点A在数轴上对应的数为20,以原点O为圆心,OA为半径作优弧,使点B在点O右下方,且∠AOB=30°,在优弧上任取一点P,过点P作直线OB的垂线,交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
(1)若优弧上一段的长为10π,求∠AOP的度数及x的值;
(2)求x的最小值,并指出此时直线PQ与所在圆的位置关系.
参考答案与试题解析
一.选择题
1.【解答】解:∵圆锥的底面半径是6厘米,高是10厘米,
∴圆锥的体积为V=sh=π×62×10=120π(立方厘米),
故选:B.
2.【解答】解:设圆的半径为r,
则扇形的半径为2r,
根据题意得:=πr2,
解得n=90.
故选:B.
3.【解答】解:①优弧比劣弧长,不一定,在同圆或等圆中结论成立,故①错误.
②三点可以确定一个圆,错误,应该是过不在同一直线上的三个点确定一个圆.故②错误.
③长度相等的弧是等弧,错误,长度相等的弧不一定相等,等弧的长度相等,故③错误.
④经过圆内的一个定点可以作无数条弦,故④正确.
故选:C.
4.【解答】解:弧长l==π,
故选:B.
5.【解答】解:作OD⊥AB于D,如图,则AD=BD,
∵∠OAD=∠BAC=30°,
∴OD=OA=10,AD=OD=10,
∴AB=2AD=20,
∴扇形围成的圆锥的侧面积==200π(cm2).
故选:A.
6.【解答】解:A、d(25%)=>1,本选项不符合题意.
B、当x>50%时,0≤d(x)<2,本选项不符合题意.
C、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
D、当x1+x2=100%时,d(x1)=d(x2),本选项符合题意.
故选:D.
7.【解答】解:过O′作O′M⊥OA于M,则∠O′MA=90°,
∵点O′的坐标是(4,4),
∴O′M=4,OM=4,
∵AO=8,
∴AM=8﹣4=4,
∴tan∠O′AM==,
∴∠O′AM=60°,
即旋转角为60°,
∴∠CAC′=∠OAO′=60°,
∵把△OAC绕点A按顺时针方向旋转到△O′AC′,
∴S△OAC=S△O′AC′,
∴阴影部分的面积S=S扇形OAO′+S△O′AC′﹣S△OAC﹣S扇形CAC′=S扇形OAO′﹣S扇形CAC′=﹣=8π,
故选:A.
8.【解答】解:连接OD,
∵点D是点O关于AC的对称点,
∴AD=OA,
∵OA=OD,
∴OA=OD=AD,
∴△OAD为等边三角形,
∴∠AOD=60°,
∴∠BOD=100°﹣60°=40°,
∴的长==π,
故选:B.
9.【解答】解:半径为12cm,圆心角为120°的扇形弧长是:(cm)
设圆锥的底面半径是r(cm)
则:2πr=8π,解得:r=4
即个圆淋的底面半径是4cm;
圆锥形冰淇淋纸套的高为=8(cm).
故选:C.
10.【解答】解:连接AC,
∵四边形ABCD是菱形,
∴AB=BC=6,
∵∠B=60°,E为BC的中点,
∴CE=BE=3=CF,△ABC是等边三角形,AB∥CD,
∵∠B=60°,
∴∠BCD=180°﹣∠B=120°,
由勾股定理得:AE==3,
∴S△AEB=S△AEC=×6×3×==S△AFC,
∴阴影部分的面积S=S△AEC+S△AFC﹣S扇形CEF=+﹣=9﹣3π,
故选:C.
二.填空题
11.【解答】解:当圆锥的底面积与圆柱的底面积不相等,则圆锥的高是圆柱高的3倍,则它们体积不相等.
故答案为错.
12.【解答】解:根据题意得,S扇形=lR==30(cm2).
故答案为30cm2.
13.【解答】解:根据题意得=2π5,
解得θ=150.
故答案为150.
14.【解答】解:在长方形ABCD中,∠B=∠D=90°,AB=2,AD=6,
阴影部分的面积=S扇形AED+S扇形AFB﹣S长方形ABCD=+﹣2×6=8π﹣12.
故答案为:8π﹣12.
15.【解答】解:根据勾股定理得,OA=OB==5,AB==5,
∴OA2+OB2=AB2,
∴△AOB为直角三角形,
∴∠AOB=90°,
设这个圆锥的底面半径为r,
根据题意得2πr=,解得r=,
即这个圆锥的底面半径为.
故答案为.
三.解答题(共4小题)
16.【解答】解:(1)圆柱体的侧面展开图是长方形,
故答案为:长方形;
(2)π×42×2+2π×4×15
=π×16×2+8π×15
=32π+120π
=152π(cm2),
即制作这样一个易拉罐需要面积152πcm2的铝材.
17.【解答】解:(1)点D的坐标为(﹣4,0);
(2)如图,AD==4,
即⊙D的半径长为4;
∵AD=CD=4,AC==4,
∴AD2+DC2=AC2,
∴△ACD为直角三角形,∠ADC的度数为90°;
故答案为(﹣4,0);4;90;
(3)设该圆锥的底面圆的半径长为r,
根据题意得2πr=,解得r=,
即该圆锥的底面圆的半径长为.
18.【解答】解:(1)
=3.14×
=1570(立方米)
答:这个粮囤能装1570立方米的玉米;
(2)0.8×1570=1256(吨).
答:这囤玉米有1256吨;
(3)设乙运输队每天运送x吨玉米,则甲运输队每天运送吨玉米.根据题意得,
,
解得x=60,
(吨).
答:乙运输队每天运送60吨玉米,甲运输队每天运送68吨玉米.
19.【解答】解:(1)如图1,
由=10π,
解得n=90°,
∴∠POQ=90°,
∴∠AOP=180°﹣∠POQ=90°,
∵PQ⊥OB,
∴∠PQO=60°,
∴tan∠PQO==,
∴OQ=
∴x=﹣;
(2)如备用图,当直线PQ与所在圆的位置关系相切时,x有最小值,
则∠QPO=90°
同课章节目录
