人教版数学九年级上册 23.2中心对称同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 23.2中心对称同步测试试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 23:21:46 | ||
图片预览

文档简介
中心对称同步测试试题(一)
一.选择题
1.下列图形,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.在等边三角形,圆,菱形,正方形,正五边形,正六边形中是中心对称的图形有( )
A.3个 B.4个 C.5个 D.6个
3.在平面直角坐标系中,点(2,0)关于原点对称的点的坐标为( )
A.(-2,0) B(0,-2) C.(0,2) D(1,2)
4.下列汽车标志中,是中心对称图形的是( )
A. B.
C. D.
5.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B′的坐标为( )
A.(﹣,) B.(﹣1,) C.(﹣,) D.(﹣,)
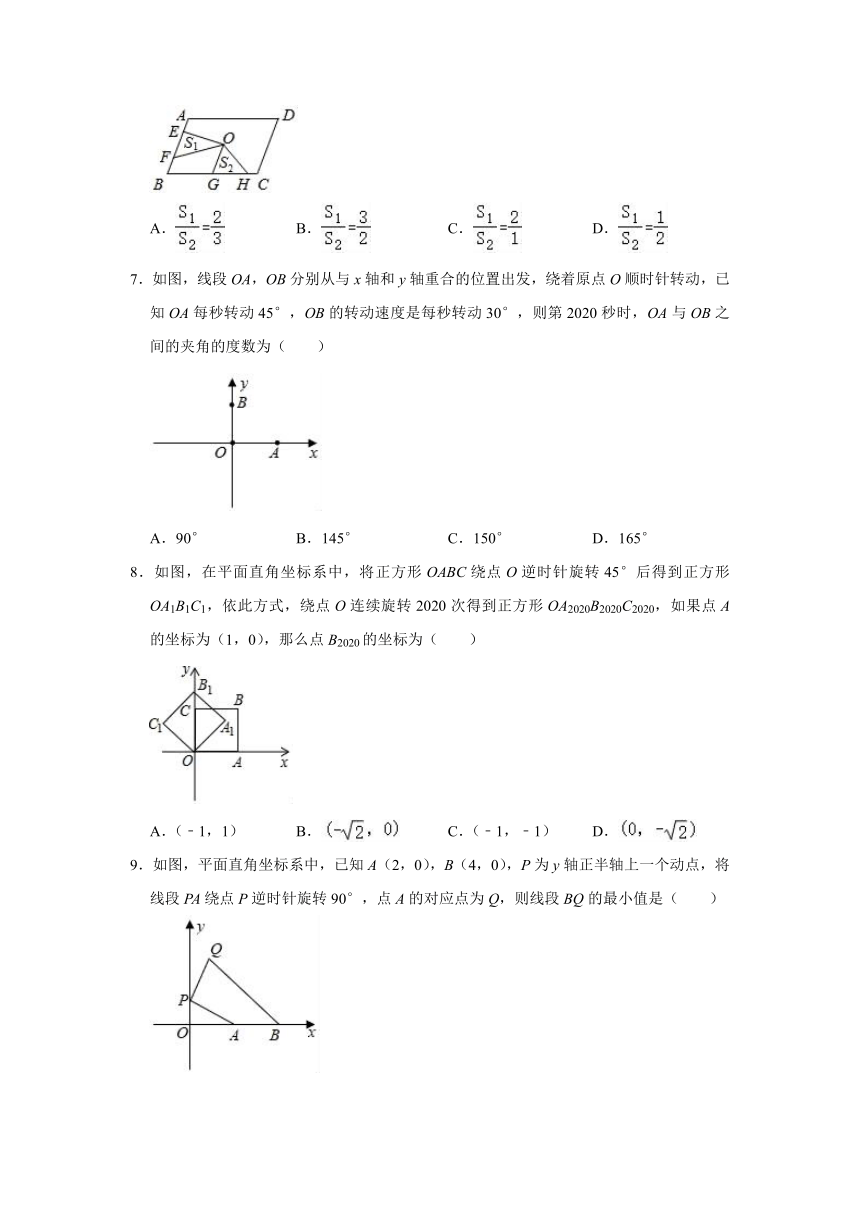
6.如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是( )
A. B. C. D.
7.如图,线段OA,OB分别从与x轴和y轴重合的位置出发,绕着原点O顺时针转动,已知OA每秒转动45°,OB的转动速度是每秒转动30°,则第2020秒时,OA与OB之间的夹角的度数为( )
A.90° B.145° C.150° D.165°
8.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2020次得到正方形OA2020B2020C2020,如果点A的坐标为(1,0),那么点B2020的坐标为( )
A.(﹣1,1) B. C.(﹣1,﹣1) D.
9.如图,平面直角坐标系中,已知A(2,0),B(4,0),P为y轴正半轴上一个动点,将线段PA绕点P逆时针旋转90°,点A的对应点为Q,则线段BQ的最小值是( )
A.3 B.5 C. D.2
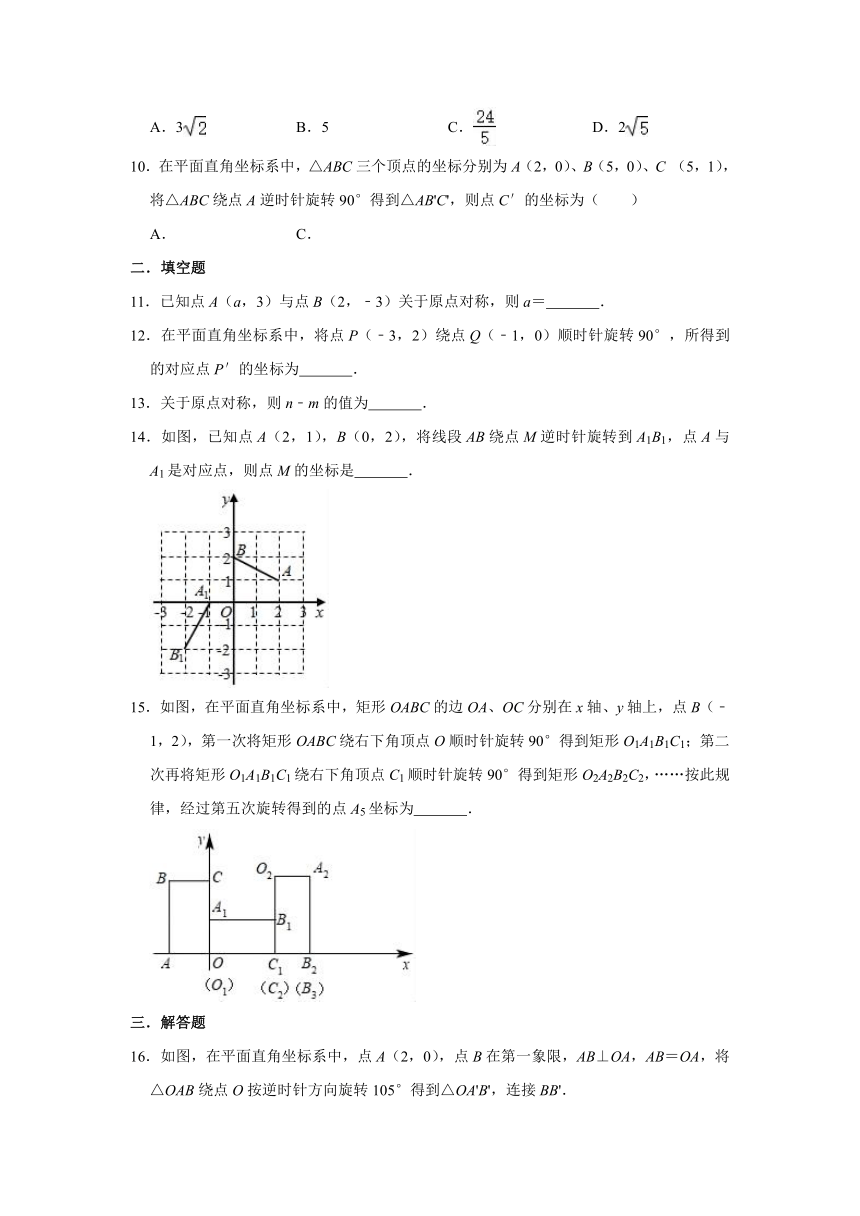
10.在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,0)、B(5,0)、C (5,1),将△ABC绕点A逆时针旋转90°得到△AB'C',则点C′的坐标为( )
A. C.
二.填空题
11.已知点A(a,3)与点B(2,﹣3)关于原点对称,则a= .
12.在平面直角坐标系中,将点P(﹣3,2)绕点Q(﹣1,0)顺时针旋转90°,所得到的对应点P′的坐标为 .
13.关于原点对称,则n﹣m的值为 .
14.如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1,点A与A1是对应点,则点M的坐标是 .
15.如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B(﹣1,2),第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1;第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,……按此规律,经过第五次旋转得到的点A5坐标为 .
三.解答题
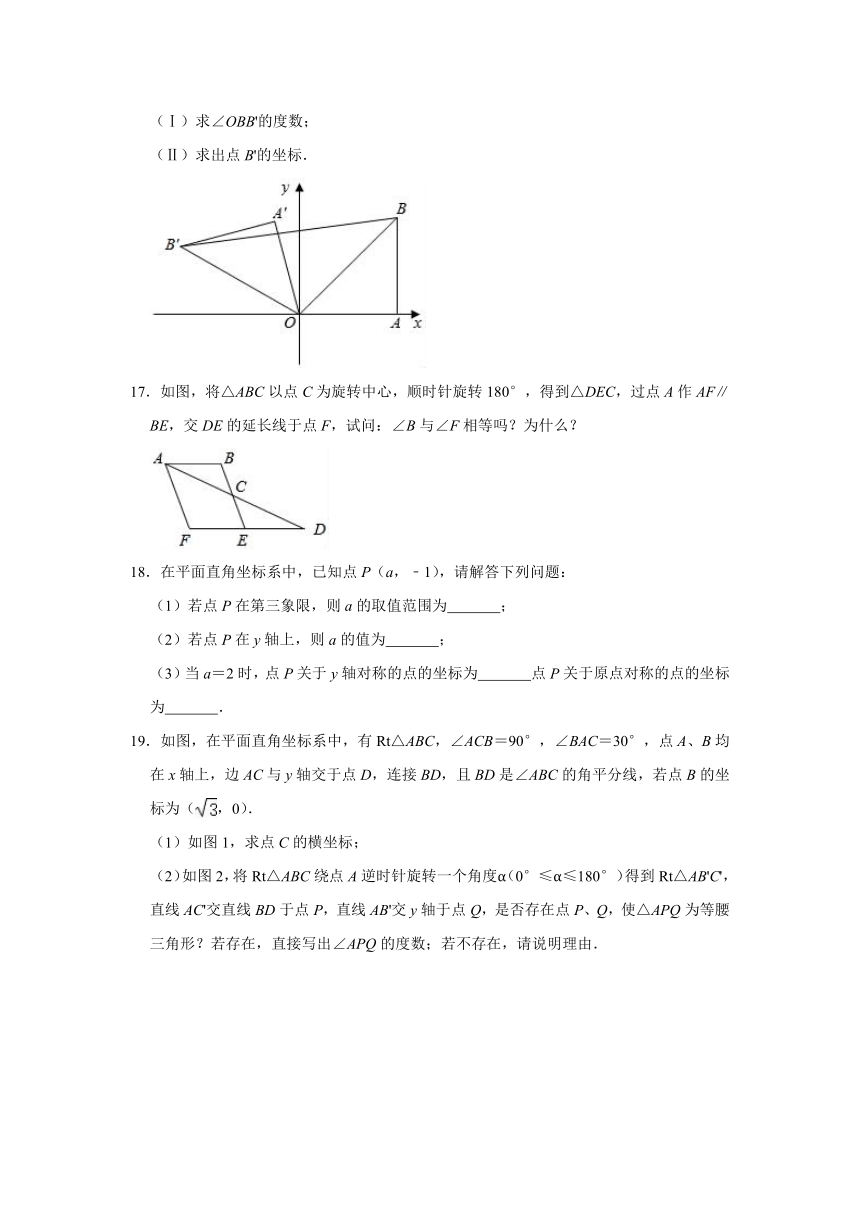
16.如图,在平面直角坐标系中,点A(2,0),点B在第一象限,AB⊥OA,AB=OA,将△OAB绕点O按逆时针方向旋转105°得到△OA'B',连接BB'.
(Ⅰ)求∠OBB'的度数;
(Ⅱ)求出点B'的坐标.
17.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
18.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:
(1)若点P在第三象限,则a的取值范围为 ;
(2)若点P在y轴上,则a的值为 ;
(3)当a=2时,点P关于y轴对称的点的坐标为 点P关于原点对称的点的坐标为 .
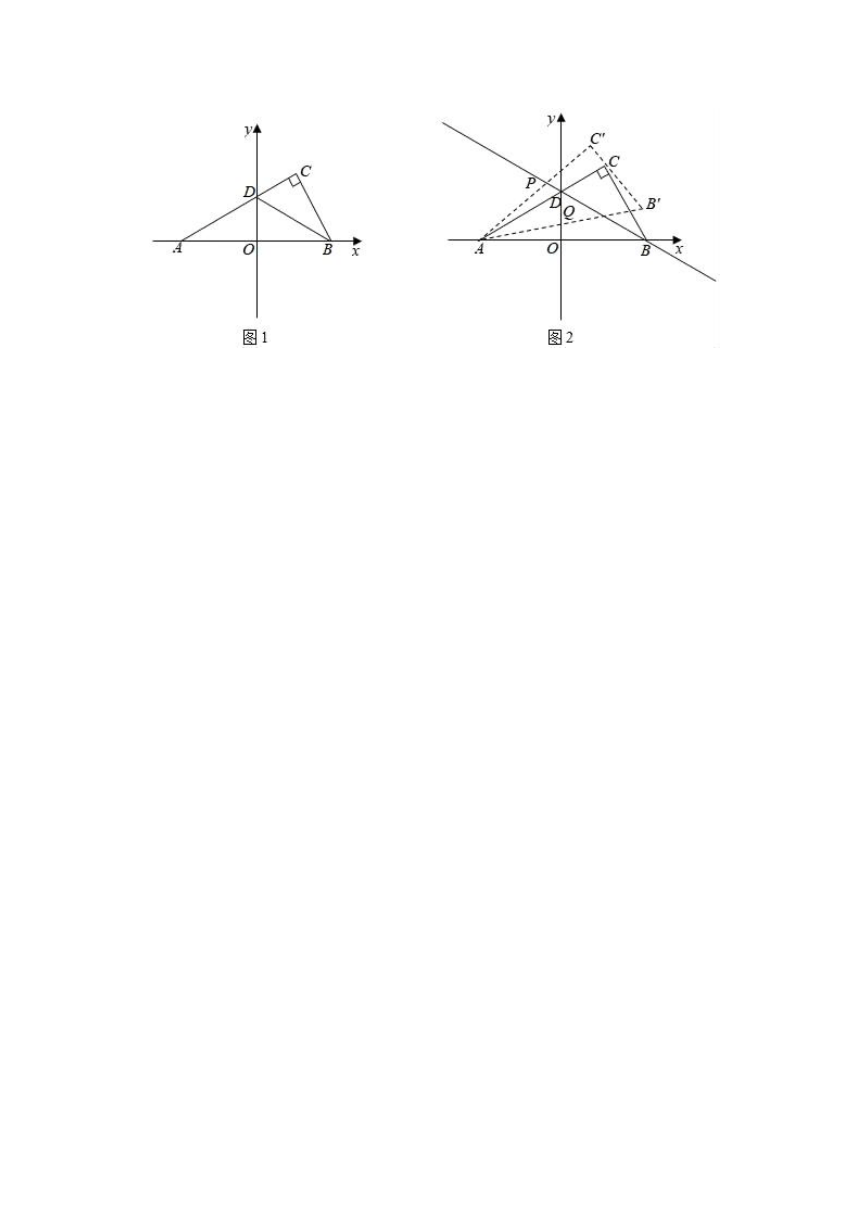
19.如图,在平面直角坐标系中,有Rt△ABC,∠ACB=90°,∠BAC=30°,点A、B均在x轴上,边AC与y轴交于点D,连接BD,且BD是∠ABC的角平分线,若点B的坐标为(,0).
(1)如图1,求点C的横坐标;
(2)如图2,将Rt△ABC绕点A逆时针旋转一个角度α(0°≤α≤180°)得到Rt△AB'C',直线AC'交直线BD于点P,直线AB'交y轴于点Q,是否存在点P、Q,使△APQ为等腰三角形?若存在,直接写出∠APQ的度数;若不存在,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A.是轴对称图形,不是中心对称图形,故此选项不符合题意;
B.不是轴对称图形,是中心对称图形,故此选项不符合题意;
C.既是中心对称图形,又是轴对称图形,故此选项符合题意;
D.是轴对称图形,不是中心对称图形,故此选项不符合题意;
故选:C.
2.【解答】解:在等边三角形,圆,菱形,正方形,正五边形,正六边形中是中心对称的图形有圆,菱形,正方形,正六边形共4个.
故选:B.
3.【解答】解:点(2,0)关于原点对称的点的坐标为(﹣2,0).
故选:A.
4.【解答】解:A、不是中心对称图形,故本选项不合题意;
B、不是中心对称图形,故本选项不合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不合题意;
故选:C.
5.【解答】解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.
∵A(1,0),
∴OA=1,
∵△AOB是等边三角形,BH⊥OA,
∴OH=AH=OA=,BH=OH=,
∴B(,),
∵∠AOB=∠BOB′=60°,∠JOA=90°,
∴∠BOJ=∠JOB′=30°,
∵OB=OB′,
∴BB′⊥OJ,
∴BJ=JB′,
∴B,B′关于y轴对称,
∴B′(﹣,),
故选:A.
6.【解答】解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,GH=BC,
∴S1=s,S2=s,
∴==,
故选:B.
7.【解答】解:设t秒第一次相遇.
由题意:270+30t=45t,
解得t=18,
相遇后设m秒第二次相遇,则有45t﹣30t=360,
解得t=24,
以后每过24秒相遇一次,
(2020﹣18)÷24=83…10,
∴2020秒时,10×45°﹣10×30°=150°,
故选:C.
8.【解答】解:∵四边形OABC是正方形,且OA=1,
∴B(1,1),
连接OB,
由勾股定理得:OB=,
由旋转得:OB=OB1=OB2=OB3=…=,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴B1(0,),B2(﹣1,1),B3(﹣,0),B(﹣1,﹣1),…,
发现是8次一循环,所以2020÷8=252…4,
∴点B2020的坐标为(﹣1,﹣1)
故选:C.
9.【解答】解:∵A(2,0),
∴OA=2,
设P(0,m),则OP=m,
作QM⊥y轴于M,
∵∠APQ=90°,
∴∠OAP+∠APO=∠APO+∠QPM,
∴∠OAP=∠QPM,
∵∠AOP=∠PMQ=90°,PA=PQ,
∴△AOP≌△PMQ(AAS),
∴MQ=OP=m,PM=OA=2,
∴Q(m,m+2),
∵B(4,0),
∴BQ==,
∴当m=1时,BQ有最小值3,
故选:A.
10.【解答】解:∵△ABC三个顶点的坐标分别为A(2,0)、B(5,0)、C (5,1),
将△ABC绕点A逆时针旋转90°得到△AB'C',如图所示:
则点C′的坐标为(1,3).
故选:B.
二.填空题
11.【解答】解:∵点A(a,3)与点B(2,﹣3)关于原点对称,
∴a=﹣2,
故答案为:﹣2.
12.【解答】解:如图,观察图象可知,P′(1,2).
故答案为(1,2).
13.【解答】解:∵点(m,3n)与点(﹣4,9)关于原点对称,
∴3n=﹣9,m=4,
∴n=﹣3,
∴n﹣m=﹣3﹣4=﹣7.
故答案为:﹣7.
14.【解答】解:如图,旋转中心M即为所求.M(1,﹣1).
故答案为(1,﹣1).
15.【解答】解:∵点B(﹣1,2),
∴A(﹣1,0),OA=BC=1,AB=OC=2,
∵第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1,且A1O=AO=1,OC1=OC=2,
第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,且B2O=C1O+B1C1=3…,依此规律,
∴A1(0,1),A2(3,2),A3(5,0),A4(6,1),A5(9,2),
故答案为(9,2).
三.解答题(共4小题)
16.【解答】解:(Ⅰ)∵△OAB≌△OA′B′,
∴OB=OB′,
又∠BOB′=105°,
∴∠OBB′=∠OB′B=(180°﹣105°)=37.5°.
(Ⅱ)过点B′作B′C垂直于x轴,垂足为C.
∵OA=AB=2,∠OAB=90°,
∴∠AOB=45°,OB=OA=2,
∴∠COB′=180°﹣105°﹣45°=30°,
在Rt△OCB′中,B′C=OB′=,
∴OC=CB′=,
∴B′(﹣,).
17.【解答】解:∠B与∠F相等,理由如下:
∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,
∴∠B=∠DEC,
∵AF∥BE,
∴∠F=∠DEC,
∴∠B=∠F.
18.【解答】解:(1)∵点P(a,﹣1),点P在第三象限,
∴a<0;
故答案为:a<0;
(2)∵点P(a,﹣1),点P在y轴上,
∴a=0;
故答案为:0;
(3)当a=2时,点P(a,﹣1)的坐标为:(2,﹣1)关于y轴对称的点的坐标为:(﹣2,﹣1),
点P关于原点对称的点的坐标为:(﹣2,1).
故答案为:(﹣2,﹣1),(﹣2,1).
19.【解答】解:(1)如图1中,过点C作CH⊥AB于H.
∵∠ABC=90°,∠CAB=30°,
∴∠ABC=90°﹣30°=60°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=30°,
∴∠DAB=∠DBA=30°,
∴DA=DB,
∵DO⊥AB,
∴OA=OB,
∵B(,0),
∴OA=OB=,
∴AB=2,
∴BC=AB=,
∵CH⊥AB,
∴∠CHB=90°,
∴BH=BC=,CH=BH=,
∴OH=OB﹣BH=,
∴C(,).
(2)如图2中,∵△PAQ是是等腰三角形,∠PAQ=30°
一.选择题
1.下列图形,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.在等边三角形,圆,菱形,正方形,正五边形,正六边形中是中心对称的图形有( )
A.3个 B.4个 C.5个 D.6个
3.在平面直角坐标系中,点(2,0)关于原点对称的点的坐标为( )
A.(-2,0) B(0,-2) C.(0,2) D(1,2)
4.下列汽车标志中,是中心对称图形的是( )
A. B.
C. D.
5.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B′的坐标为( )
A.(﹣,) B.(﹣1,) C.(﹣,) D.(﹣,)
6.如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是( )
A. B. C. D.
7.如图,线段OA,OB分别从与x轴和y轴重合的位置出发,绕着原点O顺时针转动,已知OA每秒转动45°,OB的转动速度是每秒转动30°,则第2020秒时,OA与OB之间的夹角的度数为( )
A.90° B.145° C.150° D.165°
8.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2020次得到正方形OA2020B2020C2020,如果点A的坐标为(1,0),那么点B2020的坐标为( )
A.(﹣1,1) B. C.(﹣1,﹣1) D.
9.如图,平面直角坐标系中,已知A(2,0),B(4,0),P为y轴正半轴上一个动点,将线段PA绕点P逆时针旋转90°,点A的对应点为Q,则线段BQ的最小值是( )
A.3 B.5 C. D.2
10.在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,0)、B(5,0)、C (5,1),将△ABC绕点A逆时针旋转90°得到△AB'C',则点C′的坐标为( )
A. C.
二.填空题
11.已知点A(a,3)与点B(2,﹣3)关于原点对称,则a= .
12.在平面直角坐标系中,将点P(﹣3,2)绕点Q(﹣1,0)顺时针旋转90°,所得到的对应点P′的坐标为 .
13.关于原点对称,则n﹣m的值为 .
14.如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1,点A与A1是对应点,则点M的坐标是 .
15.如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴上,点B(﹣1,2),第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1;第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,……按此规律,经过第五次旋转得到的点A5坐标为 .
三.解答题
16.如图,在平面直角坐标系中,点A(2,0),点B在第一象限,AB⊥OA,AB=OA,将△OAB绕点O按逆时针方向旋转105°得到△OA'B',连接BB'.
(Ⅰ)求∠OBB'的度数;
(Ⅱ)求出点B'的坐标.
17.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
18.在平面直角坐标系中,已知点P(a,﹣1),请解答下列问题:
(1)若点P在第三象限,则a的取值范围为 ;
(2)若点P在y轴上,则a的值为 ;
(3)当a=2时,点P关于y轴对称的点的坐标为 点P关于原点对称的点的坐标为 .
19.如图,在平面直角坐标系中,有Rt△ABC,∠ACB=90°,∠BAC=30°,点A、B均在x轴上,边AC与y轴交于点D,连接BD,且BD是∠ABC的角平分线,若点B的坐标为(,0).
(1)如图1,求点C的横坐标;
(2)如图2,将Rt△ABC绕点A逆时针旋转一个角度α(0°≤α≤180°)得到Rt△AB'C',直线AC'交直线BD于点P,直线AB'交y轴于点Q,是否存在点P、Q,使△APQ为等腰三角形?若存在,直接写出∠APQ的度数;若不存在,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A.是轴对称图形,不是中心对称图形,故此选项不符合题意;
B.不是轴对称图形,是中心对称图形,故此选项不符合题意;
C.既是中心对称图形,又是轴对称图形,故此选项符合题意;
D.是轴对称图形,不是中心对称图形,故此选项不符合题意;
故选:C.
2.【解答】解:在等边三角形,圆,菱形,正方形,正五边形,正六边形中是中心对称的图形有圆,菱形,正方形,正六边形共4个.
故选:B.
3.【解答】解:点(2,0)关于原点对称的点的坐标为(﹣2,0).
故选:A.
4.【解答】解:A、不是中心对称图形,故本选项不合题意;
B、不是中心对称图形,故本选项不合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不合题意;
故选:C.
5.【解答】解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.
∵A(1,0),
∴OA=1,
∵△AOB是等边三角形,BH⊥OA,
∴OH=AH=OA=,BH=OH=,
∴B(,),
∵∠AOB=∠BOB′=60°,∠JOA=90°,
∴∠BOJ=∠JOB′=30°,
∵OB=OB′,
∴BB′⊥OJ,
∴BJ=JB′,
∴B,B′关于y轴对称,
∴B′(﹣,),
故选:A.
6.【解答】解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,GH=BC,
∴S1=s,S2=s,
∴==,
故选:B.
7.【解答】解:设t秒第一次相遇.
由题意:270+30t=45t,
解得t=18,
相遇后设m秒第二次相遇,则有45t﹣30t=360,
解得t=24,
以后每过24秒相遇一次,
(2020﹣18)÷24=83…10,
∴2020秒时,10×45°﹣10×30°=150°,
故选:C.
8.【解答】解:∵四边形OABC是正方形,且OA=1,
∴B(1,1),
连接OB,
由勾股定理得:OB=,
由旋转得:OB=OB1=OB2=OB3=…=,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴B1(0,),B2(﹣1,1),B3(﹣,0),B(﹣1,﹣1),…,
发现是8次一循环,所以2020÷8=252…4,
∴点B2020的坐标为(﹣1,﹣1)
故选:C.
9.【解答】解:∵A(2,0),
∴OA=2,
设P(0,m),则OP=m,
作QM⊥y轴于M,
∵∠APQ=90°,
∴∠OAP+∠APO=∠APO+∠QPM,
∴∠OAP=∠QPM,
∵∠AOP=∠PMQ=90°,PA=PQ,
∴△AOP≌△PMQ(AAS),
∴MQ=OP=m,PM=OA=2,
∴Q(m,m+2),
∵B(4,0),
∴BQ==,
∴当m=1时,BQ有最小值3,
故选:A.
10.【解答】解:∵△ABC三个顶点的坐标分别为A(2,0)、B(5,0)、C (5,1),
将△ABC绕点A逆时针旋转90°得到△AB'C',如图所示:
则点C′的坐标为(1,3).
故选:B.
二.填空题
11.【解答】解:∵点A(a,3)与点B(2,﹣3)关于原点对称,
∴a=﹣2,
故答案为:﹣2.
12.【解答】解:如图,观察图象可知,P′(1,2).
故答案为(1,2).
13.【解答】解:∵点(m,3n)与点(﹣4,9)关于原点对称,
∴3n=﹣9,m=4,
∴n=﹣3,
∴n﹣m=﹣3﹣4=﹣7.
故答案为:﹣7.
14.【解答】解:如图,旋转中心M即为所求.M(1,﹣1).
故答案为(1,﹣1).
15.【解答】解:∵点B(﹣1,2),
∴A(﹣1,0),OA=BC=1,AB=OC=2,
∵第一次将矩形OABC绕右下角顶点O顺时针旋转90°得到矩形O1A1B1C1,且A1O=AO=1,OC1=OC=2,
第二次再将矩形O1A1B1C1绕右下角顶点C1顺时针旋转90°得到矩形O2A2B2C2,且B2O=C1O+B1C1=3…,依此规律,
∴A1(0,1),A2(3,2),A3(5,0),A4(6,1),A5(9,2),
故答案为(9,2).
三.解答题(共4小题)
16.【解答】解:(Ⅰ)∵△OAB≌△OA′B′,
∴OB=OB′,
又∠BOB′=105°,
∴∠OBB′=∠OB′B=(180°﹣105°)=37.5°.
(Ⅱ)过点B′作B′C垂直于x轴,垂足为C.
∵OA=AB=2,∠OAB=90°,
∴∠AOB=45°,OB=OA=2,
∴∠COB′=180°﹣105°﹣45°=30°,
在Rt△OCB′中,B′C=OB′=,
∴OC=CB′=,
∴B′(﹣,).
17.【解答】解:∠B与∠F相等,理由如下:
∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,
∴∠B=∠DEC,
∵AF∥BE,
∴∠F=∠DEC,
∴∠B=∠F.
18.【解答】解:(1)∵点P(a,﹣1),点P在第三象限,
∴a<0;
故答案为:a<0;
(2)∵点P(a,﹣1),点P在y轴上,
∴a=0;
故答案为:0;
(3)当a=2时,点P(a,﹣1)的坐标为:(2,﹣1)关于y轴对称的点的坐标为:(﹣2,﹣1),
点P关于原点对称的点的坐标为:(﹣2,1).
故答案为:(﹣2,﹣1),(﹣2,1).
19.【解答】解:(1)如图1中,过点C作CH⊥AB于H.
∵∠ABC=90°,∠CAB=30°,
∴∠ABC=90°﹣30°=60°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=30°,
∴∠DAB=∠DBA=30°,
∴DA=DB,
∵DO⊥AB,
∴OA=OB,
∵B(,0),
∴OA=OB=,
∴AB=2,
∴BC=AB=,
∵CH⊥AB,
∴∠CHB=90°,
∴BH=BC=,CH=BH=,
∴OH=OB﹣BH=,
∴C(,).
(2)如图2中,∵△PAQ是是等腰三角形,∠PAQ=30°
同课章节目录
