人教版数学七年级上册 第4章4.1--4.3达标检测题(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级上册 第4章4.1--4.3达标检测题(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 618.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 23:24:24 | ||
图片预览

文档简介
人教版七年级数学上册练习:4.1--4.3达标检测题含答案
4.1
几何图形
一、单选题
1.图是一座房子的平面图,组成这幅图的几何图形有( )
A.三角形、长方形
B.三角形、长方形、正方形
C.三角形、长方形、正方形、梯形
D.长方形、正方形、梯形
2.奥运会的标志是五环,这五环的每一个环的形状与下列图形中类似的是( )
A.三角形
B.正方形
C.圆
D.长方体
3.下列图形中,属于立体图形的是(
)
A.
B.
C.
D.
4.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线、面、体
C.角、三角形、正方形、圆
D.点、相交线、线段、长方体
5.下列物体中,最接近圆柱的是(
)
A.
B.
C.
D.
6.用平面截一个正方体,可能截出的边数最多的多边形是( )
A.七边形
B.六边形
C.五边形
D.四边形[]
7.如图,将下面的平面图形绕直线旋转一周,得到的立体图形是( )
A.
B.
C.
D.
8.
用一个平面去截下列立体图形,截面可以得到三角形的立体图形有( )
[]
A.1个
B.2个
C.3个
D.4个
9.下列现象,能说明“线动成面”的是( )
A.天空划过一道流星
B.汽车雨刷在挡风玻璃上刷出的痕迹
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
10.某校年级(1)班在“迎中考日誓师”活动中打算制作一个带有正方体挂坠的倒计时牌挂在班级,正方体的每个面上分别书写“成功舍我其谁”六个字如图是该班同学设计的正方体挂坠的平面展开图,那么“谁”对面的字是( )
A.成
B.功
C.其
D.我
二、填空题
11.下列几何体属于柱体的有____个.
12.如图,该图是一个正方体的展开图,把展开图折叠成正方体后,有“少”字一面的相对面上的字是____.
13.如图,将纸板四周突起部分折起,可制成高为a的长方体形状的无盖纸盒.若纸盒的容积为4a2b,底面长方形的一边长为b,则纸板的面积是________.
14.下列平面图形中,将编号为_____(只需填写编号)的平面图形绕轴旋转一周,可得到图中所示的立体图形.
三、解答题
15.说出下列图形的名称.
16.如图是一个正方体盒子的展开图,要把-8、10、-12、8、-10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.
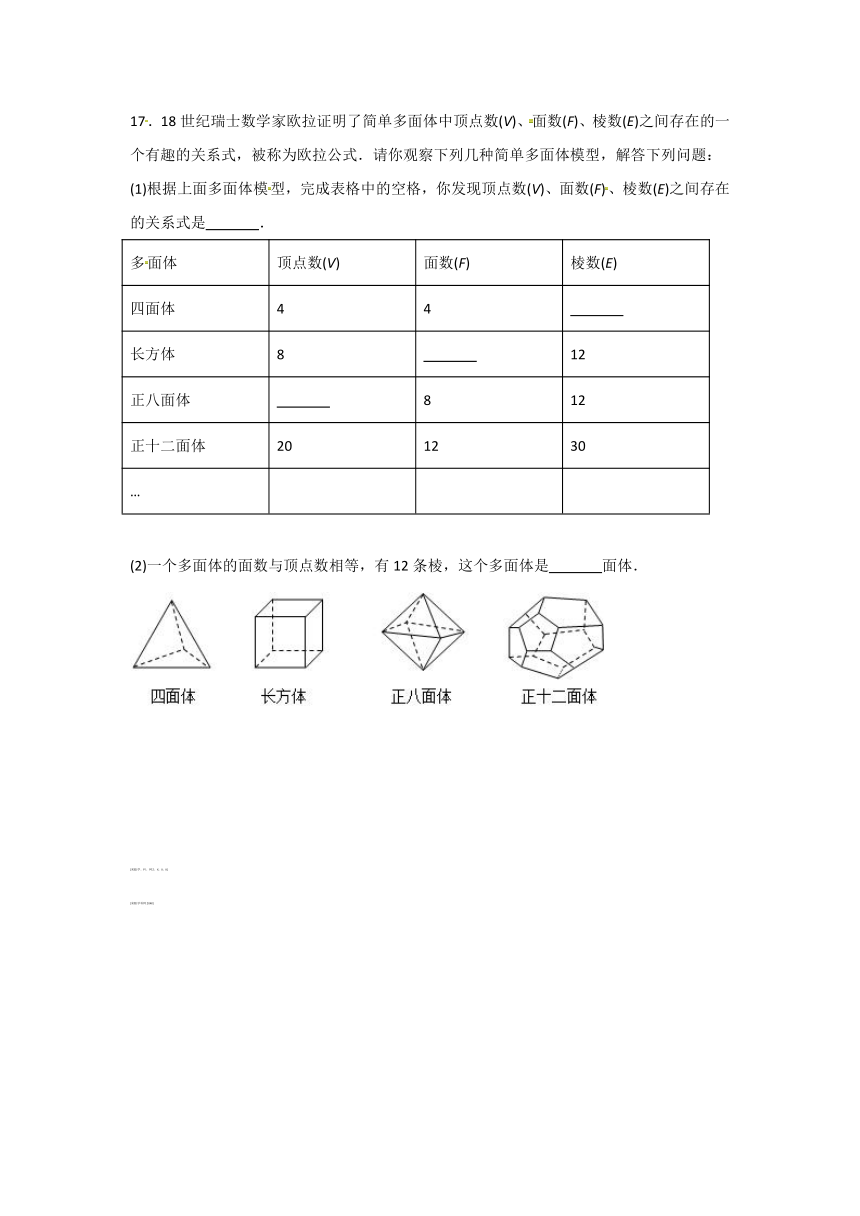
17.18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格,你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是
.
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
12
正八面体
8
12
正十二面体
20
12
30
…
(2)一个多面体的面数与顶点数相等,有12条棱,这个多面体是
面体.
[]
[]
18.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)
答案
1.C
2.C
3.C
4.C
5.C
6.B
7.D
8.C
9.B
10.D[]
11.5
12.梦.
13.8a2+6ab
14.②.
15.根据平面图形的定义可知:它们依次是圆、三角形、正方形、长方形、平行四边形、梯形、五边形、六边形.
16.解:
17.(1)四面体的棱数为6;
长方体的面数为6;
正八面体的顶点数为6;
关系式为:V+F﹣E=2;
(2)由题意得:F+F﹣12=2,
解得F=7.
故答案为:V+F﹣E=2;7.
18.(1)由图形可知:底面正方形的边长=18-12=6.包装盒的表面积=6×6×2+4×6×12=72+288=360(平方厘米).
答:制作一个这样的包装盒需要360平方厘米的硬纸板.
(2)10×360÷10000×5=1.8(元)
制作10个这的包装盒需花1.8元
4.2直线、射线、线段
一.选择题
1.平面上有不同的三个点,经过其中任意两点画直线,一共可以画( )
A.1条
B.2条
C.3条
D.1条或3条
2.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3
B.1.5
C.1.2
D.1
3.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
4.下列四个生产生活现象,可以用公理“两点之间,线段最短”来解释的是( )
A.用两个钉子可以把木条钉在墙上
B.植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上
C.打靶的时候,眼睛要与枪上的准星、靶心在同一直线上
D.为了缩短航程把弯曲的河道改直
5.如图,线段AB=18cm,点M为线段AB的中点,点C将线段MB分成MC:CB=1:2,则线段AC的长度为( )
A.6cm
B.12cm
C.9cm
D.15cm
6.已知线段AB=8cm,AC=6cm,下面有四个说法:
①线段BC长可能为2cm;②线段BC长可能为14cm;
③线段BC长不可能为5cm;④线段BC长可能为9cm.
所有正确说法的序号是( )
A.①②
B.③④
C.①②④
D.①②③④
7.线段AB=9,点C在线段AB上,且有AC=AB,M是AB的中点,则MC等于( )
A.3
B.
C.
D.
8.如图,马聪同学用剪刀沿虚线将片平整的银杏叶剪掉一部分,发现剩下的叶片的周长比原叶片的周长要小,能正确解释这一现象的数学知识是( )
A.两点确定一条直线
B.经过一点有无数条
直线
C.两点之间线段最短
D.两直线相交只有一个交点
9.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.线段的定义
D.圆弧的定义
10.在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有( )
A.①③
B.②③
C.③④
D.②④
二.填空题
11.两地之间弯曲的道路改直,可以缩短路程,其根据的数学道理是
.
12.如图,已知线段AB=8cm,M是AB的中点,P是线段MB上一点,N为PB的中点,NB=1.5cm,则线段MP=
cm.
13.如图,AE⊥AB于A点,DB⊥AB于B点,点P为线段AB上任意一点,若AE=2,DB=4,AB=8,则PE+PD的最小值是
.
14.海南环岛高铁是世界首创,其中某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票
种,票价
种.
15.曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好的观赏风光,如图,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是
.
三.解答题
16.如图,点B,D都在线段AC上,AB=12,点D是线段AB的中点,BD=3BC,求AC的长.
17.如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
18.如图,已知C,D是线段AB上的两个点,M,N分别为AC,BD的中点.
(1)若AB=10,CD=4,求AC+BD的长及MN的长;
(2)如果AB=2a+3b,CD=b,用含a,b的式子表示MN的长.
19.已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧.
(1)若AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式=,则=
.
参考答案与试题解析
一.选择题
1.【解答】解:如图,经过其中任意两点画直线可以画3条直线或1条直线,
故选:D.
2.【解答】解:∵点C是AB的中点,AB=9,
∴AC=CB=AB=4.5,
当点D是AB的三等分点,点D在线段BC上时,BD=AB=3,
∴CD=4.5﹣3=1.5,
当点D是AB的三等分点,点D′在线段AC上时,AD′=AB=3,
∴CD′=4.5﹣3=1.5,
故选:B.
3.【解答】解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
4.【解答】解:A、根据两点确定一条直线,故本选项不符合题意;
B、确定树之间的距离,即得到相互的坐标关系,故本选项不符合题意;
C、根据两点确定一条直线,故本选项不符合题意;
D、根据两点之间,线段最短,故本选项符合题意.
故选:D.
5.【解答】解:∵线段AB=18cm,点M为线段AB的中点,
∴AM=BM=AB=9,
∵点C将线段MB分成MC:CB=1:2,
设MC=x,CB=2x,
∴BM=MC+CB=3x,
∴3x=9,解得x=3,
∴AC=AM+MC=9+3=12.
则线段AC的长度为12.
故选:B.
6.【解答】解:∵线段AB=8cm,AC=6cm,
∴如图1,当A,B,C在一条直线上,
∴BC=AB﹣AC=8﹣6=2(cm),故①正确;
如图2,当A,B,C在一条直线上,
∴BC=AB+AC=8+6=14(cm),故②正确;
如图3,当A,B,C不在一条直线上,
8﹣6<BC<8+6,
故线段BC可能为5或9,故③错误,④正确.
故选:C.
7.【解答】解:∵AB=9,
∴AC=AB=3,
∵M是AB的中点,
∴AM=AB=
∴MC=AM﹣AC=﹣3=
故选:B.
8.【解答】解:马聪同学用剪刀沿虚线将片平整的银杏叶剪掉一部分,发现剩下的叶片的周长比原叶片的周长要小,能正确解释这一现象的数学知识是:两点之间线段最短.
故选:C.
9.【解答】解:剩下的银杏叶的周长比原银杏叶的周长要小根据是两点之间线段最短,
故选:A.
10.【解答】解:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,运用的数学依据是:两点确定一条直线;
②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,运用的数学依据是:两点确定一条直线;
③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程,运用的数学依据是:两点之间,线段最短,符合题意;
④从A地到B地架设电线,总是尽可能沿着线段AB架设,运用的数学依据是:两点之间,线段最短,符合题意.
故选:C.
二.填空题
11.【解答】解:将弯曲的公路改直,可以缩短路程,这是根据两点之间,线段最短.
故答案为:两点之间,线段最短.
12.【解答】解:∵M是AB的中点,AB=8cm,
∴AM=BM=4cm,
∵N为PB的中点,NB=1.5cm,
∴PB=2NB=3cm,
∴MP=BM﹣PB=4﹣3=1cm.
故答案为1.
13.【解答】解:过点D作DT⊥EA交EA的延长线于T,连接DE.
∵AE⊥AB,DB⊥AB,DT⊥ET,
∴∠B=∠T=∠BAT=90°,
∴四边形ABDT是矩形,
∴BD=AT=4,AB=DT=8,
∴ET=AE+AT=2+4=6,
∴DE===10,
∵PE+PD≥DE,
∴PE+PD≥10,
∴PE+PD的最小值为10.
故答案为10.
14.【解答】解:令6个站分别为A、B、C、D、E、F,
则可得所组成的线段有15条,即需要安排15×2=30种不同的车票.
故答案为:30、15.
15.【解答】解:其中蕴含的数学道理是两点之间线段最短,
故答案为:两点之间线段最短.
三.解答题(共4小题)
16.【解答】解:∵AB=12,点D是线段AB的中点,
∴BD=12÷2=6;
∵BD=3BC,
∴BC=6÷3=2,
∴AC=AB+BC=12+2=14.
17.【解答】解:(1)①∵AB=CD,
∴AB+BC=CD+BC,
即,AC=BD,
故答案为:=;
②∵BC=AC,且AC=12cm,
∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),
∴AD=AC+CD=12+3=15(cm),
故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,
∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
18.【解答】解:(1)∵AB=10,CD=4,
∴AC+BD=AB﹣CD=10﹣4=6,
∵M、N分别为AC、BD的中点,
∴AM+BN=AC+BD=(AC+BD)=3,
∴MN=AB﹣(AM+BN)=10﹣3=7;
(2)根据(1)的结论,
AM+BN=AC+BD=(AC+BD)=(2a+3b﹣b)=a+b,
∴MN=AB﹣(AM+BN)=2a+3b﹣(a+b)=a+2b.
19.【解答】解:(1)AC=2BC,AB=18,DE=8,
∴BC=6,AC=12,
①如图,
∵E为BC中点,
∴CE=3,
∴CD=5,
∴AD=AB﹣DB=18﹣11=7;
②如图,
Ⅰ、当点E在点F的左侧,
∵CE+EF=3,BC=6,
∴点F是BC的中点,
∴CF=BF=3,
∴AF=AB﹣BF=18﹣3=15,
∴AD=AF=5;
Ⅱ、当点E在点F的右侧,
∵AC=12,CE+EF=CF=3,
∴AF=AC﹣CF=9,
∴AF=3AD=9,
∴AD=3.
综上所述:AD的长为3或5;
(2)∵AC=2BC,AB=2DE,满足关系式=,
Ⅰ、当点E在点C右侧时,如图,
设CE=x,DC=y,
则DE=x+y,
∴AB=2(x+y)
AC=AB=(x+y)
∴AD=AC﹣DC=x+y
BC=AB=(x+y)
∴BE=BC﹣CE=y﹣x
∴AD+EC=x+y
∵2(AD+EC)=3BE
∴2(x+y)=3(y﹣x)
解得,17x=4y,
∴===.
Ⅱ、当点E在点A左侧时,如图,
设CE=x,DC=y,
则DE=y﹣x,
∴AB=2(y﹣x)
AC=AB=(y﹣x)
∴AD=DC﹣AC=x﹣y
BC=AB=(y﹣x)
∴BE=BC+CE=y+x
∴AD+EC=x﹣y
∵2(AD+EC)=3B
4.3角
一.选择题
1.若把钟面上的每个刻度均看作一个点,那么表示2时的刻度在表示12时的刻度的方向为( )
A.北偏东60°
B.北偏东30°
C.南偏东60°
D.南偏东30°
2.若∠A与∠B互为补角,则∠A+∠B=( )
A.60°
B.90°
C.120°
D.180°
3.如图,轮船航行到B处观测小岛A的方向是北偏西32°,那么小岛A观测到轮船B的方向是( )
A.南偏西32°
B.南偏东32°
C.南偏西58°
D.南偏东58°
4.如图,将一副三角板重叠放在一起,使直角顶点重合于点O.若∠AOC=130°,则∠BOD=( )
A.30°
B.40°
C.50°
D.60°
5.如果乙船在甲船的南偏东30°方向,那么甲船在乙船的( )方向.
A.北偏东30°
B.北偏西30°
C.北偏东60°
D.北偏西60°
6.下列说法中,错误的是( )
A.两点之间的线段最短
B.如果∠α=53°38′,那么∠α余角的度数为36°22′
C.一个锐角的余角比这个角的补角小
D.互补的两个角一个是锐角一个是钝角
7.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对
B.4对
C.3对
D.2对
8.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
9.如图,用量角器度量∠AOB,可以读出∠AOB的度数为( )
A.30°
B.60°
C.120°
D.150°
10.为防止森林火灾的发生,会在森林中设置多个观测点,如图,若起火点M在观测台B的南偏东46°的方向上,点A表示另一处观测台,若AM⊥BM,那么起火点M在观测台A的( )
A.南偏东44°
B.南偏西44°
C.北偏东46°
D.北偏西46°
二.填空题
11.若两个角互补,且度数之比为3:2,求较大角度数为
.
12.计算:已知∠α=20°20′,则∠α的余角为
.
13.张雷同学从A地出发沿北偏东60°的方向行驶到B地,再由B地沿南偏西35°的方向行驶到C地,则∠ABC=
度.
14.如图,轮船A在岛屿B的北偏东45°方向和岛屿C的北偏东15°方向,则∠BAC=
°.
15.如图,已知点C在点A的北偏东19°,在点B的北偏西71°,若CB=9,AC=12,则AB=
.
三.解答题
16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD和∠AOC互余,并求∠COD的度数.
17.如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
18.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
19.如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠COE的度数.
小方同学的解答过程是这样的:
解:设∠COE=α.
由于已知∠BOE=2∠COE,
所以∠BOE=2α.
所以∠BOC=∠BOE+∠COE=2α+α=3α.
因为OC平分∠BOF,根据角平分线的定义,
所以∠BOC=∠FOC=3α.
因为∠EOF是直角,
所以∠EOF=90°.
所以∠EOF=∠FOC+∠COE=3α+α=4α=90°
所以α=22°50′
即∠COE=22°50′
以上的解答中有一处错误,导致了从这一步往后的错误.
这一处错误是:
.
应该修改为(从错误处开始):
.
参考答案与试题解析
一.选择题
1.【解答】解:表示2时的刻度在表示12时的刻度的方向为南偏东60°,
故选:C.
2.【解答】解:∵∠A与∠B互为补角,
∴∠A+∠B=180°.
故选:D.
3.【解答】解:由图可知,AB方向相反,从小岛A同时观测轮船B的方向是南偏东32°,
故选:B.
4.【解答】解:∵∠AOC=130°,
∴∠BOC=∠AOC﹣∠AOB=40°,
∴∠BOD=∠COD﹣∠BOC=50°.
故选:C.
5.【解答】解:如图:
∵从甲船看乙船,乙船在甲船的南偏东30°方向,
∴从乙船看甲船,甲船在乙船的北偏西30°方向.
故选:B.
6.【解答】解:A、两点之间的线段最短,是线段的性质,故本小题正确,不符合题意;
B、如果∠α=53°38′,那么∠α余角的度数为90°﹣53°38′=36°22′,故本小题正确,不符合题意;
C、一个锐角α的余角是90°﹣α,这个角的补角是180°﹣α,(180°﹣α)﹣(90°﹣α)=90°,正确,不符合题意;
D、两个直角也是互补的角,故本小题错误,符合题意.
故选:D.
7.【解答】解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠1=∠AOC,
∠2=∠BOD,
∠AOE=∠COD,
∠BOE=∠COD,
∴图中相等的角有5对.
故选:A.
8.【解答】解:∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
9.【解答】解:看内圈的数字可得:∠AOB=120°,
故选:C.
10.【解答】解:如图:
因为AM⊥BM,
所以∠2+∠3=90°,
因为南北方向的直线平行,
所以∠2=46°,∠1=∠3,
所以∠3=90°﹣∠2=90°﹣46°=44°,
所以∠1=44°,
所以起火点M在观测台A的南偏西44°,
故选:B.
二.填空题
11.【解答】解:因为两个角的度数之比为3:2,
所以设这两个角的度数分别为(3x)°和(2x)°.
根据题意,列方程,得3x+2x=180,
解这个方程,得x=36,
所以3x=108.
即较大角度数为108°.
故答案为108°.
12.【解答】解:∠α的余角=90°﹣20°20′=69°40′.
故答案为:69°40′.
13.【解答】解:如图所示,
∵AD∥BE,∠1=60°,
∴∠ABE=∠DAB=60°,
又∵∠CBE=35°,
∴∠ABC=60°﹣35°=25°.
故答案为:25.
14.【解答】解:如图,
∵CE,DB是正北方向,
∴BD∥CE,
∵∠DBA=45°,
∴∠BFC=∠DBA=45°,
∵∠ACE=15°,
∴∠BAC=∠BFC﹣∠ACE=45°﹣15°=30°.
故答案为:30.
15.【解答】解:如图:
∵点C在点A的北偏东19°,在点B的北偏西71°,
∴∠ACD=19°,∠BCD=71°,
∴∠ACB=19°+71°=90°,
∴AC2+CB2=AB2,
∵CB=9,AC=12,
∴122+92=AB2,
∴AB=15,
故答案为:15.
三.解答题
16.【解答】解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.
∵∠AOB=128°,OC平分∠AOB,
∴∠AOC=∠AOB=64°,
∵∠COD和∠AOC互余,
∴∠COD=90°﹣∠AOC=26°.
17.【解答】解:如图,由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∴∠BAC=∠BAD+∠CAD=40°+15°=55°,
∴∠CBA=∠EBC﹣∠EBA=80°﹣40°=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC
=180°﹣55°﹣40°=85°,
答:从C岛看A,B两岛的视角∠ACB的度数为85°.
18.【解答】解:(1)因为点C为OP的中点,
所以OC=2km,
因为OA=2km,
所以可得出距小明家距离相同的是学校和公园;
(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.
19.【解答】解:如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠COE的度数.
小方同学的解答过程是这样的:
解:设∠COE=α,
由于已知∠BOE=2∠COE,
所以∠BOE=2α,
所以∠BOC=∠BOE+∠COE=2α+α=3α,
因为OC平分∠BOF,根据角平分线的定义,
所以∠BOC=∠FOC=3α,
因为∠EOF是直角,
所以∠EOF=90°,
所以∠EOF=∠FOC+∠COE=3α+α=4α=90°,
所以α=22.5°,
即∠COE=22.5°.
所以这一处错误是:α=22°50′.
应该修改为(从错误处开始):所以α=22.5°
4.1
几何图形
一、单选题
1.图是一座房子的平面图,组成这幅图的几何图形有( )
A.三角形、长方形
B.三角形、长方形、正方形
C.三角形、长方形、正方形、梯形
D.长方形、正方形、梯形
2.奥运会的标志是五环,这五环的每一个环的形状与下列图形中类似的是( )
A.三角形
B.正方形
C.圆
D.长方体
3.下列图形中,属于立体图形的是(
)
A.
B.
C.
D.
4.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线、面、体
C.角、三角形、正方形、圆
D.点、相交线、线段、长方体
5.下列物体中,最接近圆柱的是(
)
A.
B.
C.
D.
6.用平面截一个正方体,可能截出的边数最多的多边形是( )
A.七边形
B.六边形
C.五边形
D.四边形[]
7.如图,将下面的平面图形绕直线旋转一周,得到的立体图形是( )
A.
B.
C.
D.
8.
用一个平面去截下列立体图形,截面可以得到三角形的立体图形有( )
[]
A.1个
B.2个
C.3个
D.4个
9.下列现象,能说明“线动成面”的是( )
A.天空划过一道流星
B.汽车雨刷在挡风玻璃上刷出的痕迹
C.抛出一块小石子,石子在空中飞行的路线
D.旋转一扇门,门在空中运动的痕迹
10.某校年级(1)班在“迎中考日誓师”活动中打算制作一个带有正方体挂坠的倒计时牌挂在班级,正方体的每个面上分别书写“成功舍我其谁”六个字如图是该班同学设计的正方体挂坠的平面展开图,那么“谁”对面的字是( )
A.成
B.功
C.其
D.我
二、填空题
11.下列几何体属于柱体的有____个.
12.如图,该图是一个正方体的展开图,把展开图折叠成正方体后,有“少”字一面的相对面上的字是____.
13.如图,将纸板四周突起部分折起,可制成高为a的长方体形状的无盖纸盒.若纸盒的容积为4a2b,底面长方形的一边长为b,则纸板的面积是________.
14.下列平面图形中,将编号为_____(只需填写编号)的平面图形绕轴旋转一周,可得到图中所示的立体图形.
三、解答题
15.说出下列图形的名称.
16.如图是一个正方体盒子的展开图,要把-8、10、-12、8、-10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.
17.18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格,你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是
.
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
12
正八面体
8
12
正十二面体
20
12
30
…
(2)一个多面体的面数与顶点数相等,有12条棱,这个多面体是
面体.
[]
[]
18.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)
答案
1.C
2.C
3.C
4.C
5.C
6.B
7.D
8.C
9.B
10.D[]
11.5
12.梦.
13.8a2+6ab
14.②.
15.根据平面图形的定义可知:它们依次是圆、三角形、正方形、长方形、平行四边形、梯形、五边形、六边形.
16.解:
17.(1)四面体的棱数为6;
长方体的面数为6;
正八面体的顶点数为6;
关系式为:V+F﹣E=2;
(2)由题意得:F+F﹣12=2,
解得F=7.
故答案为:V+F﹣E=2;7.
18.(1)由图形可知:底面正方形的边长=18-12=6.包装盒的表面积=6×6×2+4×6×12=72+288=360(平方厘米).
答:制作一个这样的包装盒需要360平方厘米的硬纸板.
(2)10×360÷10000×5=1.8(元)
制作10个这的包装盒需花1.8元
4.2直线、射线、线段
一.选择题
1.平面上有不同的三个点,经过其中任意两点画直线,一共可以画( )
A.1条
B.2条
C.3条
D.1条或3条
2.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3
B.1.5
C.1.2
D.1
3.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
4.下列四个生产生活现象,可以用公理“两点之间,线段最短”来解释的是( )
A.用两个钉子可以把木条钉在墙上
B.植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上
C.打靶的时候,眼睛要与枪上的准星、靶心在同一直线上
D.为了缩短航程把弯曲的河道改直
5.如图,线段AB=18cm,点M为线段AB的中点,点C将线段MB分成MC:CB=1:2,则线段AC的长度为( )
A.6cm
B.12cm
C.9cm
D.15cm
6.已知线段AB=8cm,AC=6cm,下面有四个说法:
①线段BC长可能为2cm;②线段BC长可能为14cm;
③线段BC长不可能为5cm;④线段BC长可能为9cm.
所有正确说法的序号是( )
A.①②
B.③④
C.①②④
D.①②③④
7.线段AB=9,点C在线段AB上,且有AC=AB,M是AB的中点,则MC等于( )
A.3
B.
C.
D.
8.如图,马聪同学用剪刀沿虚线将片平整的银杏叶剪掉一部分,发现剩下的叶片的周长比原叶片的周长要小,能正确解释这一现象的数学知识是( )
A.两点确定一条直线
B.经过一点有无数条
直线
C.两点之间线段最短
D.两直线相交只有一个交点
9.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.线段的定义
D.圆弧的定义
10.在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有( )
A.①③
B.②③
C.③④
D.②④
二.填空题
11.两地之间弯曲的道路改直,可以缩短路程,其根据的数学道理是
.
12.如图,已知线段AB=8cm,M是AB的中点,P是线段MB上一点,N为PB的中点,NB=1.5cm,则线段MP=
cm.
13.如图,AE⊥AB于A点,DB⊥AB于B点,点P为线段AB上任意一点,若AE=2,DB=4,AB=8,则PE+PD的最小值是
.
14.海南环岛高铁是世界首创,其中某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票
种,票价
种.
15.曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好的观赏风光,如图,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是
.
三.解答题
16.如图,点B,D都在线段AC上,AB=12,点D是线段AB的中点,BD=3BC,求AC的长.
17.如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
18.如图,已知C,D是线段AB上的两个点,M,N分别为AC,BD的中点.
(1)若AB=10,CD=4,求AC+BD的长及MN的长;
(2)如果AB=2a+3b,CD=b,用含a,b的式子表示MN的长.
19.已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧.
(1)若AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式=,则=
.
参考答案与试题解析
一.选择题
1.【解答】解:如图,经过其中任意两点画直线可以画3条直线或1条直线,
故选:D.
2.【解答】解:∵点C是AB的中点,AB=9,
∴AC=CB=AB=4.5,
当点D是AB的三等分点,点D在线段BC上时,BD=AB=3,
∴CD=4.5﹣3=1.5,
当点D是AB的三等分点,点D′在线段AC上时,AD′=AB=3,
∴CD′=4.5﹣3=1.5,
故选:B.
3.【解答】解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
4.【解答】解:A、根据两点确定一条直线,故本选项不符合题意;
B、确定树之间的距离,即得到相互的坐标关系,故本选项不符合题意;
C、根据两点确定一条直线,故本选项不符合题意;
D、根据两点之间,线段最短,故本选项符合题意.
故选:D.
5.【解答】解:∵线段AB=18cm,点M为线段AB的中点,
∴AM=BM=AB=9,
∵点C将线段MB分成MC:CB=1:2,
设MC=x,CB=2x,
∴BM=MC+CB=3x,
∴3x=9,解得x=3,
∴AC=AM+MC=9+3=12.
则线段AC的长度为12.
故选:B.
6.【解答】解:∵线段AB=8cm,AC=6cm,
∴如图1,当A,B,C在一条直线上,
∴BC=AB﹣AC=8﹣6=2(cm),故①正确;
如图2,当A,B,C在一条直线上,
∴BC=AB+AC=8+6=14(cm),故②正确;
如图3,当A,B,C不在一条直线上,
8﹣6<BC<8+6,
故线段BC可能为5或9,故③错误,④正确.
故选:C.
7.【解答】解:∵AB=9,
∴AC=AB=3,
∵M是AB的中点,
∴AM=AB=
∴MC=AM﹣AC=﹣3=
故选:B.
8.【解答】解:马聪同学用剪刀沿虚线将片平整的银杏叶剪掉一部分,发现剩下的叶片的周长比原叶片的周长要小,能正确解释这一现象的数学知识是:两点之间线段最短.
故选:C.
9.【解答】解:剩下的银杏叶的周长比原银杏叶的周长要小根据是两点之间线段最短,
故选:A.
10.【解答】解:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,运用的数学依据是:两点确定一条直线;
②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,运用的数学依据是:两点确定一条直线;
③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程,运用的数学依据是:两点之间,线段最短,符合题意;
④从A地到B地架设电线,总是尽可能沿着线段AB架设,运用的数学依据是:两点之间,线段最短,符合题意.
故选:C.
二.填空题
11.【解答】解:将弯曲的公路改直,可以缩短路程,这是根据两点之间,线段最短.
故答案为:两点之间,线段最短.
12.【解答】解:∵M是AB的中点,AB=8cm,
∴AM=BM=4cm,
∵N为PB的中点,NB=1.5cm,
∴PB=2NB=3cm,
∴MP=BM﹣PB=4﹣3=1cm.
故答案为1.
13.【解答】解:过点D作DT⊥EA交EA的延长线于T,连接DE.
∵AE⊥AB,DB⊥AB,DT⊥ET,
∴∠B=∠T=∠BAT=90°,
∴四边形ABDT是矩形,
∴BD=AT=4,AB=DT=8,
∴ET=AE+AT=2+4=6,
∴DE===10,
∵PE+PD≥DE,
∴PE+PD≥10,
∴PE+PD的最小值为10.
故答案为10.
14.【解答】解:令6个站分别为A、B、C、D、E、F,
则可得所组成的线段有15条,即需要安排15×2=30种不同的车票.
故答案为:30、15.
15.【解答】解:其中蕴含的数学道理是两点之间线段最短,
故答案为:两点之间线段最短.
三.解答题(共4小题)
16.【解答】解:∵AB=12,点D是线段AB的中点,
∴BD=12÷2=6;
∵BD=3BC,
∴BC=6÷3=2,
∴AC=AB+BC=12+2=14.
17.【解答】解:(1)①∵AB=CD,
∴AB+BC=CD+BC,
即,AC=BD,
故答案为:=;
②∵BC=AC,且AC=12cm,
∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),
∴AD=AC+CD=12+3=15(cm),
故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,
∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
18.【解答】解:(1)∵AB=10,CD=4,
∴AC+BD=AB﹣CD=10﹣4=6,
∵M、N分别为AC、BD的中点,
∴AM+BN=AC+BD=(AC+BD)=3,
∴MN=AB﹣(AM+BN)=10﹣3=7;
(2)根据(1)的结论,
AM+BN=AC+BD=(AC+BD)=(2a+3b﹣b)=a+b,
∴MN=AB﹣(AM+BN)=2a+3b﹣(a+b)=a+2b.
19.【解答】解:(1)AC=2BC,AB=18,DE=8,
∴BC=6,AC=12,
①如图,
∵E为BC中点,
∴CE=3,
∴CD=5,
∴AD=AB﹣DB=18﹣11=7;
②如图,
Ⅰ、当点E在点F的左侧,
∵CE+EF=3,BC=6,
∴点F是BC的中点,
∴CF=BF=3,
∴AF=AB﹣BF=18﹣3=15,
∴AD=AF=5;
Ⅱ、当点E在点F的右侧,
∵AC=12,CE+EF=CF=3,
∴AF=AC﹣CF=9,
∴AF=3AD=9,
∴AD=3.
综上所述:AD的长为3或5;
(2)∵AC=2BC,AB=2DE,满足关系式=,
Ⅰ、当点E在点C右侧时,如图,
设CE=x,DC=y,
则DE=x+y,
∴AB=2(x+y)
AC=AB=(x+y)
∴AD=AC﹣DC=x+y
BC=AB=(x+y)
∴BE=BC﹣CE=y﹣x
∴AD+EC=x+y
∵2(AD+EC)=3BE
∴2(x+y)=3(y﹣x)
解得,17x=4y,
∴===.
Ⅱ、当点E在点A左侧时,如图,
设CE=x,DC=y,
则DE=y﹣x,
∴AB=2(y﹣x)
AC=AB=(y﹣x)
∴AD=DC﹣AC=x﹣y
BC=AB=(y﹣x)
∴BE=BC+CE=y+x
∴AD+EC=x﹣y
∵2(AD+EC)=3B
4.3角
一.选择题
1.若把钟面上的每个刻度均看作一个点,那么表示2时的刻度在表示12时的刻度的方向为( )
A.北偏东60°
B.北偏东30°
C.南偏东60°
D.南偏东30°
2.若∠A与∠B互为补角,则∠A+∠B=( )
A.60°
B.90°
C.120°
D.180°
3.如图,轮船航行到B处观测小岛A的方向是北偏西32°,那么小岛A观测到轮船B的方向是( )
A.南偏西32°
B.南偏东32°
C.南偏西58°
D.南偏东58°
4.如图,将一副三角板重叠放在一起,使直角顶点重合于点O.若∠AOC=130°,则∠BOD=( )
A.30°
B.40°
C.50°
D.60°
5.如果乙船在甲船的南偏东30°方向,那么甲船在乙船的( )方向.
A.北偏东30°
B.北偏西30°
C.北偏东60°
D.北偏西60°
6.下列说法中,错误的是( )
A.两点之间的线段最短
B.如果∠α=53°38′,那么∠α余角的度数为36°22′
C.一个锐角的余角比这个角的补角小
D.互补的两个角一个是锐角一个是钝角
7.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对
B.4对
C.3对
D.2对
8.按图1~图4的步骤作图,下列结论错误的是( )
A.∠AOB=∠AOP
B.∠AOP=∠BOP
C.2∠BOP=∠AOB
D.∠BOP=2∠AOP
9.如图,用量角器度量∠AOB,可以读出∠AOB的度数为( )
A.30°
B.60°
C.120°
D.150°
10.为防止森林火灾的发生,会在森林中设置多个观测点,如图,若起火点M在观测台B的南偏东46°的方向上,点A表示另一处观测台,若AM⊥BM,那么起火点M在观测台A的( )
A.南偏东44°
B.南偏西44°
C.北偏东46°
D.北偏西46°
二.填空题
11.若两个角互补,且度数之比为3:2,求较大角度数为
.
12.计算:已知∠α=20°20′,则∠α的余角为
.
13.张雷同学从A地出发沿北偏东60°的方向行驶到B地,再由B地沿南偏西35°的方向行驶到C地,则∠ABC=
度.
14.如图,轮船A在岛屿B的北偏东45°方向和岛屿C的北偏东15°方向,则∠BAC=
°.
15.如图,已知点C在点A的北偏东19°,在点B的北偏西71°,若CB=9,AC=12,则AB=
.
三.解答题
16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD和∠AOC互余,并求∠COD的度数.
17.如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
18.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中到小明家距离相同的是哪些地方?
(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
19.如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠COE的度数.
小方同学的解答过程是这样的:
解:设∠COE=α.
由于已知∠BOE=2∠COE,
所以∠BOE=2α.
所以∠BOC=∠BOE+∠COE=2α+α=3α.
因为OC平分∠BOF,根据角平分线的定义,
所以∠BOC=∠FOC=3α.
因为∠EOF是直角,
所以∠EOF=90°.
所以∠EOF=∠FOC+∠COE=3α+α=4α=90°
所以α=22°50′
即∠COE=22°50′
以上的解答中有一处错误,导致了从这一步往后的错误.
这一处错误是:
.
应该修改为(从错误处开始):
.
参考答案与试题解析
一.选择题
1.【解答】解:表示2时的刻度在表示12时的刻度的方向为南偏东60°,
故选:C.
2.【解答】解:∵∠A与∠B互为补角,
∴∠A+∠B=180°.
故选:D.
3.【解答】解:由图可知,AB方向相反,从小岛A同时观测轮船B的方向是南偏东32°,
故选:B.
4.【解答】解:∵∠AOC=130°,
∴∠BOC=∠AOC﹣∠AOB=40°,
∴∠BOD=∠COD﹣∠BOC=50°.
故选:C.
5.【解答】解:如图:
∵从甲船看乙船,乙船在甲船的南偏东30°方向,
∴从乙船看甲船,甲船在乙船的北偏西30°方向.
故选:B.
6.【解答】解:A、两点之间的线段最短,是线段的性质,故本小题正确,不符合题意;
B、如果∠α=53°38′,那么∠α余角的度数为90°﹣53°38′=36°22′,故本小题正确,不符合题意;
C、一个锐角α的余角是90°﹣α,这个角的补角是180°﹣α,(180°﹣α)﹣(90°﹣α)=90°,正确,不符合题意;
D、两个直角也是互补的角,故本小题错误,符合题意.
故选:D.
7.【解答】解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠1=∠AOC,
∠2=∠BOD,
∠AOE=∠COD,
∠BOE=∠COD,
∴图中相等的角有5对.
故选:A.
8.【解答】解:∵OP是∠AOB的平分线,
∴∠AOB=2∠AOP=2∠BOP,
∠AOP=∠BOP=∠AOB,
∴选项A、B、C均正确,选项D错误.
故选:D.
9.【解答】解:看内圈的数字可得:∠AOB=120°,
故选:C.
10.【解答】解:如图:
因为AM⊥BM,
所以∠2+∠3=90°,
因为南北方向的直线平行,
所以∠2=46°,∠1=∠3,
所以∠3=90°﹣∠2=90°﹣46°=44°,
所以∠1=44°,
所以起火点M在观测台A的南偏西44°,
故选:B.
二.填空题
11.【解答】解:因为两个角的度数之比为3:2,
所以设这两个角的度数分别为(3x)°和(2x)°.
根据题意,列方程,得3x+2x=180,
解这个方程,得x=36,
所以3x=108.
即较大角度数为108°.
故答案为108°.
12.【解答】解:∠α的余角=90°﹣20°20′=69°40′.
故答案为:69°40′.
13.【解答】解:如图所示,
∵AD∥BE,∠1=60°,
∴∠ABE=∠DAB=60°,
又∵∠CBE=35°,
∴∠ABC=60°﹣35°=25°.
故答案为:25.
14.【解答】解:如图,
∵CE,DB是正北方向,
∴BD∥CE,
∵∠DBA=45°,
∴∠BFC=∠DBA=45°,
∵∠ACE=15°,
∴∠BAC=∠BFC﹣∠ACE=45°﹣15°=30°.
故答案为:30.
15.【解答】解:如图:
∵点C在点A的北偏东19°,在点B的北偏西71°,
∴∠ACD=19°,∠BCD=71°,
∴∠ACB=19°+71°=90°,
∴AC2+CB2=AB2,
∵CB=9,AC=12,
∴122+92=AB2,
∴AB=15,
故答案为:15.
三.解答题
16.【解答】解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.
∵∠AOB=128°,OC平分∠AOB,
∴∠AOC=∠AOB=64°,
∵∠COD和∠AOC互余,
∴∠COD=90°﹣∠AOC=26°.
17.【解答】解:如图,由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∴∠BAC=∠BAD+∠CAD=40°+15°=55°,
∴∠CBA=∠EBC﹣∠EBA=80°﹣40°=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC
=180°﹣55°﹣40°=85°,
答:从C岛看A,B两岛的视角∠ACB的度数为85°.
18.【解答】解:(1)因为点C为OP的中点,
所以OC=2km,
因为OA=2km,
所以可得出距小明家距离相同的是学校和公园;
(2)由图可知,学校在小明家东偏北45°方向2km处,商场在小明家西偏北60°方向3.5km处,停车场在东偏南30°方向4km处.
19.【解答】解:如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠COE的度数.
小方同学的解答过程是这样的:
解:设∠COE=α,
由于已知∠BOE=2∠COE,
所以∠BOE=2α,
所以∠BOC=∠BOE+∠COE=2α+α=3α,
因为OC平分∠BOF,根据角平分线的定义,
所以∠BOC=∠FOC=3α,
因为∠EOF是直角,
所以∠EOF=90°,
所以∠EOF=∠FOC+∠COE=3α+α=4α=90°,
所以α=22.5°,
即∠COE=22.5°.
所以这一处错误是:α=22°50′.
应该修改为(从错误处开始):所以α=22.5°
