2.5 第2课时 利用二次函数求方程的近似根 课件(共34张PPT)
文档属性
| 名称 | 2.5 第2课时 利用二次函数求方程的近似根 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 07:26:21 | ||
图片预览






文档简介
(共34张PPT)
第二章 二次函数
2.5 二次函数与一元二次方程
第2课时 利用二次函数求方程的近似根
北师大版 九年级数学下册 教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
1.会用二次函数图象求一元二次方程的近似解及一元二次不等式的解集; (重点)
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.(难点)
情景导学
2
情景导学
问题:上节课我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0)之间的关系,那么如何利用二次函数图象直接求出一元二次方程的根呢
回顾与思考
新课进行时
3
新课进行时
核心知识点一
利用图象法求一元二次方程的近似根
例1:求一元二次方程 的近似根(精确到0.1).
分析:一元二次方程 x -2x-1=0 的根就是抛物线 y=x -2x-1 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.
新课进行时
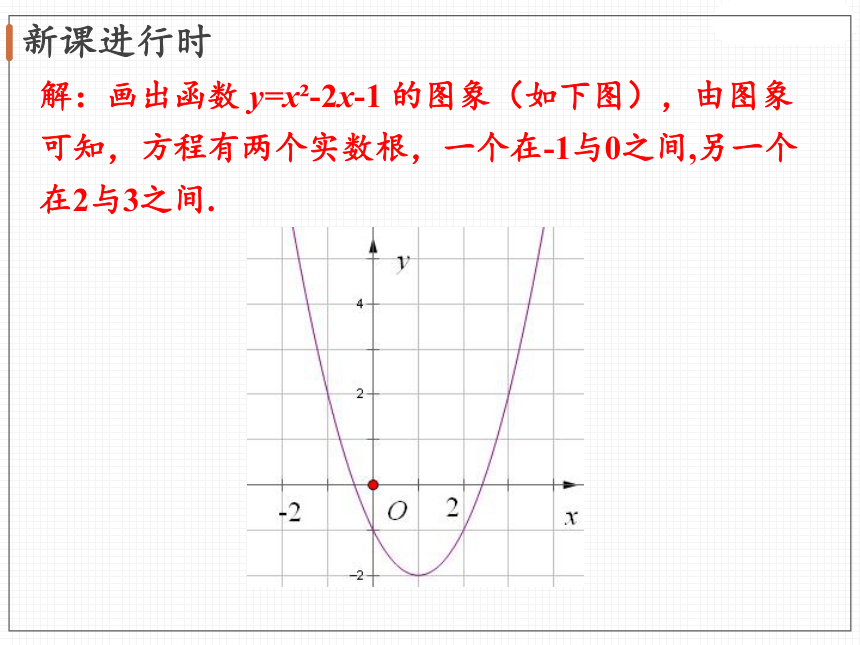
解:画出函数 y=x -2x-1 的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
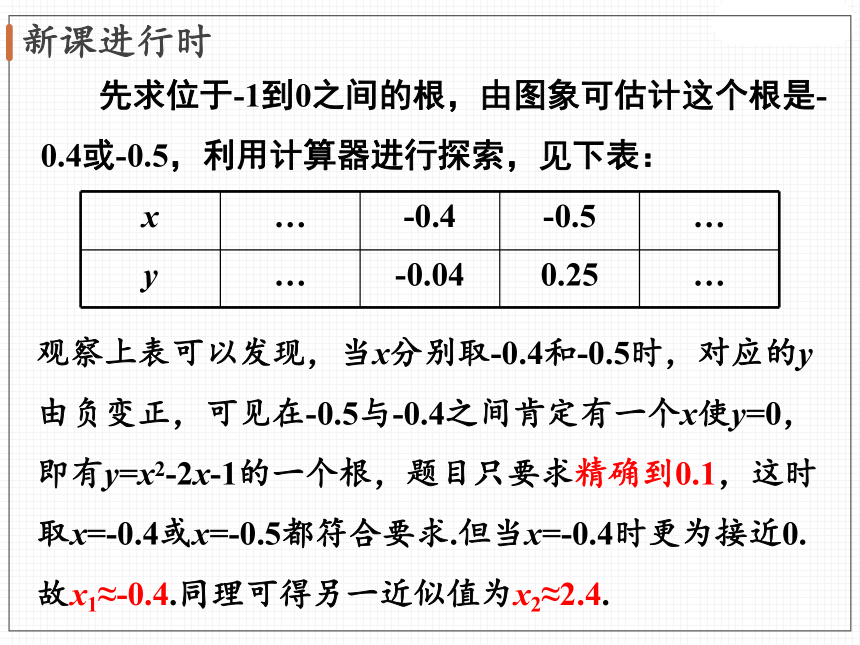
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x … -0.4 -0.5 …
y … -0.04 0.25 …
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
新课进行时
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值);
(3)确定方程ax2+bx+c=0的近似根;
方法归纳
利用图象法求一元二次方程的近似根
新课进行时
1.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A.x1≈-2.1,x2≈0.1
B.x1≈-2.5,x2≈0.5
C.x1≈-2.9,x2≈0.9
D.x1≈-3,x2≈1
解析:由图象可得二次函数y=ax2+bx+c图象的对称轴为x=-1,而对称轴右侧图象与x轴交点到原点的距离约为0.5,∴x2≈0.5;又∵对称轴为x=-1,则
=-1,∴x1=2×(-1)-0.5=-2.5.故x1≈-2.5,x2≈0.5.故选B.
B
针对训练
新课进行时
解答本题首先需要根据图象估计出一个根,再根据对称性计算出另一个根,估计值的精确程度,直接关系到计算的准确性,故估计尽量要准确.
方法总结
新课进行时
例2:求一元二次方程 的近似根(精确到0.1).
分析:令y=x -2x-1-3=x -2x-4,则x -2x-1=3的根就是抛物线 y=x -2x-4 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标.
新课进行时
2
x
y
O
解:y=x -2x-4的图象如图所示.
解:由图象可知方程的一根在3到
4之间,另一根在-1到-2之间.
(1)先求3到4之间的根.利用计算器进行探索:
x … 3.2 3.3 …
y … -0.16 0.29 …
因此,x=3.2是方程的一个近似根.
(2)可类似地求出另一个根为x=-1.2.
新课进行时
例2变式:你还能利用y=x -2x-1 的图象求一元二次方程
的近似根吗(精确到0.1)?
分析:在y=x -2x-1的图象中作直线y=3,再用图象法求出直线与抛物线交点的横坐标,则横坐标的近似值即为所求方程的近似根.
y=3
新课进行时
一元二次方程ax2+bx+c=m的根就是二次函数y=ax2+bx+c 与直线y=m(m是实数)图象交点的横坐标 .
既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.
新课进行时
方法归纳
问题1 函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=0的根是 _____ _____;
不等式ax2+bx+c>0的解集 是___________;
不等式ax2+bx+c<0的解集 是_________.
3
-1
O
x
y
x1=-1, x2=3
x<-1或x>3
-1合作探究
新课进行时
核心知识点二
利用函数的图象求一元二次不等式的解集
拓广探索:
函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是 ______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3
-1
O
x
2
(4,2)
(-2,2)
x1=-2, x2=4
x<-2或x>4
-2y
新课进行时
问题2
如果不等式ax2+bx+c>0(a≠0)的解集是x≠2 的一切实数,那么函数y=ax2+bx+c的图象与 x轴有____ 个交点,坐标是______.方程ax2+bx+c=0的根是______.
1
(2,0)
x=2
新课进行时
问题3
如果方程ax2+bx+c=0 (a≠0)没有实数根,那么函数y=ax2+bx+c的图象与 x轴有______个交点;不等式ax2+bx+c<0的解集是多少?
0
解:(1)当a>0时, ax2+bx+c<0无解;
(2)当a<0时, ax2+bx+c<0的解集是一切实数.
新课进行时
试一试:利用函数图象解下列方程和不等式:
(1) ①-x2+x+2=0;
②-x2+x+2>0;
③-x2+x+2<0.
(2) ①x2-4x+4=0;
②x2-4x+4>0;
③x2-4x+4<0.
(3) ①-x2+x-2=0;
②-x2+x-2>0;
③-x2+x-2<0.
x
y
0
2
0
x
y
-1
2
x
y
0
y= -x2+x+2
x1=-1 , x2=2
-1 < x<2
x1<-1 , x2>2
y=x2-4x+4
x=2
x≠2的一切实数
x无解
y=-x2+x-2
x无解
x无解
x为全体实数
新课进行时
要点归纳
二次函数y=ax2+bx+c的图象与x轴交点 a>0 a<0
有两个交点x1,x2 (x1<x2)
有一个交点x0
没有交点
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次不等式的关系
y<0,x1<x<x2.
y>0,x2<x或x<x1
y>0,x1<x<x2.
y<0,x2<x或x<x1
y>0,x0之外的所有实数;y<0,无解
y<0,x0之外的所有实数;y>0,无解
y>0,所有实数;y<0,无解
y<0,所有实数;y>0,无解
新课进行时
知识小结
4
知识小结
二次函数图象
由图象与x轴的交点位置,
判断方程根的近似值
一元二次方程的根
一元二次不等式的解集
随堂演练
5
随堂演练
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是( )
A. 3< x < 3.23 B. 3.23 < x < 3.24
C. 3.24x 3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
1.根据下列表格的对应值:
2.小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=-3.4,则方程的另一个近似根(精确到0.1)为( )
A.4.4 B.3.4 C.2.4 D.1.4
D
随堂演练
3.用图象法求一元二次方程 的近似根(精确到0.1).
解:画出x2+x-1=0的图象,如图所示,由图象知,方程有两个根,一个在-2和-1之间,另一个在0到1之间.通过计算器估算,可得到抛物线与x轴交点的横坐标大约为-1.6和0.6.即一元二次方程的实数根为x1≈-1.6,x2≈0.6.
随堂演练
4.已知二次函数 的图象,利用图象回答问题:
(1)方程 的解是什么?
(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?
x
y
O
2
4
8
解:(1)x1=2,x2=4;
(2)x<2或x>4;
(3)2随堂演练
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK YOU FOR LISTENING
谢谢大家!
第二章 二次函数
2.5 二次函数与一元二次方程
第2课时 利用二次函数求方程的近似根
北师大版 九年级数学下册 教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
1.会用二次函数图象求一元二次方程的近似解及一元二次不等式的解集; (重点)
2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.(难点)
情景导学
2
情景导学
问题:上节课我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0)之间的关系,那么如何利用二次函数图象直接求出一元二次方程的根呢
回顾与思考
新课进行时
3
新课进行时
核心知识点一
利用图象法求一元二次方程的近似根
例1:求一元二次方程 的近似根(精确到0.1).
分析:一元二次方程 x -2x-1=0 的根就是抛物线 y=x -2x-1 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.
新课进行时
解:画出函数 y=x -2x-1 的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x … -0.4 -0.5 …
y … -0.04 0.25 …
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
新课进行时
(1)用描点法作二次函数 y=ax2+bx+c的图象;
(2)观察估计二次函数 的图象与x轴的交点的横坐标;
(可将单位长度十等分,借助计算器确定其近似值);
(3)确定方程ax2+bx+c=0的近似根;
方法归纳
利用图象法求一元二次方程的近似根
新课进行时
1.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A.x1≈-2.1,x2≈0.1
B.x1≈-2.5,x2≈0.5
C.x1≈-2.9,x2≈0.9
D.x1≈-3,x2≈1
解析:由图象可得二次函数y=ax2+bx+c图象的对称轴为x=-1,而对称轴右侧图象与x轴交点到原点的距离约为0.5,∴x2≈0.5;又∵对称轴为x=-1,则
=-1,∴x1=2×(-1)-0.5=-2.5.故x1≈-2.5,x2≈0.5.故选B.
B
针对训练
新课进行时
解答本题首先需要根据图象估计出一个根,再根据对称性计算出另一个根,估计值的精确程度,直接关系到计算的准确性,故估计尽量要准确.
方法总结
新课进行时
例2:求一元二次方程 的近似根(精确到0.1).
分析:令y=x -2x-1-3=x -2x-4,则x -2x-1=3的根就是抛物线 y=x -2x-4 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标.
新课进行时
2
x
y
O
解:y=x -2x-4的图象如图所示.
解:由图象可知方程的一根在3到
4之间,另一根在-1到-2之间.
(1)先求3到4之间的根.利用计算器进行探索:
x … 3.2 3.3 …
y … -0.16 0.29 …
因此,x=3.2是方程的一个近似根.
(2)可类似地求出另一个根为x=-1.2.
新课进行时
例2变式:你还能利用y=x -2x-1 的图象求一元二次方程
的近似根吗(精确到0.1)?
分析:在y=x -2x-1的图象中作直线y=3,再用图象法求出直线与抛物线交点的横坐标,则横坐标的近似值即为所求方程的近似根.
y=3
新课进行时
一元二次方程ax2+bx+c=m的根就是二次函数y=ax2+bx+c 与直线y=m(m是实数)图象交点的横坐标 .
既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.
新课进行时
方法归纳
问题1 函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=0的根是 _____ _____;
不等式ax2+bx+c>0的解集 是___________;
不等式ax2+bx+c<0的解集 是_________.
3
-1
O
x
y
x1=-1, x2=3
x<-1或x>3
-1
新课进行时
核心知识点二
利用函数的图象求一元二次不等式的解集
拓广探索:
函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是 ______________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3
-1
O
x
2
(4,2)
(-2,2)
x1=-2, x2=4
x<-2或x>4
-2
新课进行时
问题2
如果不等式ax2+bx+c>0(a≠0)的解集是x≠2 的一切实数,那么函数y=ax2+bx+c的图象与 x轴有____ 个交点,坐标是______.方程ax2+bx+c=0的根是______.
1
(2,0)
x=2
新课进行时
问题3
如果方程ax2+bx+c=0 (a≠0)没有实数根,那么函数y=ax2+bx+c的图象与 x轴有______个交点;不等式ax2+bx+c<0的解集是多少?
0
解:(1)当a>0时, ax2+bx+c<0无解;
(2)当a<0时, ax2+bx+c<0的解集是一切实数.
新课进行时
试一试:利用函数图象解下列方程和不等式:
(1) ①-x2+x+2=0;
②-x2+x+2>0;
③-x2+x+2<0.
(2) ①x2-4x+4=0;
②x2-4x+4>0;
③x2-4x+4<0.
(3) ①-x2+x-2=0;
②-x2+x-2>0;
③-x2+x-2<0.
x
y
0
2
0
x
y
-1
2
x
y
0
y= -x2+x+2
x1=-1 , x2=2
-1 < x<2
x1<-1 , x2>2
y=x2-4x+4
x=2
x≠2的一切实数
x无解
y=-x2+x-2
x无解
x无解
x为全体实数
新课进行时
要点归纳
二次函数y=ax2+bx+c的图象与x轴交点 a>0 a<0
有两个交点x1,x2 (x1<x2)
有一个交点x0
没有交点
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次不等式的关系
y<0,x1<x<x2.
y>0,x2<x或x<x1
y>0,x1<x<x2.
y<0,x2<x或x<x1
y>0,x0之外的所有实数;y<0,无解
y<0,x0之外的所有实数;y>0,无解
y>0,所有实数;y<0,无解
y<0,所有实数;y>0,无解
新课进行时
知识小结
4
知识小结
二次函数图象
由图象与x轴的交点位置,
判断方程根的近似值
一元二次方程的根
一元二次不等式的解集
随堂演练
5
随堂演练
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是( )
A. 3< x < 3.23 B. 3.23 < x < 3.24
C. 3.24
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
1.根据下列表格的对应值:
2.小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=-3.4,则方程的另一个近似根(精确到0.1)为( )
A.4.4 B.3.4 C.2.4 D.1.4
D
随堂演练
3.用图象法求一元二次方程 的近似根(精确到0.1).
解:画出x2+x-1=0的图象,如图所示,由图象知,方程有两个根,一个在-2和-1之间,另一个在0到1之间.通过计算器估算,可得到抛物线与x轴交点的横坐标大约为-1.6和0.6.即一元二次方程的实数根为x1≈-1.6,x2≈0.6.
随堂演练
4.已知二次函数 的图象,利用图象回答问题:
(1)方程 的解是什么?
(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?
x
y
O
2
4
8
解:(1)x1=2,x2=4;
(2)x<2或x>4;
(3)2
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK YOU FOR LISTENING
谢谢大家!
