2019-2020学年安徽省淮北市名校联考九年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2019-2020学年安徽省淮北市名校联考九年级上学期期中数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 06:36:02 | ||
图片预览



文档简介
2019-2020学年安徽省淮北市名校联考九年级(上)期中数学试卷
一、选择题(共10小题).
1.下列函数中,一定是二次函数的是( )
A.y=﹣x2+1 B.y=ax2+bx+c C.y=2x+3 D.y=
2.已知线段a=2cm,b=8cm,它们的比例中项c是( )
A.16cm B.4cm C.±4cm D.±16cm
3.如图,点A、B分别在双曲线y=和y=上,点C、D在x轴上,且四边形ABCD为矩形,则矩形ABCD的面积为( )
A.1 B.2 C.3 D.4
4.用一根长60cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为( )
A.y=x2﹣30x(0<x<30) B.y=﹣x2+30x(0≤x<30)
C.y=﹣x2+30x(0<x<30) D.y=﹣x2+30x(0<x≤30)
5.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax﹣bc的图象大致是( )
A. B. C. D.
6.若点A(3,4)是反比例函数图象上一点,则下列说法正确的是( )
A.图象位于二、四象限
B.当x<0时,y随x的增大而减小
C.点(2,﹣6)在函数图象上
D.当y≤4时,x≥3
7.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
8.在函数y=(a为常数)的图象上有三个点(﹣1,y1),(﹣,y2),(,y3),则函数值y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
9.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=,能其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的顶点A,B分别在x轴和y轴上,与双曲线y=恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )
A.6 B.8 C.12 D.16
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知二次函数y=4x2﹣mx+5,当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,则当x=1时,y的值为 .
12.若抛物线y=x2﹣2x﹣1与x轴交于AB两点,点A与点B之间的距离用|AB|表示,则|AB|的值为 .
13.已知,点P(a,b)为直线y=x﹣2与双曲线y=的交点,则的值等于 .
14.如图,△ABC中,D、E两点分别在AB、BC上,若AD:DB=CE:EB=2:3,则△DBE的面积:△ADC的面积= .
三、(本大题共2小题,每小题8分,满分16分)
15.已知==,且2x+3y﹣z=18,求x,y,z的值.
16.已知开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5).
(1)求a的值.
(2)当x取何值时,y有最小值?并求出这个最小值.
四、(本大题共2小题,每小题8分,满分16分)
17.已知函数y=mx2﹣6x﹣7(m是常数).
(1)当m=﹣1时,该函数的图象与直线y=2有几个公共点?说明理由;
(2)若该函数的图象与x轴只有一个公共点,求m的值.
18.如图,直线y1=x+b交x轴于点B,交y轴于点A(0,2),与反比例函数的图象交于C(1,m),D(n,﹣1).
(1)求k的值;
(2)根据图象直接写出y1<y2时,x的取值范围.
五、(本大题共2小题,每小题10分,满分20分)
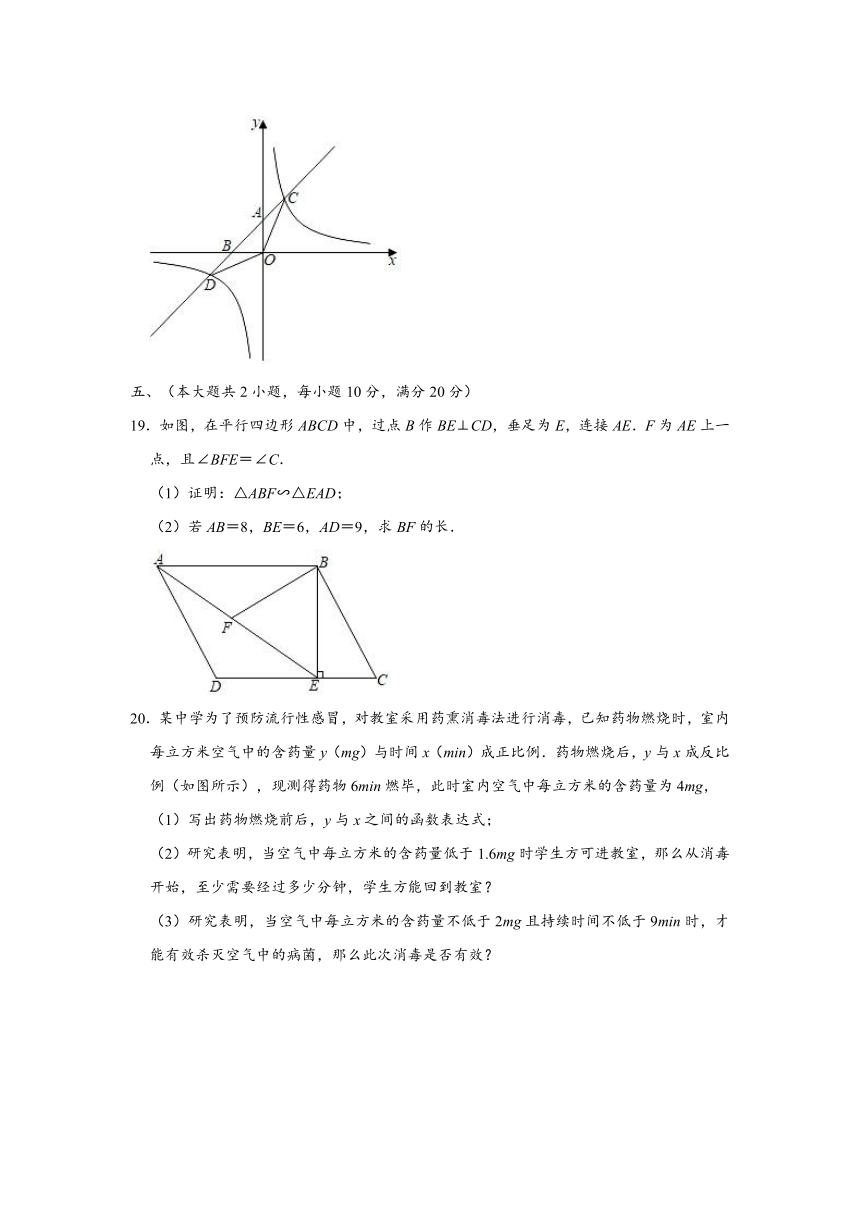
19.如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
(1)证明:△ABF∽△EAD;
(2)若AB=8,BE=6,AD=9,求BF的长.
20.某中学为了预防流行性感冒,对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
(1)写出药物燃烧前后,y与x之间的函数表达式;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生方能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于2mg且持续时间不低于9min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?
六、(本题满分12分)
21.银泰百货名创优品店购进600个钥匙扣,进价为每个8元.第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低x元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
七、(本题满分12分)
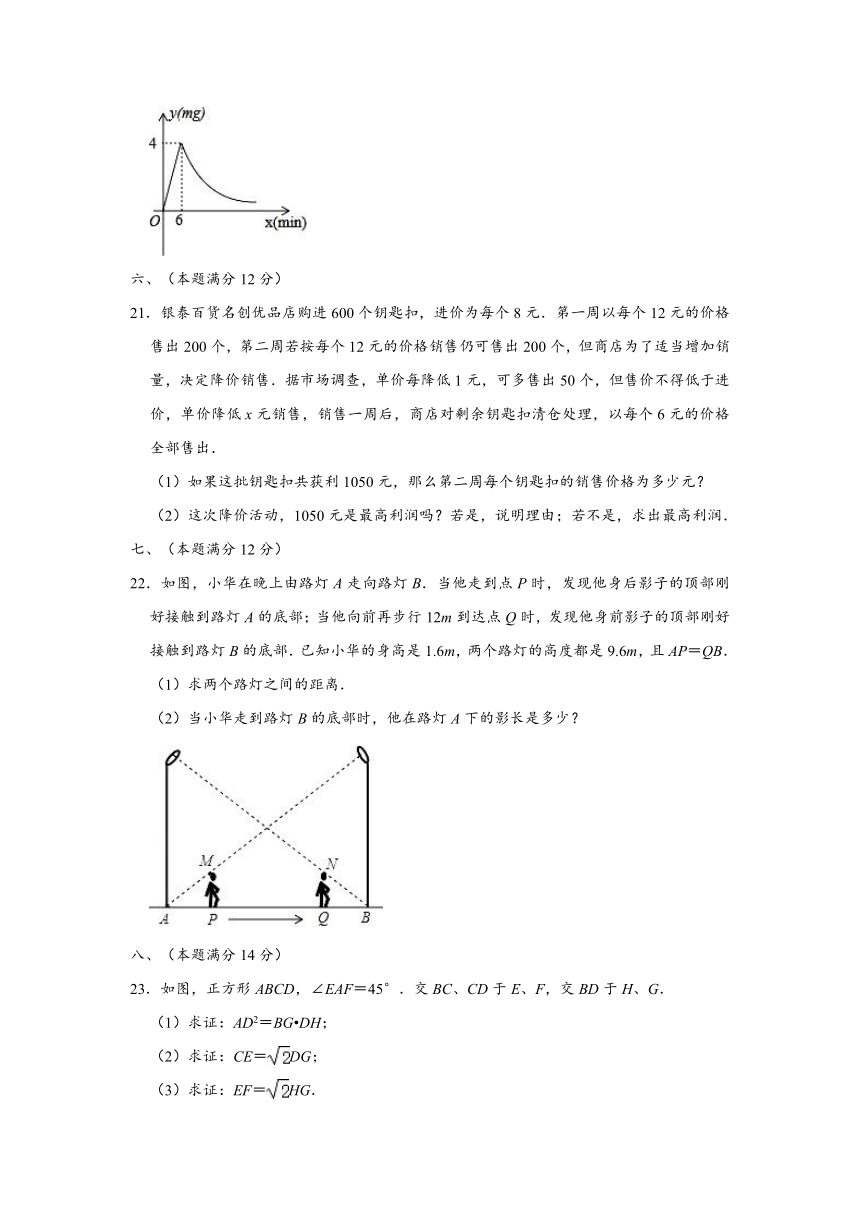
22.如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
八、(本题满分14分)
23.如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.
(1)求证:AD2=BG?DH;
(2)求证:CE=DG;
(3)求证:EF=HG.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A、B、C、D四个选项,其中只有一个是正确的。
1.下列函数中,一定是二次函数的是( )
A.y=﹣x2+1 B.y=ax2+bx+c C.y=2x+3 D.y=
【分析】根据二次函数的定义逐个判断即可.
解:A、是二次函数,故本选项符合题意;
B、当a=0时,函数不是二次函数,故本选项不符合题意;
C、不是二次函数,故本选项不符合题意;
D、不是二次函数,故本选项不符合题意;
故选:A.
2.已知线段a=2cm,b=8cm,它们的比例中项c是( )
A.16cm B.4cm C.±4cm D.±16cm
【分析】根据比例中项的定义,列出比例式即可得出中项,注意线段不能为负.
解:根据比例中项的概念结合比例的基本性质,得比例中项的平方等于两条线段的乘积.
即c2=ab,则c2=2×8,
解得c=±4,(线段是正数,负值舍去).
故选:B.
3.如图,点A、B分别在双曲线y=和y=上,点C、D在x轴上,且四边形ABCD为矩形,则矩形ABCD的面积为( )
A.1 B.2 C.3 D.4
【分析】设OD的长,根据反比例函数图象上点的坐标特征,可以表示出点A的纵坐标,即AD的长,再根据点A、B的纵坐标相等,点B在反比例函数的图象上,进而表示出OC,表示出CD,根据矩形的面积可求出面积,做出答案.
解:设OD=a,
把x=a代入y=得,y=,
即:AD=,
把y=代入y=得,x=3a,即OC=3a,
∴CD=OC﹣OD=2a,
∴矩形ABCD的面积=CD?AD=2a×=2,
故选:B.
4.用一根长60cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为( )
A.y=x2﹣30x(0<x<30) B.y=﹣x2+30x(0≤x<30)
C.y=﹣x2+30x(0<x<30) D.y=﹣x2+30x(0<x≤30)
【分析】由矩形另一边长为周长的一半减去已知边长求得另一边的长,进一步根据矩形的面积等于相邻两边长的积列出关系式即可.
解:由题意得:矩形的另一边长=60÷2﹣x=30﹣x,
矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为y=x(30﹣x)=﹣x2+30x(0<x<30).
故选:C.
5.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax﹣bc的图象大致是( )
A. B. C. D.
【分析】根据二次函数的图象可以判断a、b、c的正负,从而可以得到一次函数y=ax﹣bc的图象经过哪几个象限,本题得以解决.
解:由二次函数y=ax2+bx+c的图象可得,
a<0,b>0,c>0,
∴bc>0,
∴一次函数y=ax﹣bc的图象经过第二、三、四象限,
故选:D.
6.若点A(3,4)是反比例函数图象上一点,则下列说法正确的是( )
A.图象位于二、四象限
B.当x<0时,y随x的增大而减小
C.点(2,﹣6)在函数图象上
D.当y≤4时,x≥3
【分析】点A(3,4)是反比例函数图象上一点,可以确定|k|的值,由反比例函数的图象和性质可直接得出正确答案.,
解:∵点A(3,4)是反比例函数图象上一点,
∴|k|=3×4=12,
∴在每个象限内,y随x的增大而减少,
因此B选项是正确的,
故选:B.
7.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
【分析】利用相似三角形的判定可求解.
解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
8.在函数y=(a为常数)的图象上有三个点(﹣1,y1),(﹣,y2),(,y3),则函数值y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
【分析】先根据反比例函数的解析式判断出反比例函数的图象所在的象限及增减性,再根据各点横坐标的值判断出y1,y2,y3的大小关系即可.
解:∵反比例函数的比例系数为a2+1>0,
∴图象的两个分支在一、三象限,且在每个象限y随x的增大而减小,
∵﹣1<﹣<0,
∴点(﹣1,y1),(﹣,y2)在第三象限,
∴y2<y1<0,
∵>0,
∴点(,y3)在第一象限,
∴y3>0,
∴y2<y1<y3.
故选:A.
9.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=,能其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】根据平行线分线段成比例定理即可得到结论.
解:∵MN∥BC,
∴=,=,故①错误,③正确;
∵DN∥MC,
∴,=,故④正确;
∴=,故②正确,
故选:C.
10.如图,正方形ABCD的顶点A,B分别在x轴和y轴上,与双曲线y=恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )
A.6 B.8 C.12 D.16
【分析】过点B作x轴的平行线,过点A,C分别作y轴的平行线,两线相交于M,N,证明△ABM≌△BCN,可得BN=AM=2a,CN=BM=a,所以点C坐标为(2a,a),BC的中点E的坐标为(a,1.5a),把点E代入双曲线y=可得a的值,进而得出S△ABO的值.
解:如图,过点B作x轴的平行线,过点A,C分别作y轴的平行线,两线相交于M,N,
∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC,
∴∠ABM=90°﹣∠CBN=∠BCN,
∵∠M=∠N=90°,
∴△ABM≌△BCN(AAS),
∵OB=2OA,
∴设OA=a,OB=2a,
则BN=AM=2a,CN=BM=a,
∴点C坐标为(2a,a),
∵E为BC的中点,B(0,2a),
∴E(a,1.5a),
把点E代入双曲线y=得1.5a2=18,a2=12,
∴S△ABO=a?2a=12,
故选:C.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知二次函数y=4x2﹣mx+5,当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,则当x=1时,y的值为 25 .
【分析】因为当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,那么可知对称轴就是x=﹣2,结合顶点公式法可求出m的值,从而得出函数的解析式,再把x=1,可求出y的值.
解:∵当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,
∴对称轴x=﹣=﹣=﹣2,解得m=﹣16,
∴y=4x2+16x+5,那么当x=1时,函数y的值为25.
故答案为25.
12.若抛物线y=x2﹣2x﹣1与x轴交于AB两点,点A与点B之间的距离用|AB|表示,则|AB|的值为 2 .
【分析】通过解方程x2﹣2x﹣1=0得点A、B的坐标分别为(1+,0),(1﹣,0),然后计算点A与点B之间的距离即可.
解:当y=0时,x2﹣2x﹣1=0,解得x1=1+,x2=1﹣,
∴点A、B的坐标分别为(1+,0),(1﹣,0),
∴|AB|=1+﹣(1﹣)=2.
故答案为2.
13.已知,点P(a,b)为直线y=x﹣2与双曲线y=的交点,则的值等于 ﹣2 .
【分析】将点P分别代入两函数解析式得到:b=a﹣2,b=﹣,进而得到a﹣b=2,ab=﹣1.将其代入求值即可.
解:∵点P(a,b)为直线y=x﹣2与双曲线y=的交点,
∴b=a﹣2,b=﹣,
∴a﹣b=2,ab=﹣1.
∴===﹣2.
故答案是:﹣2.
14.如图,△ABC中,D、E两点分别在AB、BC上,若AD:DB=CE:EB=2:3,则△DBE的面积:△ADC的面积= .
【分析】先证△BED与△BCA相似,求出△BED与△BCA的相似比,进一步求出其面积比,然后分别过点B,D作AC的垂线BM,DN,求出DN与BM的比值,推出△DCA与△BCA的面积比,结合△BED与△BCA的面积比即可求出最终结果.
解:∵==,
∴==,
又∵∠DBE=∠ABC,
∴△BED∽△BCA,
∴==,
分别过点B,D作AC的垂线BM,DN,
则DN∥BM,
∴△ADN∽△ABM,
∴==,
∵S△ADC=AC?DN,S△BCA=AC?BM,
∴===,
∴=×=,
故答案为:.
三、(本大题共2小题,每小题8分,满分16分)
15.已知==,且2x+3y﹣z=18,求x,y,z的值.
【分析】根据比例的性质,可用x表示y,用x表示z,根据解方程,可得答案.
解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
16.已知开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5).
(1)求a的值.
(2)当x取何值时,y有最小值?并求出这个最小值.
【分析】(1)根据开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5),可以求得a的值;
(2)根据(1)中a的值,可以将抛物线化为顶点式,从而可以解答本题.
解:(1)∵开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5),
∴,
解得,a=1,
即a的值是1;
(2)由(1)知a=1,
则y=x2﹣4x+1﹣6=x2﹣4x﹣5=(x﹣2)2﹣9,
∴当x=2时,y取得最小值,这个最小值是﹣9.
四、(本大题共2小题,每小题8分,满分16分)
17.已知函数y=mx2﹣6x﹣7(m是常数).
(1)当m=﹣1时,该函数的图象与直线y=2有几个公共点?说明理由;
(2)若该函数的图象与x轴只有一个公共点,求m的值.
【分析】(1)转化为求方程组的解,即可判断;
(2)分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用判别式△=0,转化为方程即可解决问题;
解:(1)m=﹣1时,,解得,
∴该函数的图象与直线y=2有1个公共点.
(2)①当m=0时,函数y=﹣4x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2﹣6x﹣7的图象与x轴只有一个交点,则方程mx2﹣6x﹣7=0有两个相等的实数根,
所以△=(﹣6)2﹣4m?(﹣7)=0,m=﹣.
综上,若函数y=mx2﹣4x+1的图象与x轴只有一个交点,则m的值为0或﹣.
18.如图,直线y1=x+b交x轴于点B,交y轴于点A(0,2),与反比例函数的图象交于C(1,m),D(n,﹣1).
(1)求k的值;
(2)根据图象直接写出y1<y2时,x的取值范围.
【分析】(1)把A的坐标代入y1=x+b求出b,即可得出一次函数的表达式,把C(1,m),D(n,﹣1)代入求出C、D的坐标,把C的坐标代入y2=的,求出k即可;
(2)根据C、D的坐标和图象得出即可.
解:(1)把A(0,2)代入y1=x+b得:b=2,
即一次函数的表达式为y1=x+2,
把C(1,m),D(n,﹣1)代入得:m=1+2,﹣1=n+2,
解得m=3,n=﹣3,
即C(1,3),D(﹣3,﹣1),
把C的坐标代入y2=得:3=,
解得:k=3;
(2)由图象可知:y1<y2时,x的取值范围是x<﹣3或0<x<1.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
(1)证明:△ABF∽△EAD;
(2)若AB=8,BE=6,AD=9,求BF的长.
【分析】(1)可通过证明∠BAF=∠AED,∠AFB=∠D,证得△ABF∽△EAD;
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.可在直角三角形ABE中用勾股定理求出AE的长,即可求解.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠D+∠C=180°,∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB,
∴∠ABE=90°,AB=8,BE=6,
∴AE=10,
∵由(1)知,△ABF∽△EAD,
∴=,即=,
∴BF=.
20.某中学为了预防流行性感冒,对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
(1)写出药物燃烧前后,y与x之间的函数表达式;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生方能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于2mg且持续时间不低于9min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?
【分析】(1)药物燃烧时,设出y与x之间的解析式y=k1x,把点(6,4)代入即可,药物燃烧后,设出y与x之间的解析式(k2>0)代入(6,4)即可;
(2)把y=1.6代入反比例函数解析式,求出相应的x;
(3)把y=2代入正比例函数解析式和反比例函数解析式,求出相应的x,两数之差与9进行比较,≥9就有效.
解:(1)设药物燃烧时y关于x的函数关系式为:y=k1x(k1>0)代入(6,4)为4=6k1
∴k1=,
设药物燃烧后y关于x的函数关系式为:(k2>0)代入(6,4)为:4=,
∴k2=24,
∴药物燃烧时y关于x的函数关系式为:y=x(0≤x≤6),药物燃烧后y关于x的函数关系式为:y=(x>6);
(2)令y=中y<1.6,得:x>15,
即从消毒开始,至少需要15分钟后学生才能进入教室;
(3)把y=2代入y=x,得:x=3,
把y=2代入y=,得:x=12,
∵12﹣3=9,
所以这次消毒是有效的.
六、(本题满分12分)
21.银泰百货名创优品店购进600个钥匙扣,进价为每个8元.第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低x元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
【分析】(1)设获利为w,根据每周的利润等于每周的销售量乘以(售价﹣进价),再将它们加起来,即可得w关于x的函数,然后让其等于1050,解方程即可;
(2)将(1)中的利润函数写成顶点式,即可知最大值,从而可得结论.
解:(1)∵第二周每个旅游纪念品的销售价格为(12﹣x)元,设获利为w,由题意得:
w=200×(12﹣8)+(12﹣x﹣8)(200+50x)+(6﹣8)[(600﹣200)﹣(200+50x)]
=800+50(4﹣x)(4+x)﹣2(200﹣50x)
=800+800﹣50x2﹣400+100x
=﹣50x2+100x+1200
如果这批钥匙扣共获利1050元,则﹣50x2+100x+1200=1050
∴x2﹣2x﹣3=0
∴(x﹣3)(x+1)=0
∴x=3或x=﹣1(舍)
∴12﹣3=9(元)
∴第二周每个钥匙扣的销售价格为9元.
(2)∵w=﹣50x2+100x+1200
=﹣50(x﹣1)2+1250
∴当x=1时,w有最大值,最大值为1250元.
∴这次降价活动,1050元不是最高利润,最高利润是1250元.
七、(本题满分12分)
22.如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
【分析】(1)如图1,先证明△APM∽△ABD,利用相似比可得AP=AB,再证明△BQN∽△BAC,利用相似比可得BQ=AB,则AB+12+AB=AB,解得AB=18(m);
(2)如图2,他在路灯A下的影子为BN,证明△NBM∽△NAC,利用相似三角形的性质得=,然后利用比例性质求出BN即可.
解:(1)如图1,
∵PM∥BD,
∴△APM∽△ABD,
=,即=,
∴AP=AB,
∵NQ∥AC,
∴△BNQ∽△BCA,
∴=,即=,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴=,即=,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
八、(本题满分14分)
23.如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.
(1)求证:AD2=BG?DH;
(2)求证:CE=DG;
(3)求证:EF=HG.
【分析】(1)易证∠BAG=∠AHD,∠ABD=∠ADB=45°,即可证明△ABG∽△HDA,可得,即可得出结论;
(2)首先连接AC,由正方形ABCD,∠EAF=45゜,易证得∠ACE=∠ADN=∠CAD=45°,AC=AD,继而可得∠EAC=∠NAD,则可证得△EAC∽△NAD,然后由相似三角形的对应边成比例,证得结论;
(3)根据两边的比相等,且夹角相等证明△GAH∽△EAF,得,所以EF=GH.
【解答】证明:(1)∵四边形ABCD为正方形
∴∠ABD=∠ADB=45°,AB=AD,
∵∠EAF=45°
∴∠BAG=45°+∠BAH,∠AHD=45°+∠BAH,
∴∠BAG=∠AHD,
又∵∠ABD=∠ADB=45°,
∴△ABG∽△HDA,
∴,
∴BG?DH=AB?AD=AD2;
(2)如图,连接AC,
∵四边形ABCD是正方形
∴∠ACE=∠ADB=∠CAD=45°,
∴AC=AD,
∵∠EAF=45°,
∴∠EAF=∠CAD,
∴∠EAF﹣∠CAF=∠CAD﹣∠CAF,
∴∠EAC=∠GAD,
∴△EAC∽△GAD,
∴,
∴CE=DG;
(3)由(2)得:△EAC∽△GAD,
∴,
同理得:△AFC∽△AHB,
∴,
∴,
∴,
∵∠GAH=∠EAF,
∴△GAH∽△EAF,
∴,
∴EF=GH.
一、选择题(共10小题).
1.下列函数中,一定是二次函数的是( )
A.y=﹣x2+1 B.y=ax2+bx+c C.y=2x+3 D.y=
2.已知线段a=2cm,b=8cm,它们的比例中项c是( )
A.16cm B.4cm C.±4cm D.±16cm
3.如图,点A、B分别在双曲线y=和y=上,点C、D在x轴上,且四边形ABCD为矩形,则矩形ABCD的面积为( )
A.1 B.2 C.3 D.4
4.用一根长60cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为( )
A.y=x2﹣30x(0<x<30) B.y=﹣x2+30x(0≤x<30)
C.y=﹣x2+30x(0<x<30) D.y=﹣x2+30x(0<x≤30)
5.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax﹣bc的图象大致是( )
A. B. C. D.
6.若点A(3,4)是反比例函数图象上一点,则下列说法正确的是( )
A.图象位于二、四象限
B.当x<0时,y随x的增大而减小
C.点(2,﹣6)在函数图象上
D.当y≤4时,x≥3
7.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
8.在函数y=(a为常数)的图象上有三个点(﹣1,y1),(﹣,y2),(,y3),则函数值y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
9.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=,能其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
10.如图,正方形ABCD的顶点A,B分别在x轴和y轴上,与双曲线y=恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )
A.6 B.8 C.12 D.16
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知二次函数y=4x2﹣mx+5,当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,则当x=1时,y的值为 .
12.若抛物线y=x2﹣2x﹣1与x轴交于AB两点,点A与点B之间的距离用|AB|表示,则|AB|的值为 .
13.已知,点P(a,b)为直线y=x﹣2与双曲线y=的交点,则的值等于 .
14.如图,△ABC中,D、E两点分别在AB、BC上,若AD:DB=CE:EB=2:3,则△DBE的面积:△ADC的面积= .
三、(本大题共2小题,每小题8分,满分16分)
15.已知==,且2x+3y﹣z=18,求x,y,z的值.
16.已知开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5).
(1)求a的值.
(2)当x取何值时,y有最小值?并求出这个最小值.
四、(本大题共2小题,每小题8分,满分16分)
17.已知函数y=mx2﹣6x﹣7(m是常数).
(1)当m=﹣1时,该函数的图象与直线y=2有几个公共点?说明理由;
(2)若该函数的图象与x轴只有一个公共点,求m的值.
18.如图,直线y1=x+b交x轴于点B,交y轴于点A(0,2),与反比例函数的图象交于C(1,m),D(n,﹣1).
(1)求k的值;
(2)根据图象直接写出y1<y2时,x的取值范围.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
(1)证明:△ABF∽△EAD;
(2)若AB=8,BE=6,AD=9,求BF的长.
20.某中学为了预防流行性感冒,对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
(1)写出药物燃烧前后,y与x之间的函数表达式;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生方能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于2mg且持续时间不低于9min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?
六、(本题满分12分)
21.银泰百货名创优品店购进600个钥匙扣,进价为每个8元.第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低x元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
七、(本题满分12分)
22.如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
八、(本题满分14分)
23.如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.
(1)求证:AD2=BG?DH;
(2)求证:CE=DG;
(3)求证:EF=HG.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A、B、C、D四个选项,其中只有一个是正确的。
1.下列函数中,一定是二次函数的是( )
A.y=﹣x2+1 B.y=ax2+bx+c C.y=2x+3 D.y=
【分析】根据二次函数的定义逐个判断即可.
解:A、是二次函数,故本选项符合题意;
B、当a=0时,函数不是二次函数,故本选项不符合题意;
C、不是二次函数,故本选项不符合题意;
D、不是二次函数,故本选项不符合题意;
故选:A.
2.已知线段a=2cm,b=8cm,它们的比例中项c是( )
A.16cm B.4cm C.±4cm D.±16cm
【分析】根据比例中项的定义,列出比例式即可得出中项,注意线段不能为负.
解:根据比例中项的概念结合比例的基本性质,得比例中项的平方等于两条线段的乘积.
即c2=ab,则c2=2×8,
解得c=±4,(线段是正数,负值舍去).
故选:B.
3.如图,点A、B分别在双曲线y=和y=上,点C、D在x轴上,且四边形ABCD为矩形,则矩形ABCD的面积为( )
A.1 B.2 C.3 D.4
【分析】设OD的长,根据反比例函数图象上点的坐标特征,可以表示出点A的纵坐标,即AD的长,再根据点A、B的纵坐标相等,点B在反比例函数的图象上,进而表示出OC,表示出CD,根据矩形的面积可求出面积,做出答案.
解:设OD=a,
把x=a代入y=得,y=,
即:AD=,
把y=代入y=得,x=3a,即OC=3a,
∴CD=OC﹣OD=2a,
∴矩形ABCD的面积=CD?AD=2a×=2,
故选:B.
4.用一根长60cm的铁丝围成一个矩形,那么矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为( )
A.y=x2﹣30x(0<x<30) B.y=﹣x2+30x(0≤x<30)
C.y=﹣x2+30x(0<x<30) D.y=﹣x2+30x(0<x≤30)
【分析】由矩形另一边长为周长的一半减去已知边长求得另一边的长,进一步根据矩形的面积等于相邻两边长的积列出关系式即可.
解:由题意得:矩形的另一边长=60÷2﹣x=30﹣x,
矩形的面积y(cm2)与它的一边长x(cm)之间的函数关系式为y=x(30﹣x)=﹣x2+30x(0<x<30).
故选:C.
5.二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax﹣bc的图象大致是( )
A. B. C. D.
【分析】根据二次函数的图象可以判断a、b、c的正负,从而可以得到一次函数y=ax﹣bc的图象经过哪几个象限,本题得以解决.
解:由二次函数y=ax2+bx+c的图象可得,
a<0,b>0,c>0,
∴bc>0,
∴一次函数y=ax﹣bc的图象经过第二、三、四象限,
故选:D.
6.若点A(3,4)是反比例函数图象上一点,则下列说法正确的是( )
A.图象位于二、四象限
B.当x<0时,y随x的增大而减小
C.点(2,﹣6)在函数图象上
D.当y≤4时,x≥3
【分析】点A(3,4)是反比例函数图象上一点,可以确定|k|的值,由反比例函数的图象和性质可直接得出正确答案.,
解:∵点A(3,4)是反比例函数图象上一点,
∴|k|=3×4=12,
∴在每个象限内,y随x的增大而减少,
因此B选项是正确的,
故选:B.
7.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B B.∠APC=∠ACB
C.AP:AC=AC:AB D.AP:AB=PC:BC
【分析】利用相似三角形的判定可求解.
解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
8.在函数y=(a为常数)的图象上有三个点(﹣1,y1),(﹣,y2),(,y3),则函数值y1、y2、y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
【分析】先根据反比例函数的解析式判断出反比例函数的图象所在的象限及增减性,再根据各点横坐标的值判断出y1,y2,y3的大小关系即可.
解:∵反比例函数的比例系数为a2+1>0,
∴图象的两个分支在一、三象限,且在每个象限y随x的增大而减小,
∵﹣1<﹣<0,
∴点(﹣1,y1),(﹣,y2)在第三象限,
∴y2<y1<0,
∵>0,
∴点(,y3)在第一象限,
∴y3>0,
∴y2<y1<y3.
故选:A.
9.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=,能其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】根据平行线分线段成比例定理即可得到结论.
解:∵MN∥BC,
∴=,=,故①错误,③正确;
∵DN∥MC,
∴,=,故④正确;
∴=,故②正确,
故选:C.
10.如图,正方形ABCD的顶点A,B分别在x轴和y轴上,与双曲线y=恰好交于BC的中点E,若OB=2OA,则S△ABO的值为( )
A.6 B.8 C.12 D.16
【分析】过点B作x轴的平行线,过点A,C分别作y轴的平行线,两线相交于M,N,证明△ABM≌△BCN,可得BN=AM=2a,CN=BM=a,所以点C坐标为(2a,a),BC的中点E的坐标为(a,1.5a),把点E代入双曲线y=可得a的值,进而得出S△ABO的值.
解:如图,过点B作x轴的平行线,过点A,C分别作y轴的平行线,两线相交于M,N,
∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC,
∴∠ABM=90°﹣∠CBN=∠BCN,
∵∠M=∠N=90°,
∴△ABM≌△BCN(AAS),
∵OB=2OA,
∴设OA=a,OB=2a,
则BN=AM=2a,CN=BM=a,
∴点C坐标为(2a,a),
∵E为BC的中点,B(0,2a),
∴E(a,1.5a),
把点E代入双曲线y=得1.5a2=18,a2=12,
∴S△ABO=a?2a=12,
故选:C.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知二次函数y=4x2﹣mx+5,当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,则当x=1时,y的值为 25 .
【分析】因为当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,那么可知对称轴就是x=﹣2,结合顶点公式法可求出m的值,从而得出函数的解析式,再把x=1,可求出y的值.
解:∵当x≤﹣2时,y随x的增大而减小;当x≥﹣2时,y随x的增大而增大,
∴对称轴x=﹣=﹣=﹣2,解得m=﹣16,
∴y=4x2+16x+5,那么当x=1时,函数y的值为25.
故答案为25.
12.若抛物线y=x2﹣2x﹣1与x轴交于AB两点,点A与点B之间的距离用|AB|表示,则|AB|的值为 2 .
【分析】通过解方程x2﹣2x﹣1=0得点A、B的坐标分别为(1+,0),(1﹣,0),然后计算点A与点B之间的距离即可.
解:当y=0时,x2﹣2x﹣1=0,解得x1=1+,x2=1﹣,
∴点A、B的坐标分别为(1+,0),(1﹣,0),
∴|AB|=1+﹣(1﹣)=2.
故答案为2.
13.已知,点P(a,b)为直线y=x﹣2与双曲线y=的交点,则的值等于 ﹣2 .
【分析】将点P分别代入两函数解析式得到:b=a﹣2,b=﹣,进而得到a﹣b=2,ab=﹣1.将其代入求值即可.
解:∵点P(a,b)为直线y=x﹣2与双曲线y=的交点,
∴b=a﹣2,b=﹣,
∴a﹣b=2,ab=﹣1.
∴===﹣2.
故答案是:﹣2.
14.如图,△ABC中,D、E两点分别在AB、BC上,若AD:DB=CE:EB=2:3,则△DBE的面积:△ADC的面积= .
【分析】先证△BED与△BCA相似,求出△BED与△BCA的相似比,进一步求出其面积比,然后分别过点B,D作AC的垂线BM,DN,求出DN与BM的比值,推出△DCA与△BCA的面积比,结合△BED与△BCA的面积比即可求出最终结果.
解:∵==,
∴==,
又∵∠DBE=∠ABC,
∴△BED∽△BCA,
∴==,
分别过点B,D作AC的垂线BM,DN,
则DN∥BM,
∴△ADN∽△ABM,
∴==,
∵S△ADC=AC?DN,S△BCA=AC?BM,
∴===,
∴=×=,
故答案为:.
三、(本大题共2小题,每小题8分,满分16分)
15.已知==,且2x+3y﹣z=18,求x,y,z的值.
【分析】根据比例的性质,可用x表示y,用x表示z,根据解方程,可得答案.
解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
16.已知开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5).
(1)求a的值.
(2)当x取何值时,y有最小值?并求出这个最小值.
【分析】(1)根据开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5),可以求得a的值;
(2)根据(1)中a的值,可以将抛物线化为顶点式,从而可以解答本题.
解:(1)∵开口向上的抛物线y=ax2﹣4x+|a|﹣6经过点(0,﹣5),
∴,
解得,a=1,
即a的值是1;
(2)由(1)知a=1,
则y=x2﹣4x+1﹣6=x2﹣4x﹣5=(x﹣2)2﹣9,
∴当x=2时,y取得最小值,这个最小值是﹣9.
四、(本大题共2小题,每小题8分,满分16分)
17.已知函数y=mx2﹣6x﹣7(m是常数).
(1)当m=﹣1时,该函数的图象与直线y=2有几个公共点?说明理由;
(2)若该函数的图象与x轴只有一个公共点,求m的值.
【分析】(1)转化为求方程组的解,即可判断;
(2)分两种情况讨论:①当函数为一次函数时,与x轴有一个交点;
②当函数为二次函数时,利用判别式△=0,转化为方程即可解决问题;
解:(1)m=﹣1时,,解得,
∴该函数的图象与直线y=2有1个公共点.
(2)①当m=0时,函数y=﹣4x+1的图象与x轴只有一个交点;
②当m≠0时,若函数y=mx2﹣6x﹣7的图象与x轴只有一个交点,则方程mx2﹣6x﹣7=0有两个相等的实数根,
所以△=(﹣6)2﹣4m?(﹣7)=0,m=﹣.
综上,若函数y=mx2﹣4x+1的图象与x轴只有一个交点,则m的值为0或﹣.
18.如图,直线y1=x+b交x轴于点B,交y轴于点A(0,2),与反比例函数的图象交于C(1,m),D(n,﹣1).
(1)求k的值;
(2)根据图象直接写出y1<y2时,x的取值范围.
【分析】(1)把A的坐标代入y1=x+b求出b,即可得出一次函数的表达式,把C(1,m),D(n,﹣1)代入求出C、D的坐标,把C的坐标代入y2=的,求出k即可;
(2)根据C、D的坐标和图象得出即可.
解:(1)把A(0,2)代入y1=x+b得:b=2,
即一次函数的表达式为y1=x+2,
把C(1,m),D(n,﹣1)代入得:m=1+2,﹣1=n+2,
解得m=3,n=﹣3,
即C(1,3),D(﹣3,﹣1),
把C的坐标代入y2=得:3=,
解得:k=3;
(2)由图象可知:y1<y2时,x的取值范围是x<﹣3或0<x<1.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
(1)证明:△ABF∽△EAD;
(2)若AB=8,BE=6,AD=9,求BF的长.
【分析】(1)可通过证明∠BAF=∠AED,∠AFB=∠D,证得△ABF∽△EAD;
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.可在直角三角形ABE中用勾股定理求出AE的长,即可求解.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠D+∠C=180°,∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD;
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB,
∴∠ABE=90°,AB=8,BE=6,
∴AE=10,
∵由(1)知,△ABF∽△EAD,
∴=,即=,
∴BF=.
20.某中学为了预防流行性感冒,对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物6min燃毕,此时室内空气中每立方米的含药量为4mg,
(1)写出药物燃烧前后,y与x之间的函数表达式;
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟,学生方能回到教室?
(3)研究表明,当空气中每立方米的含药量不低于2mg且持续时间不低于9min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?
【分析】(1)药物燃烧时,设出y与x之间的解析式y=k1x,把点(6,4)代入即可,药物燃烧后,设出y与x之间的解析式(k2>0)代入(6,4)即可;
(2)把y=1.6代入反比例函数解析式,求出相应的x;
(3)把y=2代入正比例函数解析式和反比例函数解析式,求出相应的x,两数之差与9进行比较,≥9就有效.
解:(1)设药物燃烧时y关于x的函数关系式为:y=k1x(k1>0)代入(6,4)为4=6k1
∴k1=,
设药物燃烧后y关于x的函数关系式为:(k2>0)代入(6,4)为:4=,
∴k2=24,
∴药物燃烧时y关于x的函数关系式为:y=x(0≤x≤6),药物燃烧后y关于x的函数关系式为:y=(x>6);
(2)令y=中y<1.6,得:x>15,
即从消毒开始,至少需要15分钟后学生才能进入教室;
(3)把y=2代入y=x,得:x=3,
把y=2代入y=,得:x=12,
∵12﹣3=9,
所以这次消毒是有效的.
六、(本题满分12分)
21.银泰百货名创优品店购进600个钥匙扣,进价为每个8元.第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低x元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
【分析】(1)设获利为w,根据每周的利润等于每周的销售量乘以(售价﹣进价),再将它们加起来,即可得w关于x的函数,然后让其等于1050,解方程即可;
(2)将(1)中的利润函数写成顶点式,即可知最大值,从而可得结论.
解:(1)∵第二周每个旅游纪念品的销售价格为(12﹣x)元,设获利为w,由题意得:
w=200×(12﹣8)+(12﹣x﹣8)(200+50x)+(6﹣8)[(600﹣200)﹣(200+50x)]
=800+50(4﹣x)(4+x)﹣2(200﹣50x)
=800+800﹣50x2﹣400+100x
=﹣50x2+100x+1200
如果这批钥匙扣共获利1050元,则﹣50x2+100x+1200=1050
∴x2﹣2x﹣3=0
∴(x﹣3)(x+1)=0
∴x=3或x=﹣1(舍)
∴12﹣3=9(元)
∴第二周每个钥匙扣的销售价格为9元.
(2)∵w=﹣50x2+100x+1200
=﹣50(x﹣1)2+1250
∴当x=1时,w有最大值,最大值为1250元.
∴这次降价活动,1050元不是最高利润,最高利润是1250元.
七、(本题满分12分)
22.如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离.
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?
【分析】(1)如图1,先证明△APM∽△ABD,利用相似比可得AP=AB,再证明△BQN∽△BAC,利用相似比可得BQ=AB,则AB+12+AB=AB,解得AB=18(m);
(2)如图2,他在路灯A下的影子为BN,证明△NBM∽△NAC,利用相似三角形的性质得=,然后利用比例性质求出BN即可.
解:(1)如图1,
∵PM∥BD,
∴△APM∽△ABD,
=,即=,
∴AP=AB,
∵NQ∥AC,
∴△BNQ∽△BCA,
∴=,即=,
∴BQ=AB,
而AP+PQ+BQ=AB,
∴AB+12+AB=AB,
∴AB=18.
答:两路灯的距离为18m;
(2)如图2,他在路灯A下的影子为BN,
∵BM∥AC,
∴△NBM∽△NAC,
∴=,即=,解得BN=3.6.
答:当他走到路灯B时,他在路灯A下的影长是3.6m.
八、(本题满分14分)
23.如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.
(1)求证:AD2=BG?DH;
(2)求证:CE=DG;
(3)求证:EF=HG.
【分析】(1)易证∠BAG=∠AHD,∠ABD=∠ADB=45°,即可证明△ABG∽△HDA,可得,即可得出结论;
(2)首先连接AC,由正方形ABCD,∠EAF=45゜,易证得∠ACE=∠ADN=∠CAD=45°,AC=AD,继而可得∠EAC=∠NAD,则可证得△EAC∽△NAD,然后由相似三角形的对应边成比例,证得结论;
(3)根据两边的比相等,且夹角相等证明△GAH∽△EAF,得,所以EF=GH.
【解答】证明:(1)∵四边形ABCD为正方形
∴∠ABD=∠ADB=45°,AB=AD,
∵∠EAF=45°
∴∠BAG=45°+∠BAH,∠AHD=45°+∠BAH,
∴∠BAG=∠AHD,
又∵∠ABD=∠ADB=45°,
∴△ABG∽△HDA,
∴,
∴BG?DH=AB?AD=AD2;
(2)如图,连接AC,
∵四边形ABCD是正方形
∴∠ACE=∠ADB=∠CAD=45°,
∴AC=AD,
∵∠EAF=45°,
∴∠EAF=∠CAD,
∴∠EAF﹣∠CAF=∠CAD﹣∠CAF,
∴∠EAC=∠GAD,
∴△EAC∽△GAD,
∴,
∴CE=DG;
(3)由(2)得:△EAC∽△GAD,
∴,
同理得:△AFC∽△AHB,
∴,
∴,
∴,
∵∠GAH=∠EAF,
∴△GAH∽△EAF,
∴,
∴EF=GH.
同课章节目录
