人教版五年级上册数学教学课件- 商的近似数(25张ppt)
文档属性
| 名称 | 人教版五年级上册数学教学课件- 商的近似数(25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 28.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 12:23:35 | ||
图片预览








文档简介
商的近似数
2.8 3
× 0.9
2.5 4 7
2.83×0.9
2.83×0.9 ≈ 2.5
4
2.83×0.9 ≈ 2.55
7
小飞
结果保留一位小数
结果保留两位小数
四舍五入
小彤
文文
什么时候需要求商的近似数?
求商的近似数和求积的近似数,方法一样吗?
小亮
资料
资料
这筒羽毛球19.86元。
一筒是12个。
小丁
每个羽毛球大约多少钱?
可以写一写、算一算,求出每个羽毛球大约多少钱?
小飞
商的近似数
小锐
芳芳
( )
1 9 . 8 6
1 2
1 2
7
7 2
6 6
1 . 6 5 5
6 0
6 0
6 0
0
8
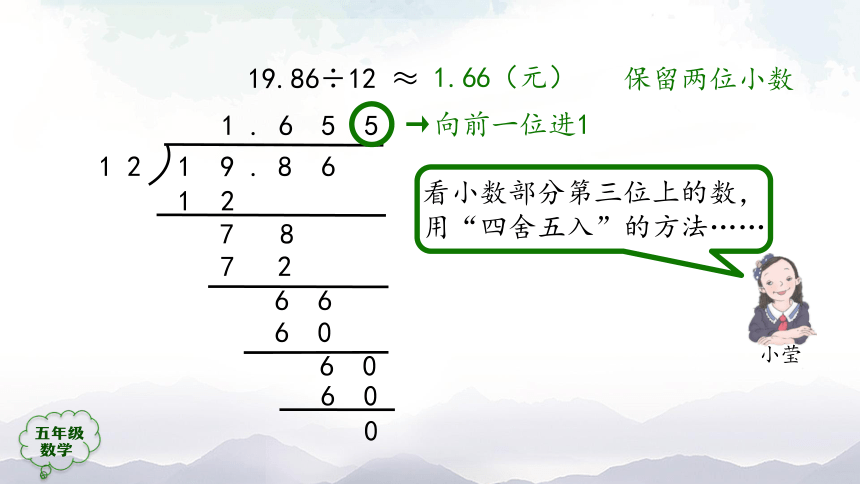
19.86÷12 ≈
→向前一位进1
看小数部分第三位上的数,用“四舍五入”的方法……
保留两位小数
1.66(元)
小莹
1 9 . 8 6
1 2
1 2
7
7 2
6 6
1 . 6 5 5
6 0
6 0
6 0
0
8
19.86÷12 ≈
小亮
保留一位小数
看小数部分第二位上的数,用“四舍五入”的方法……
1.7(元)
文文
什么时候需要求商的近似数?
在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
优惠促销
羽毛球每筒12个,售价18.5元。
小涵
平均每个羽毛球大约多少钱?
请你算一算每个羽毛球大约多少钱?(保留两位小数)
小涵
平均每个羽毛球大约多少钱?
优惠促销
羽毛球每筒12个,售价18.5元。
18.5÷12 ≈ (保留两位小数)
小丁
必须算完才能求商的近似数吗?
小锐
小彤
舍
小亮
小涵
小锐
文文
18.5÷12 ≈ (保留两位小数)
( )
1.54(元)
(保留三位小数)
1.5 4 2
1 8 .5
1 2
1 2
6 5
6 0
5 0
1 .5 4 1 6
4 8
2 0
1 2
8 0
1 8.5 ÷ 1 2 ≈
7 2
8
小刚
保留三位小数,计算到小数部分第四位……
1 8 .5
1 2
1 2
6 5
6 0
5 0
1 .5 4 1 6 6
4 8
2 0
1 2
8 0
7 2
8 0
7 2
8
(保留四位小数)
1.5 4 1 7
小涵
保留四位小数,计算到小数部分第五位……
1 8.5 ÷ 1 2 ≈
求商的近似数时,计算到比保留的小数位数多一位,再将最后一位“四舍五入”。
小丁
说一说,怎样求商的近似数?
老师
小涵
保留四位小数,计算到小数部分第五位……
小刚
保留三位小数,计算到小数部分第四位……
小勇
小莹
没计算到小数部分第三位,怎么求近似数?
添“0”继续除,最多商“1”……
小勇
芳芳
估出下一位的商是几,就可以用“四舍五入”的方法……
如果估出下一位的商等于或大于5……
小彤
都用“四舍五入”的方法。
小雅
根据实际情况或题目要求取近似数。
求商的近似数时,计算到比保留的小数位数多一位。
小伟
求商的近似数和求积的近似数,方法一样吗?
小亮
小飞
按要求,求商的近似数。
1 .5 5
3 .9
3
0
1 1 7
3 8
0
9 7
3 5 1
2 9 0
2 7 3
1 7
(1)结果保留一位小数
(2)结果保留两位小数
(3)结果保留三位小数
1.55÷3.9≈0.4
1.55÷3.9≈0.40
1.55÷3.9≈0.397
1.5 5 ÷ 3.9 ≈
?
0
4
1 5 6
1 4
4 0
小茹
小兰
一支铺路队正在铺一段公路。上午工作3.5小时,铺了164.9 m;下午工作4.5小时,铺了206.7 m。
明明
是上午铺路的速度快,
还是下午铺路的速度快?
写一写、算一算,选择合适的方法解决问题。
明明
是上午铺路的速度快,
还是下午铺路的速度快?
小刚
求商的近似数时,计算到比保留的小数位数多一位,再将最后一位“四舍五入”。
需要根据实际情况求近似数。
知识之间是有联系的。
小亮
通过这节课的学习,你们有什么收获?
老师
小彤
小勇
学
习
内
容
1.完成数学书第36页第1题。
2.完成数学书第37页第8题。
课
后
练
习
2.8 3
× 0.9
2.5 4 7
2.83×0.9
2.83×0.9 ≈ 2.5
4
2.83×0.9 ≈ 2.55
7
小飞
结果保留一位小数
结果保留两位小数
四舍五入
小彤
文文
什么时候需要求商的近似数?
求商的近似数和求积的近似数,方法一样吗?
小亮
资料
资料
这筒羽毛球19.86元。
一筒是12个。
小丁
每个羽毛球大约多少钱?
可以写一写、算一算,求出每个羽毛球大约多少钱?
小飞
商的近似数
小锐
芳芳
( )
1 9 . 8 6
1 2
1 2
7
7 2
6 6
1 . 6 5 5
6 0
6 0
6 0
0
8
19.86÷12 ≈
→向前一位进1
看小数部分第三位上的数,用“四舍五入”的方法……
保留两位小数
1.66(元)
小莹
1 9 . 8 6
1 2
1 2
7
7 2
6 6
1 . 6 5 5
6 0
6 0
6 0
0
8
19.86÷12 ≈
小亮
保留一位小数
看小数部分第二位上的数,用“四舍五入”的方法……
1.7(元)
文文
什么时候需要求商的近似数?
在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
优惠促销
羽毛球每筒12个,售价18.5元。
小涵
平均每个羽毛球大约多少钱?
请你算一算每个羽毛球大约多少钱?(保留两位小数)
小涵
平均每个羽毛球大约多少钱?
优惠促销
羽毛球每筒12个,售价18.5元。
18.5÷12 ≈ (保留两位小数)
小丁
必须算完才能求商的近似数吗?
小锐
小彤
舍
小亮
小涵
小锐
文文
18.5÷12 ≈ (保留两位小数)
( )
1.54(元)
(保留三位小数)
1.5 4 2
1 8 .5
1 2
1 2
6 5
6 0
5 0
1 .5 4 1 6
4 8
2 0
1 2
8 0
1 8.5 ÷ 1 2 ≈
7 2
8
小刚
保留三位小数,计算到小数部分第四位……
1 8 .5
1 2
1 2
6 5
6 0
5 0
1 .5 4 1 6 6
4 8
2 0
1 2
8 0
7 2
8 0
7 2
8
(保留四位小数)
1.5 4 1 7
小涵
保留四位小数,计算到小数部分第五位……
1 8.5 ÷ 1 2 ≈
求商的近似数时,计算到比保留的小数位数多一位,再将最后一位“四舍五入”。
小丁
说一说,怎样求商的近似数?
老师
小涵
保留四位小数,计算到小数部分第五位……
小刚
保留三位小数,计算到小数部分第四位……
小勇
小莹
没计算到小数部分第三位,怎么求近似数?
添“0”继续除,最多商“1”……
小勇
芳芳
估出下一位的商是几,就可以用“四舍五入”的方法……
如果估出下一位的商等于或大于5……
小彤
都用“四舍五入”的方法。
小雅
根据实际情况或题目要求取近似数。
求商的近似数时,计算到比保留的小数位数多一位。
小伟
求商的近似数和求积的近似数,方法一样吗?
小亮
小飞
按要求,求商的近似数。
1 .5 5
3 .9
3
0
1 1 7
3 8
0
9 7
3 5 1
2 9 0
2 7 3
1 7
(1)结果保留一位小数
(2)结果保留两位小数
(3)结果保留三位小数
1.55÷3.9≈0.4
1.55÷3.9≈0.40
1.55÷3.9≈0.397
1.5 5 ÷ 3.9 ≈
?
0
4
1 5 6
1 4
4 0
小茹
小兰
一支铺路队正在铺一段公路。上午工作3.5小时,铺了164.9 m;下午工作4.5小时,铺了206.7 m。
明明
是上午铺路的速度快,
还是下午铺路的速度快?
写一写、算一算,选择合适的方法解决问题。
明明
是上午铺路的速度快,
还是下午铺路的速度快?
小刚
求商的近似数时,计算到比保留的小数位数多一位,再将最后一位“四舍五入”。
需要根据实际情况求近似数。
知识之间是有联系的。
小亮
通过这节课的学习,你们有什么收获?
老师
小彤
小勇
学
习
内
容
1.完成数学书第36页第1题。
2.完成数学书第37页第8题。
课
后
练
习
