青岛(六三)版数学五上 智慧广场--排列 课件(22张ppt)
文档属性
| 名称 | 青岛(六三)版数学五上 智慧广场--排列 课件(22张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 13.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 21:36:25 | ||
图片预览


文档简介
排 列
一、情境导入
从图中,你知道了哪些数学信息?
小冬、小华、小平3个同学排成一行照相
有多少种不同的排法?
二、合作探索
有多少种不同的排法?
小冬
1.请同学们拿出预习单,自己动手写一写,数一数,你们能找到几种不同的排法?
小华
小平
2.把你的想法和排法在小组内交流一下。
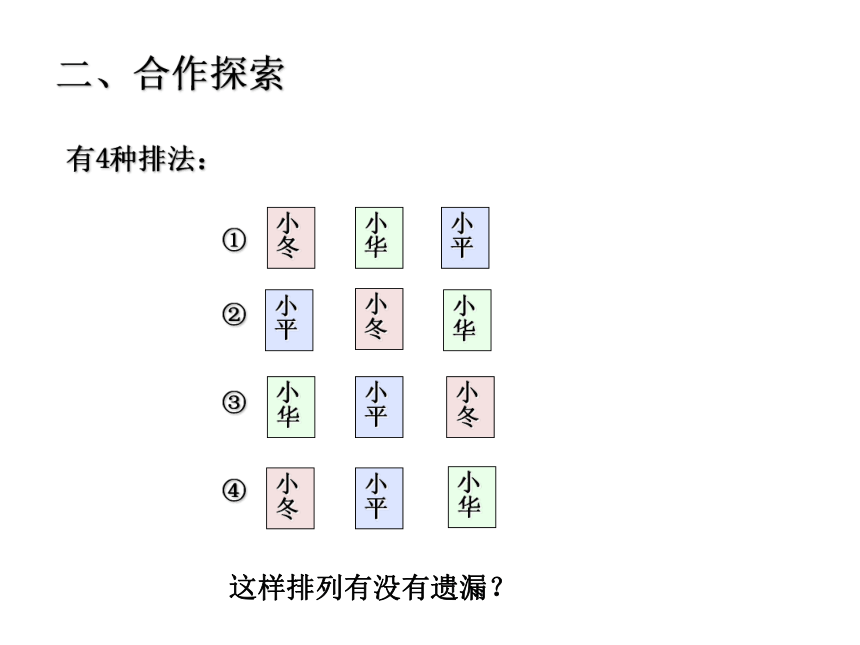
有4种排法:
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
二、合作探索
这样排列有没有遗漏?
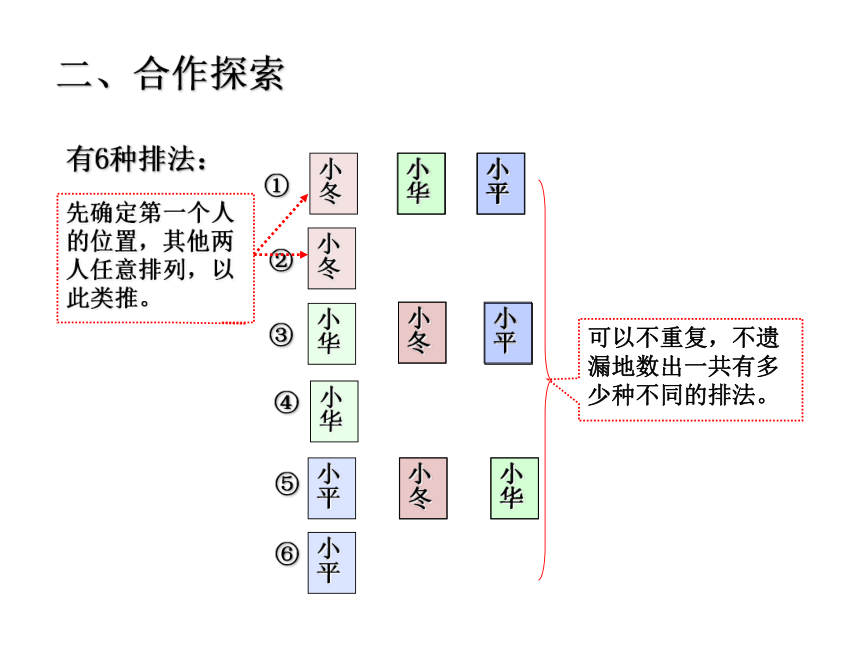
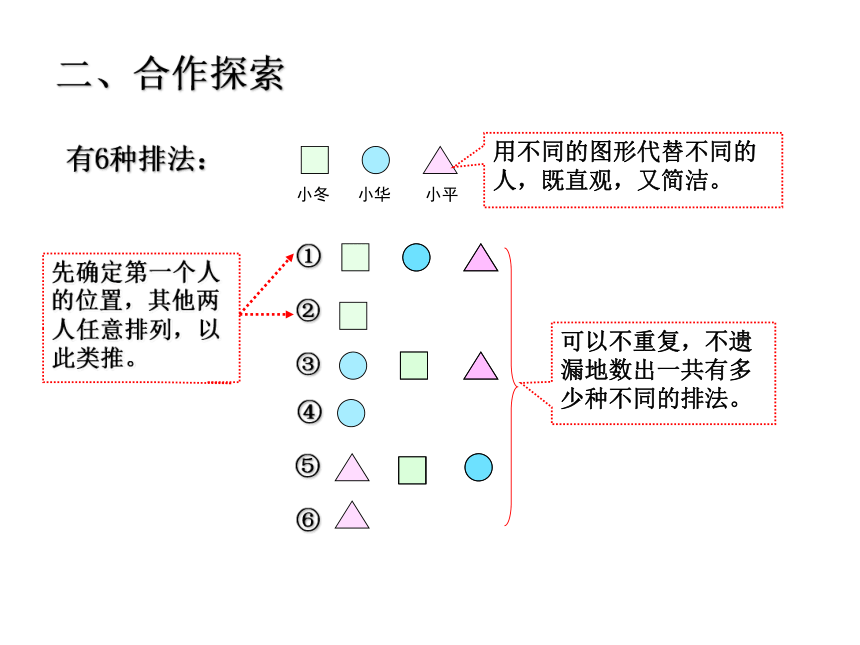
有6种排法:
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小平
小华
小冬
小华
小平
小冬
小平
小冬
小华
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
有6种排法:
小冬
小华
小平
①
②
③
④
⑤
⑥
用不同的图形代替不同的人,既直观,又简洁。
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
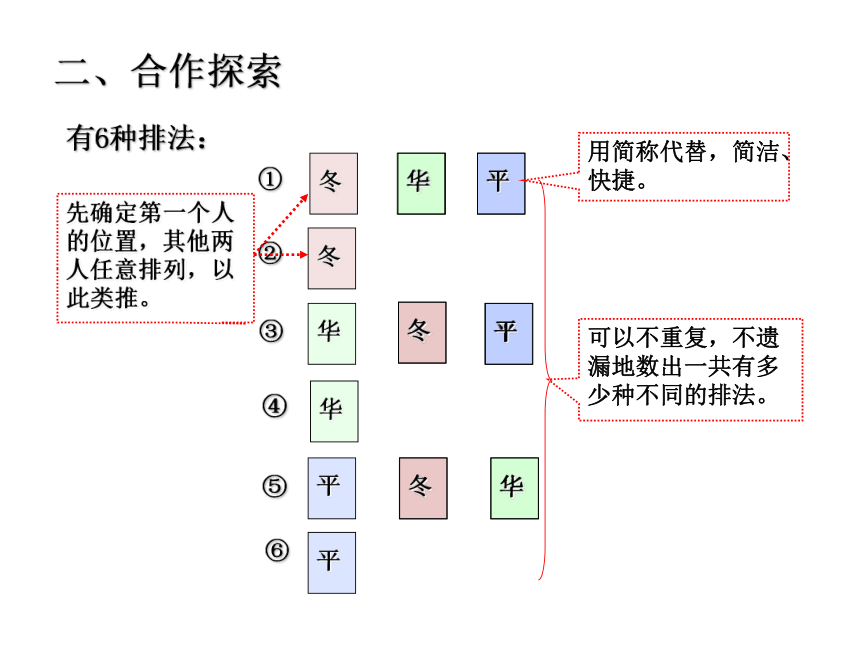
有6种排法:
冬
华
平
冬
华
平
华
平
冬
平
华
冬
华
平
冬
平
冬
华
用简称代替,简洁、快捷。
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
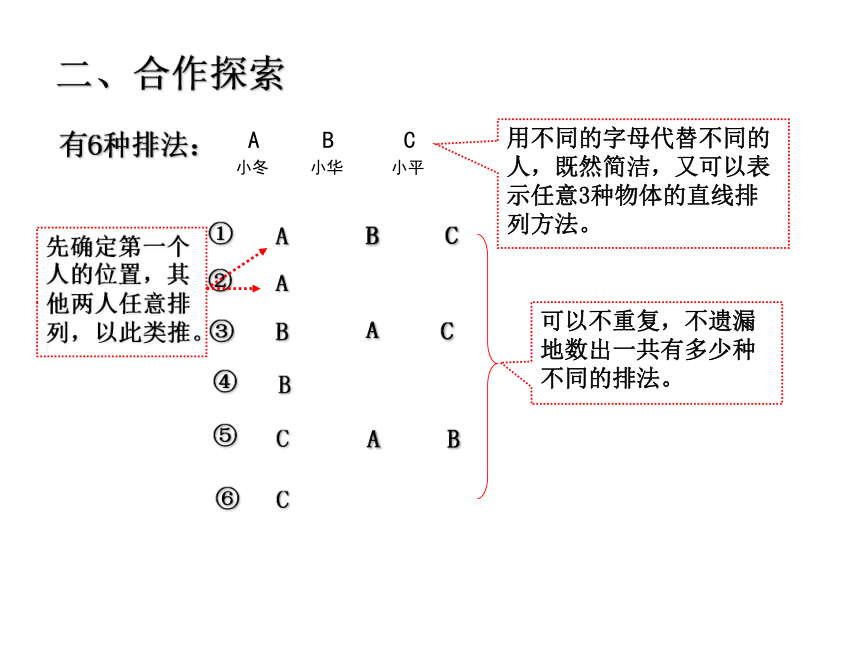
有6种排法:
A
B
C
A
B
C
B
C
A
C
B
A
B
C
A
C
A
B
①
②
③
④
⑤
⑥
用不同的字母代替不同的人,既然简洁,又可以表示任意3种物体的直线排列方法。
小冬
A
小华
B
小平
C
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
二、合作探索
先确定第一个人的位置,其他两人自由排列,数出有
几种排列方法,依次类推,这样可以不重复、不遗漏地数
出一共有多少种排法。
4.你知道吗?
三、自主练习
4.你知道吗?
三、自主练习
4.你知道吗?
三、自主练习
4.你知道吗?
三、自主练习
1.三个同学排成一行跳舞,可以有多少种不同的排法?
答:可以有6种不同的排法。
三、自主练习
小云 小雪 小雨
小云 小雨 小雪
①
②
小雨 小云 小雪
小雨 小雪 小云
③
④
小雪 小雨 小云
小雪 小云 小雨
⑤
⑥
三、自主练习
2、用下面的文字卡片,你能摆出多少个由3个字组成的短句?
龙
虎
斗
龙虎斗、龙斗虎、虎龙斗、虎斗龙、斗龙虎、斗虎龙。
答:有6种不同摆法。
三、解决问题。(“智慧大闯关”第一关)
要在酒店的大门上方挂6只大灯笼,如果把形状相同的挨在一起,可以有几种不同的挂法?
6只灯笼只有3种形状,挂6只灯笼和挂3只灯笼的思路是一样的。
2.四位同学排一行表演小合唱,王刚同学担任领唱。固定在左起第二个位置上,其余同学任意排。有多少种不同的排法?
试一试
D
D
D
D
D
A
三、自主练习
2.五年一班在筹划参加校运动会接力赛方案时,决定让本班短跑速度最快的王明同学跑第四棒,其余三位同学李华、张强、丁力跑其它三棒。可以有多少种不同的安排方法?
A
李华
B
张强
C
丁力
D
王明
C
③
④
⑤
⑥
A
B
C
B
D
①
②
C
A
B
A
C
B
B
C
C
A
A
B
排列组合问题,最早见于我
国的《易经》一书,书中记载了
与占卜有关的八卦算。即把卦按
不同的方法在8个方位中排列起
来。如今,排列组合问题已经成
为一门学问,引起了人们的广泛
关注和研究。
你知道吗?
三、自主练习
0
3.用0—3四个数字可以组成多少个不同的四位数?(每个数字只用一次)
1023 1032 1203 1230 1302 1320
2013 2031 2103 2130 2301 2310
3012 3021 3102 3120 3201 3210
6个
6个
6个
1
2
3
答:可以组成18个不同的四位数。
四、回顾反思
一、情境导入
从图中,你知道了哪些数学信息?
小冬、小华、小平3个同学排成一行照相
有多少种不同的排法?
二、合作探索
有多少种不同的排法?
小冬
1.请同学们拿出预习单,自己动手写一写,数一数,你们能找到几种不同的排法?
小华
小平
2.把你的想法和排法在小组内交流一下。
有4种排法:
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
二、合作探索
这样排列有没有遗漏?
有6种排法:
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小平
小华
小冬
小华
小平
小冬
小平
小冬
小华
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
有6种排法:
小冬
小华
小平
①
②
③
④
⑤
⑥
用不同的图形代替不同的人,既直观,又简洁。
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
有6种排法:
冬
华
平
冬
华
平
华
平
冬
平
华
冬
华
平
冬
平
冬
华
用简称代替,简洁、快捷。
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
有6种排法:
A
B
C
A
B
C
B
C
A
C
B
A
B
C
A
C
A
B
①
②
③
④
⑤
⑥
用不同的字母代替不同的人,既然简洁,又可以表示任意3种物体的直线排列方法。
小冬
A
小华
B
小平
C
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
二、合作探索
二、合作探索
先确定第一个人的位置,其他两人自由排列,数出有
几种排列方法,依次类推,这样可以不重复、不遗漏地数
出一共有多少种排法。
4.你知道吗?
三、自主练习
4.你知道吗?
三、自主练习
4.你知道吗?
三、自主练习
4.你知道吗?
三、自主练习
1.三个同学排成一行跳舞,可以有多少种不同的排法?
答:可以有6种不同的排法。
三、自主练习
小云 小雪 小雨
小云 小雨 小雪
①
②
小雨 小云 小雪
小雨 小雪 小云
③
④
小雪 小雨 小云
小雪 小云 小雨
⑤
⑥
三、自主练习
2、用下面的文字卡片,你能摆出多少个由3个字组成的短句?
龙
虎
斗
龙虎斗、龙斗虎、虎龙斗、虎斗龙、斗龙虎、斗虎龙。
答:有6种不同摆法。
三、解决问题。(“智慧大闯关”第一关)
要在酒店的大门上方挂6只大灯笼,如果把形状相同的挨在一起,可以有几种不同的挂法?
6只灯笼只有3种形状,挂6只灯笼和挂3只灯笼的思路是一样的。
2.四位同学排一行表演小合唱,王刚同学担任领唱。固定在左起第二个位置上,其余同学任意排。有多少种不同的排法?
试一试
D
D
D
D
D
A
三、自主练习
2.五年一班在筹划参加校运动会接力赛方案时,决定让本班短跑速度最快的王明同学跑第四棒,其余三位同学李华、张强、丁力跑其它三棒。可以有多少种不同的安排方法?
A
李华
B
张强
C
丁力
D
王明
C
③
④
⑤
⑥
A
B
C
B
D
①
②
C
A
B
A
C
B
B
C
C
A
A
B
排列组合问题,最早见于我
国的《易经》一书,书中记载了
与占卜有关的八卦算。即把卦按
不同的方法在8个方位中排列起
来。如今,排列组合问题已经成
为一门学问,引起了人们的广泛
关注和研究。
你知道吗?
三、自主练习
0
3.用0—3四个数字可以组成多少个不同的四位数?(每个数字只用一次)
1023 1032 1203 1230 1302 1320
2013 2031 2103 2130 2301 2310
3012 3021 3102 3120 3201 3210
6个
6个
6个
1
2
3
答:可以组成18个不同的四位数。
四、回顾反思
